-33-

Раздел 3 элементы аналитической геометрии

Глава 5. Координаты точки. Прямая линия

5.1. Метод координат. Простейшие задачи аналитической геометрии

В основе аналитической геометрии лежит метод координат, впервые систематически примененный французским математиком и философом Декартом. Простейшая и наиболее употребительная система координат на плоскости представляет собой две взаимно перпендикулярные оси с заданными единичными отрезками для измерения длин. Точка пересечения осей называется началом координат (обозначается буквой O), сами оси – координатными осями, горизонтальная ось называется осью абсцисс (обозначается Ox), вертикальная – осью ординат (обозначается Oy). Пусть М – произвольная точка плоскости. Проведем через эту точку перпендикуляры к прямым Ox и Oy; основания перпендикуляров обозначим M_x и M_y (рис. 5.1). Координатами точки М в заданной системе называются числа x = M_x, y = M_y. Вставка рис. 5.1

Каждой точке М ставится в соответствие упорядоченная пара чисел ; каждой паре чисел соответствует точка плоскости. Любая геометрическая задача благодаря этому может быть сведена к задаче алгебраической, при этом сохраняется наглядность благодаря геометрическим построениям..

Рассмотрим две простейшие задачи аналитической гео­метрии.

Задача 1. Даны две точки и (рис. 5.2). Найдем расстояние меж­ду ними.

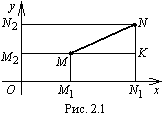
Из точек М и N опустим перпендикуляры , , и на оси ко­ординат. Здесь , , , . Проведем отрезок МК, параллельный оси Ох.

Рассмотрим прямоугольный треугольник MNK. По теореме Пифагора имеем

.

Выразим отрезки МК и NK через координаты данных точек.

Следовательно,

,

или

.

(5.1)

Пример 5.1. Даны точки , . Найти расстояние АВ.

Используя (5.1), получаем

.

Задача 2. Даны две точки и , являющиеся концами отрезка, и число λ. Требуется найти координаты точки S, такой, что

,

т.е. разделить отрезок в данном отношении λ (рис. 5.3).

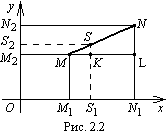
Обозначим через координаты точки S. Из точек N, S и М опустим перпендикуляры на оси Ох и Оy.

Проведем отрезок МL параллель­ный оси Ох. Он пересекается с отрезком в точке К. Рассмотрим угол . Параллельные прямые SK и NL отсекают на нем пропорциональные отрезки. Следовательно,

.

(5.2)

Выразим отрезки МК и KL через координаты точек:

Подставляя в равенство (5.2) выражения МК и KL, получаем

или

Откуда

.

(5.3)

Аналогично доказывается, что

.

(5.4)

Рассмотрим частный случай – деление отрезка по­полам, т.е. требуется найти точку S, такую, что MS = NS. В этом случае

.

Подставляя в (5.3), (5.4), получаем искомые формулы

.

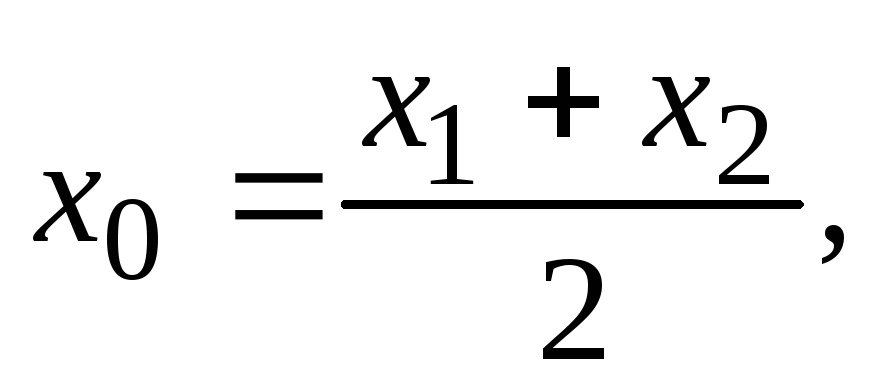
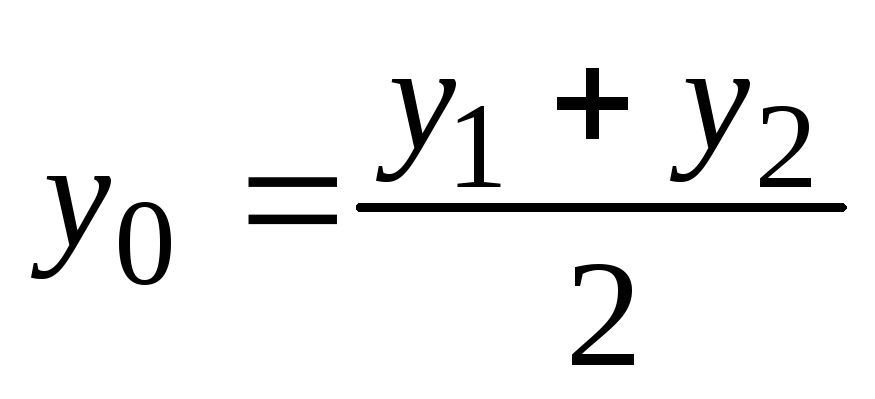(5.5)

Пример 5.2. Дан треугольник с вершинами , , . Найти координаты точки P – центра тяжести тре­угольника. Известно, что в точке P пересекаются медианы (рис. 5.4). Поэтому проведем

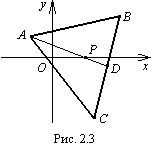
медиану AD, где точка D – середина отрезка ВС. По формулам (5.5) находим ее координаты.

,

т.е. D(5; –1).

Рассмотрим отрезок AD. Точка P, по свойству медианы, делит его так, что

.

Найдем координаты точки Р:

.

Точка Р имеет координаты .