лабораторная работа / lr5

БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ.

ФАКУЛЬТЕТ ИНЖЕНЕРНО- СТРОИТЕЛЬНЫЙ.

КАФЕДРА УПРАВЛЕНИЕ И ИНФОРМАТИКА В ТЕХНИЧЕСКИХ СИСТЕМАХ.

ЛАБОРАТОРНАЯ РАБОТА №5

ПО курсу ТАУ

Метод гармонической линеаризации

Вариант 7

Выполнил студент гр. УИТ-43

Колесников И. А.

Принял

Мефедова Ю. А.

2004

Цель работы: Изучение нелинейных систем с помощью метода гармонической линеаризации (гармонического баланса), определение коэффициентов гармонической линеаризации для различных нелинейных звеньев. Получение навыков по нахождению параметров симметричных колебаний постоянной амплитуды и частоты (автоколебаний), используя алгебраический, частотный способы, а также с помощью критерия Михайлова.

1. Для нелинейной характеристики, вид которой (нелинейная характеристика с зоной насыщения без зоны нечувствительности)

С переменным коэффициентом усиления

b=0.1 k1=0.5 k2=0.4 рассчитать коэффициенты гармонической линеаризации.

Из графика следует

.

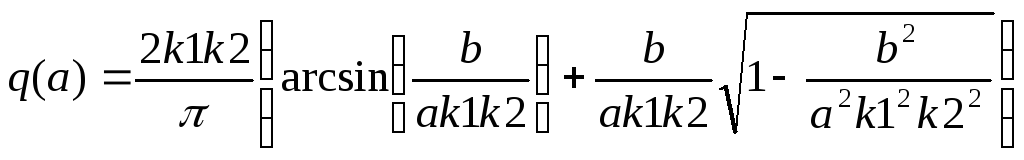
2. Определить параметры автоколебаний для системы, представленной на рис. 4. при этом релейная характеристика нелинейного элемента из пункта 1, параметры системы – из таблицы 2, согласно номеру варианта.

Таблица 2.

k (1/сек)	T1(сек)	T2(сек)
7	0,1	0,25

нелинейная система имеет вид

Рис.4

2.1 Амплитуда и частота автоколебаний для исследуемой системы определим алгебраическим способом .

У нас нелинейный элемент имеет вид из пункта 1 для которого коэффициенты гармонической линеаризации

.

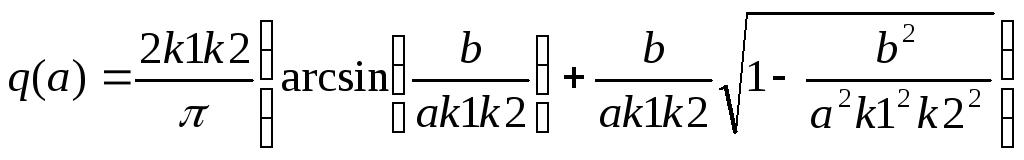
Исполнительное устройство имеет передаточную функцию вида

.

Передаточная функция объекта регулирования равна

.

Передаточная функция линейной части системы

,

где .

запишем характеристическое уравнение замкнутой системы

Откуда

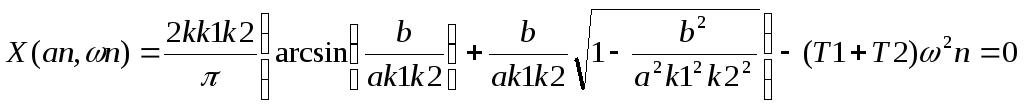
В этом случае параметры периодического движения равны

6.324 ,

an найдем графически

2.2 Нахождение параметров автоколебаний с помощью критерия Михайлова.

Линейная часть осталась неизменной.

коэффициенты гармонической линеаризации те же

Запишем характеристическое уравнение замкнутой системы

Годограф Михайлова получается заменой .

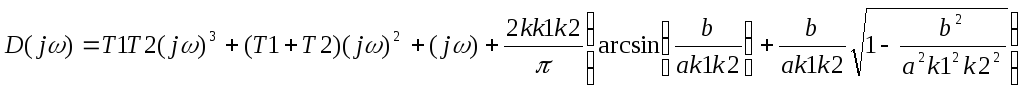
2.3 Применение частотного способа.

Запишем частотную передаточную функцию разомкнутой системы

.

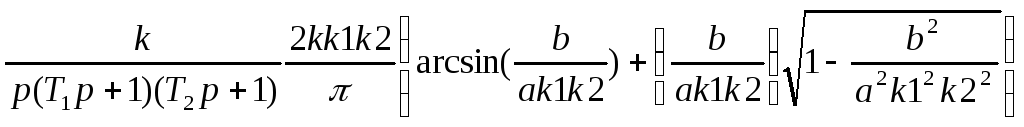Используем иной подход к определению периодического решения. Запишем условие возникновения колебаний

,

или

.

Согласно критерию Найквиста в замкнутой системе возникнут колебания, если амплитудно-фазовая частотная характеристика разомкнутой системы пройдет через точку (-1, j0). По графику видно, что у нас нету пересечения, следовательно, в системе нет колебаний.