Министерство образования и науки Российской федерации

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Факультет кибернетики

Кафедра вычислительной техники

Лабораторная работа №2 по дисциплине теория управления систем

Исследование свойств звена при охвате его обратной связью

наименование темы

Выполнил: студент гр. АСУз-08-1

Гурин Константин Викторович

Проверил преподаватель:

Маланова Татьяна Валерьевна

г. Иркутск @

Содержание.

ЗАДАНИЕ 3

Изложение метода моделирования W(p) 3

Исследование W(p) обратной связью 4

1. В жестком отрицательном режиме 4

2. В жестком положительном режиме 4

Соображения значения шага интегрирования и величины интервала интегрирования L 5

3. Листинг фрагмента программы, относящегося к моделированию исследуемой автоматической системы. 5

5

ЗАДАНИЕ

1.Рассмотреть отрицательную обратную связь. Показать аналитически, как изменяются характер и параметры звена W(p) в диапазоне возможного изменения коэффициента обратной связи

2.Рассмотреть отрицательную обратную связь. Вычислив корни характеристического уравнения замкнутой автоматической системы исследовать её устойчивость в диапазоне возможного изменения коэффициента обратной связи

3.Выводы предыдущих пунктов 1 и 2 проиллюстрировать путем моделирования.

4.Рассмотреть положительную обратную связь. Показать аналитически, как изменяются характер и параметры звена W(p) в диапазоне возможного изменения коэффициента обратной связи

5.Рассмотреть положительную обратную связь. Вычислив корни характеристического уравнения замкнутой автоматической системы исследовать её устойчивость в диапазоне изменения коэффициента обратной связи

6.Выводы предыдущих пунктов 4 и 5 проиллюстрировать путем моделирования.

Вариант 17

№	Вид	k	T		T1	T2	Вид обратной связи
17	Инерционное	0,1	10				Жесткая ОС

Изложение метода моделирования W(p)

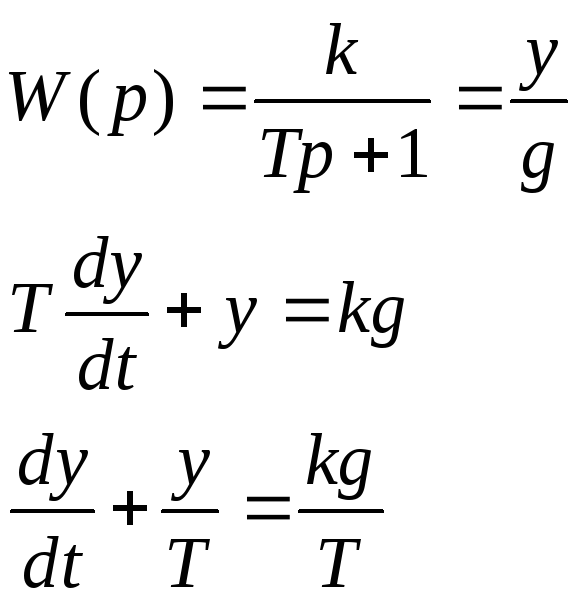
n=1, m=1

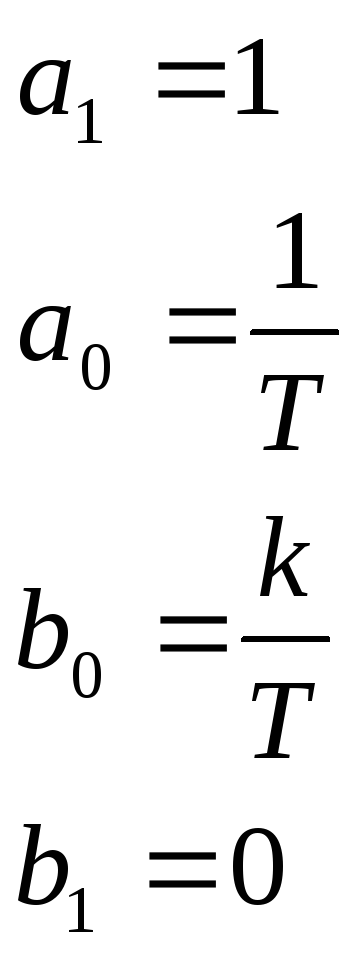
Исследование W(p) обратной связью

1. В жестком отрицательном режиме

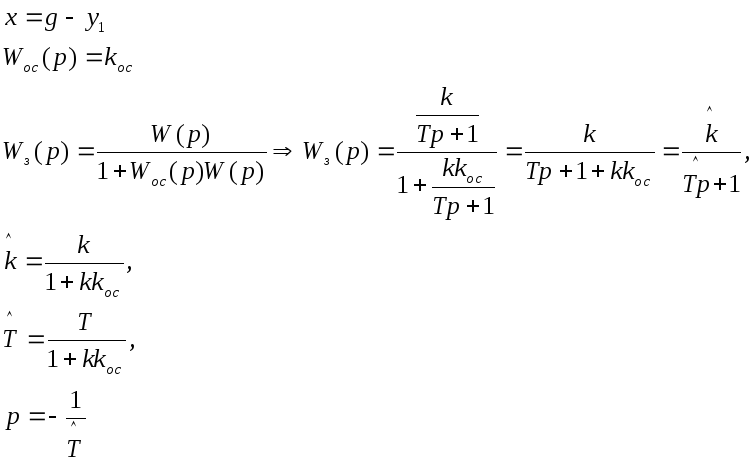
При охвате инерционного звена жесткой отрицательной обратной связью его устойчивость не нарушается.

2. В жестком положительном режиме

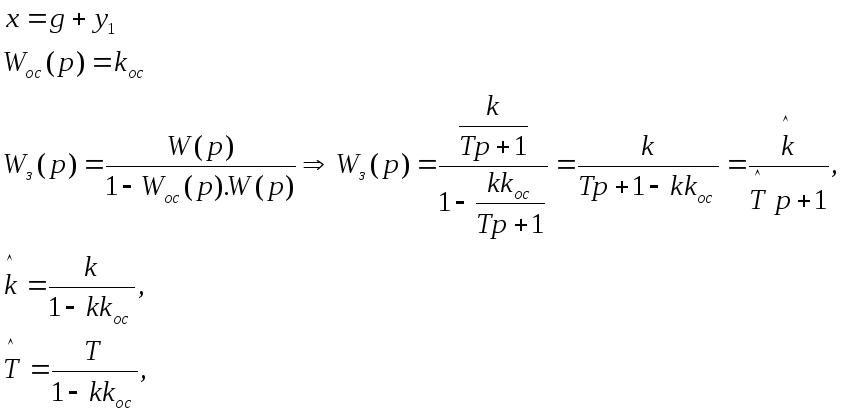
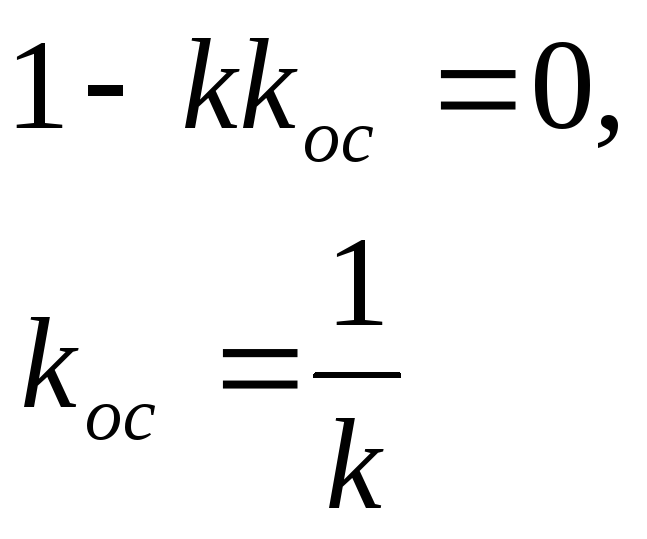
, находится на границе устойчивости.

При , система устойчива.

При , система неустойчива.

Соображения значения шага интегрирования и величины интервала интегрирования L

Приближенно интервал интегрирования можно оценить: в звеньях первого порядка

Тогда

3. Листинг фрагмента программы, относящегося к моделированию исследуемой автоматической системы.

function f0 (x,y:real):real;

begin

result:=(x*k-y)/T;

end;

function hh(dt:real):real;

begin

result:=k*(1-exp(-dt/T));

end;

procedure TForm1.Button4Click(Sender: TObject);

var

x,dy,y,dt:real; i,znak:integer;

begin

dt:=0; y:=0;

Series1.clear;

Series2.clear;

if Edit1.text= '' then MessageDlg('Введите Кос', mtError, [mbOk], 0) else

begin

Koc:= StrToFloat(Edit1.text);

Chart1.Title.Text.clear;

Chart1.Title.Text.add('Графики, полученные при моделировании');

if RadioButton2.Checked=true then

znak:=-1 else znak:=1;

repeat

x:=1+znak*y*Koc;

for i:=1 to n do

k1[i]:=0; dy:=0;

k1[1]:=h*f0(x,y);

k1[2]:=h*f0(x,y+k1[1]/2);

k1[3]:=h*f0(x,y+k1[2]/2);

k1[4]:=h*f0(x,y+k1[3]);

dy:=(k1[1]+2*(k1[2]+k1[3])+k1[4])/6;

y:=y+dy;

Series1.addXY(dt,hh(dt),'',clteecolor);

Series2.AddXY(dt,y, '',clteecolor);

dt:=dt+h

until dt>L;

end;

end;

4. Графики, полученные путем моделирования.

На графике видим, что в случае отрицательной обратной связи при заданных параметрах k=1; T=10, получаем, что То есть . И , то есть . Система с отрицательной обратной связью обладает устойчивостью.

Пусть Кос =0,5 при положительной обратной связи:

На графике видим, что в случае положительной обратной связи при заданных параметрах k=1; T=10, в случае получаем, что то есть . И , то есть , Система с положительной обратной связью обладает устойчивостью.

Пусть Кос=2 при положительной обратной связи:

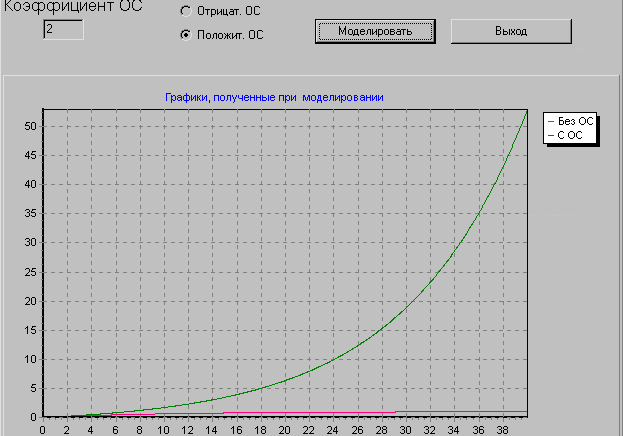
На графике видим, что в случае положительной обратной связи при заданных параметрах k=1; T=10, в случае получаем, что и , Система с положительной обратной связью не обладает устойчивостью.

Пусть Кос=1 при положительной обратной связи

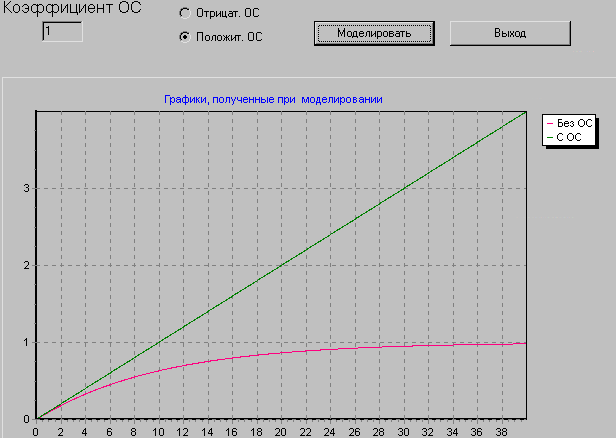
При система находится на границе устойчивости.

1