
шпоргалка / shpory_po_tau
.doc|
1 Автоматическая система управления - автоматическая система с замкнутой цепью воздействий, в которой управляющие воздействия вырабатываются в результате сравнения действительных значений управляемой величины с предписанными значениями. Элементарное звено - искусственно выделяемая часть автоматической системы, соответствующая какому-нибудь элементарному алгоритму. Динамическое звено - элементарное звено, осуществляющее изменение функциональной зависимости воздействия, подаваемого на вход звена, во времени. Передаточная функция – изображение по Лапласу отношения выходной величины по входной при нулевых начальных условиях.
Система регулирования называется статической по отношению к возмущающему (управляющему) воздействию, если при воздействии стремящемся к установившемуся постоянному значению, отклонение регулируемой величины также стремится к постоянному значению, зависящему от величины воздействия. Статической системе присуща статическая (установившаяся) ошибка. Автоматическая система называется астатической по отношению к возмущающему (управляющему) воздействию, если при воздействии стремящемся к некоторому установившемуся постоянному значению отклонение регулируемой функции стремится к нулю вне зависимости от величины воздействия. Одна и та же система может быть статической по отношению к возмущающему воздействию и астатической по отношению к управляющему воздействию. Астатические системы могут быть I–го и более высокого порядков. Функциональная схема - каждому функциональному элементу системы соответствует определенное звено. Структурная схема - каждой математической операции преобразования сигнала соответствует определённое звено. |
2
1 – система устойчивая 2 – система на границе устойчивости 3 – система неустойчивая А
Ф |
3. Последовательное W Параллельное W Встречно-параллельное
|
Дифференцирующее звено И Р 1) Цепь разряда конденсатора
2 |
||||||||||||
|
4. Безинерционное (пропорциональное звено)
Апериодическое звено (инерционное первого порядка)
Апериодическое звено вносит фазовые изменения в выходном сигнале относительно входного.
|
7. Входные воздействия С
Если система устойчива, то при подаче возмущающего воздействия на вход системы, она приходит в состояние равновесия через некоторое время. По графику переходного процесса можно увидеть устойчивая или неустойчивая система. Если переходный процесс протекает с колебаниями затухающего виду, то система устойчивая. Если переходный процесс представляет собой незатухающие гармонические колебания с постоянной амплитудой, то система на границе устойчивости. Если переходный процесс представляет собой колебания с постоянно увеличивающейся амплитудой, то система неустойчивая. Если график переходного процесса через некоторое время приходит к определенному значению (не важно как приходит), то система устойчивая. Если же график переходного процесса не приходит к определенному значению (т.е. исследуемая величина изменяется во времени), то система неустойчивая.
|
|
8. Передаточная характеристика замкнутой системы по заданному контуру Для анализа и синтеза систем надо знать: уравнение статики, динамики и передаточную функцию. Один из методов получения этих уравнений – структурный метод. Он заключается в том, что на основании алгоритмической схемы системы по определенным правилам записывают передаточную функцию системы, а затем уравнение статики и динамики. Для того чтобы записать передаточную ф-ию замкнутой системы, необходимо преобразовать структуру всей системы (прямой и обратной цепи) в последовательном соединении эквивалентных передаточных функций. Передаточная ф-ия замкнутой системы записывается в виде дроби, в числителе которой передаточная ф-ия прямого канала м-у местом приложения воздействия и местом съема сигнала. А в знаменателе 1±произведение эквивалентных передаточных ф-ий, образующих замкнутый контур. Канал Хз-Х – канал системы по задающему воздействию относительно управляемой величины. Z-X – по возмущению относительно управляемой величины. Хз-ε – канал ошибки. Передаточные ф-ии замкнутой системы по различным каналам необходимы для мат. анализа реакции системы на разл. воздействия. Уравнение статики системы - составляется путем перемножения передаточной функции замкнутой системы по определенному контуру на воздействие этого контура. |
9. П-регулятор W +простота реализации +быстродействие -малая точность в установившемся режиме Не применяется в астатических системах И-регулятор W +высокая точность в установившемся режиме -высокая колебательность в переходном режиме ПИ-регулятор W(p)=kp+ku/p, ku=Kp/Tu, кр=Roc/R1, R2=R3, R5=R4=R6 +высокая точность в установившемся режиме +при правильном подборе kp и Tu хороший переходный процесс +наиболее распространенный закон Самый гибкий закон регулирования
|
10. Если точность системы хар-ет эффективность работы системы, то устойчивость хар-ет её работоспособность. Если система неустойчива -> она неработоспособна. Устойчивость – приведение системы в исходное состояние равновесия после прекращения воздействия, выведшего её из исходного состояния. Устойчивость системы зависит только от элементов, входящих в неё и не зависит от величины воздействия. Существует несколько критериев определения устойчивости системы: Гурвица, Михайлова, Найквиста, логарифмический. Δ ΔL – запас по амплитуде (при достижении фазовой хар-ой -180˚) Рекомендуемые запасы устойчивости: по фазе 20..30˚, по амплитуде не менее 7дБ. Алгебраический
критерий устойчивости Гурвица.
«Система, описываемая характеристическим
уравнением вида
|
1 1 – система устойчива 2 – система на границе устойчивости 3 – система неустойчива Г
1 – система устойчивая 2 – система на границе устойчивости 3 – система неустойчивая
Ф |
|
1 Статическая точность – точность, с которой система отрабатывает входное задающее воздействие (ошибка системы в установившемся режиме) Динамическая точность – параметры переходного процесса, которым должна соответствовать система в соответствии с заданием (σ – перерегулирование, tn– время переходного процесса,М-колебательность)
|
|
13. Нелинейные САУ – содержат в себе хотя бы один нелинейный элемент (эл-т с нелинейной статической хар-ой) а б – двухпозиционный регулятор в – трехпозиционный регулятор г – хар-ка с зоной ограничения д – гестерезисная релейная хар-ка е – зона нечувствительности и ограничения Нелинейные элементы бывают статические и динамические (д). Нелинейные эл-ты в САУ бывают естественными и искусственными. Естественные нелинейности – это эл-ты системы, обязательно входящие в неё (часто это рабочие органы – задвижки, вентили), объекты управления с зоной насыщения, исполнительные механизмы с ограниченным диапазоном, разл. механические передачи. Искусственные нелинейности – эл-ты, преднамеренно введенные в систему для улучшения качества управления (двухпоз. и трехпоз. регуляторы). Они обеспечивают быстродействие системы, простоту реализации закона регулирования, экономичность и надежность. *Хар-р переходного процесса зависит от величины входного воздействия (при малых воздействиях система устойчива, а при больших может выходить из состояния устойчивости) *Могут работать в режиме автоколебаний (колебания выходной величины с постоянной амлитудой и частотой). Такой режим работы не явл-ся неустойчивым. Сущ-ют нелинейные СУ, постоянно работающие в таком режиме. Для них этот режим является рабочим и их трудно вывести из этого состояния. Д
|
14. ДПТ как объект управления
Д |
17. Программно-технический комплекс С Полевой уровень содержит устройства, расположенные непосредственно на объекте (дачтика, ИМ, рабочие органы, исполнительные двигатели). PLC-промежуточный уровень. На этом уровне осуществляется управление по заданным алгоритмам и законам, а т.ж. сбор информации и её первичное преобразование с полевого уровня.SCADA(АСУТП)-авт. система управления технологическим процессом. Ф-ии уровня: сбор информации с нижних уровней, хранение информации, диспетчеризация информации, предоставление возможности оператору дистанционного управления процессом, алармирование. Информация на этом уровне представлена в виде мнемосхемы на ЭВМ оператора. MES(АСУПП)-авт. система управления производственным процессом. Ф-ии: расчет технико-экономических показателей производственного процесса. На этом уровне осуществляется планирование производства. Контрольные периоды – час, смена, неделя… ERP(АСУП)-авт. система управления предприятием. Включает комплекс ПО для менеджеров и бухгалтеров. |
|
|
15. Система двухзонного регулирования ДПТ Частоту вращения ДПТ можно регулировать 2-я способами: 1 – изменяя U якоря 2 – изменяя магнитный поток обмотки возбуждения Система двухзонного регулирования предназначена для изменения ω как в сторону уменьшения, так и повышения. Регулирование ω по данной схеме осущ-ся с помощью двух независимых контуров управления. 1 конутр управления ω в сторону понижения включает в себя контур тока якоря и контур скорости. 2 для регулирования ω в сторону повышения исп-ся контур Твозб. Р
|
16. Применение современных технологий в системах автоматизации и управления технологическими процессами и производствами Для того, чтобы создать современную АСУТП, необходимо использовать современные технологии для сбора, передачи, отображения, регистрации, хранения и обработки информации. 1. Современные средства полевого уровня -современные датчики, ИМ, РО. Требования: точность измерения, унифицированный выходной сигнал (стандартные протоколы FieldBus), удобство монтажа и обслуживания, точность позиционирования, высокая надежность -управляющие устройства. Требования: точность реализации алгоритма управления, возможность управления несколькими контурами (одновременно), простота программирования, поддержка стандартных протоколов, возможность фильтрации и эффективного очищения от помех полезного сигнала -современные ср-ва отображения и диспетчеризации информации. Требования: надежность, удобство, эргономичность -эффективные ср-ва хранения и обр-ки информации. Требования: надежность аппаратных и программных средств. |

 ЧХ
– отражает усилительные и ослабляющие
свойства звеньев и систем.
ЧХ
– отражает усилительные и ослабляющие
свойства звеньев и систем. ЧХ
–
характеристика, отражающая изменение
фазы в зависимости от частоты в системе
или отдельном блоке. Построение:
выражение
фазы можно получить способом подставления
в передаточную ф-ию jω.
Получаем W(jω)=…
Получаем φ(ω)=arctg(aj+b)±…=arctg(a/b)±…
Составляем таблицу значений ω
и φ(ω).
По точкам строим график. Логарифмический
критерий устойчивости
– замкнутая система будет устойчивой,
если ЛАЧХ разомкнутого контура системы
пересекает ось частот в точке ωср
раньше, чем фазовая хар-ка разомкнутого
контура пересечет значение фазы -180˚.
ЧХ
–
характеристика, отражающая изменение
фазы в зависимости от частоты в системе
или отдельном блоке. Построение:
выражение
фазы можно получить способом подставления
в передаточную ф-ию jω.
Получаем W(jω)=…
Получаем φ(ω)=arctg(aj+b)±…=arctg(a/b)±…
Составляем таблицу значений ω
и φ(ω).
По точкам строим график. Логарифмический
критерий устойчивости
– замкнутая система будет устойчивой,
если ЛАЧХ разомкнутого контура системы
пересекает ось частот в точке ωср
раньше, чем фазовая хар-ка разомкнутого
контура пересечет значение фазы -180˚. экв=W1(p)+
W2(p)+…+
Wn(p)=
экв=W1(p)+
W2(p)+…+
Wn(p)=
 деальное
дифференцирующее звено – дельта-функция
(σ(t)).
Но такая функция в природе отсутствует.
Однако можно найти формальное
соотношение между входом и выходом
некоторых элементов, одним из них
является тахогенератор. Это прибор
«электрическая машина» для измерения
скорости вращения валов двигателя и
механизмов. Вал двигателя жестко
соединен с валом тахогенератора. На
выходе тахогенератора создается
напряжение, пропорциональное скорости
вращения вала. Если рассматривать ТГ
в небольшом промежутке времени, то
можно формально назвать его
дифференцирующим звеном, т.к. на его
выходе в небольшой промежуток времени
возникает импульсное напряжение.
Идеальное дифференцирующее звено
создает в системе положительный
фазовый сдвиг на π/2.
деальное
дифференцирующее звено – дельта-функция
(σ(t)).
Но такая функция в природе отсутствует.
Однако можно найти формальное
соотношение между входом и выходом
некоторых элементов, одним из них
является тахогенератор. Это прибор
«электрическая машина» для измерения
скорости вращения валов двигателя и
механизмов. Вал двигателя жестко
соединен с валом тахогенератора. На
выходе тахогенератора создается
напряжение, пропорциональное скорости
вращения вала. Если рассматривать ТГ
в небольшом промежутке времени, то
можно формально назвать его
дифференцирующим звеном, т.к. на его
выходе в небольшой промежуток времени
возникает импульсное напряжение.
Идеальное дифференцирующее звено
создает в системе положительный
фазовый сдвиг на π/2.
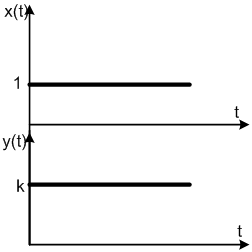



 (p)=kи/p,
kи=
Roc/R1
(p)=kи/p,
kи=
Roc/R1

 ПИД-регулятор
ПИД-регулятор

 φ
– запас
по фазе
φ
– запас
по фазе 1.
Частотный
критерий устойчивости
Михайлова.
Критерий основан на анализе
характеристического уравнения системы
и применяется для определения
устоцчивости разомкнутых и замкнутых
систем. Построение:
1) Записываем хар-ое ур-ие системы
1.
Частотный
критерий устойчивости
Михайлова.
Критерий основан на анализе
характеристического уравнения системы
и применяется для определения
устоцчивости разомкнутых и замкнутых
систем. Построение:
1) Записываем хар-ое ур-ие системы
 одограф
Найквиста
– графический критерий определения
устойчивости системы. Основан на
анализе АФЧХ разомкнутого контура
системы. «Замкнутая система управления
будет устойчивой, если АФЧХ разомкнутой
системы при изменении частот от 0 до
∞ не охватывает точку (-1;j0)»
Построение:
1)
Записать передаточную ф-ию разомкнутого
контура (пр-ие всех передаточных ф-ий,
входящих в замкнутый контур) 2) Раскрыть
скобки и привести подобные 3) Сгруппировать
коэфф-ты числителя и знаменателя по
четным и нечетным степеням при Р. 4)
Заменить операторы Лапласа Р на jω.
5) Сгруппировать коэфф-ты с j
и без j,
т.е. разбить на действительную и мнимую
части. 6) Записать выражения P(ω)=…
и Q(ω)=…
7) Составить таблицу значений, построить
график.
одограф
Найквиста
– графический критерий определения
устойчивости системы. Основан на
анализе АФЧХ разомкнутого контура
системы. «Замкнутая система управления
будет устойчивой, если АФЧХ разомкнутой
системы при изменении частот от 0 до
∞ не охватывает точку (-1;j0)»
Построение:
1)
Записать передаточную ф-ию разомкнутого
контура (пр-ие всех передаточных ф-ий,
входящих в замкнутый контур) 2) Раскрыть
скобки и привести подобные 3) Сгруппировать
коэфф-ты числителя и знаменателя по
четным и нечетным степеням при Р. 4)
Заменить операторы Лапласа Р на jω.
5) Сгруппировать коэфф-ты с j
и без j,
т.е. разбить на действительную и мнимую
части. 6) Записать выражения P(ω)=…
и Q(ω)=…
7) Составить таблицу значений, построить
график. ЧХ
–
характеристика, отражающая изменение
фазы в зависимости от частоты в системе
или отдельном блоке. Построение:
выражение
фазы можно получить способом подставления
в передаточную ф-ию jω.
Получаем W(jω)=…
Получаем φ(ω)=arctg(aj+b)±…=arctg(a/b)±…
Составляем таблицу значений ω
и φ(ω).
По точкам строим график. Логарифмический
критерий устойчивости
– замкнутая система будет устойчивой,
если ЛАЧХ разомкнутого контура системы
пересекает ось частот в точке ωср
раньше, чем фазовая хар-ка разомкнутого
контура пересечет значение фазы -180˚.
ЧХ
–
характеристика, отражающая изменение
фазы в зависимости от частоты в системе
или отдельном блоке. Построение:
выражение
фазы можно получить способом подставления
в передаточную ф-ию jω.
Получаем W(jω)=…
Получаем φ(ω)=arctg(aj+b)±…=arctg(a/b)±…
Составляем таблицу значений ω
и φ(ω).
По точкам строим график. Логарифмический
критерий устойчивости
– замкнутая система будет устойчивой,
если ЛАЧХ разомкнутого контура системы
пересекает ось частот в точке ωср
раньше, чем фазовая хар-ка разомкнутого
контура пересечет значение фазы -180˚.
 2.
Коррекция САР.
Для чего: 1) Если система неустойчива,
то с помощью корректирующих у-в можно
привести САУ в устойчивое состояние
2) Обеспечение заданной динамической
точности системы (обеспечить необходимые
параметры переходного процесса: σ –
перерегулирование, tn
– время переходного процесса, М -
колебательность)
Построение:
1) строится ЛАЧХ разомкнутого контура
системы 2) рассматриваются параметры
среднечастотного участка
2.
Коррекция САР.
Для чего: 1) Если система неустойчива,
то с помощью корректирующих у-в можно
привести САУ в устойчивое состояние
2) Обеспечение заданной динамической
точности системы (обеспечить необходимые
параметры переходного процесса: σ –
перерегулирование, tn
– время переходного процесса, М -
колебательность)
Построение:
1) строится ЛАЧХ разомкнутого контура
системы 2) рассматриваются параметры
среднечастотного участка
 – зона нечувствительности
– зона нечувствительности искретные
системы управления
– если в системе используется хотя
бы один дискретный элемент. Дискретные
СУ описываются при помощи дискретного
оператора Лапласа z.
(W(z)=…)
Период квантования играет очень важную
роль. Если период квантования будет
очень маленький, то система будет
информационно перегружена. Если же
преиод квантования большой, система
окажется не точна. +высокая
помехозащищенность +хорошее
быстродействие +построение системы
на современной элементной базе
–существует погрешность преобразования
из аналогового сигнала в дискретный
и наоборот. Преобразование осуществляется
с помощью ЦАП и АЦП.
искретные
системы управления
– если в системе используется хотя
бы один дискретный элемент. Дискретные
СУ описываются при помощи дискретного
оператора Лапласа z.
(W(z)=…)
Период квантования играет очень важную
роль. Если период квантования будет
очень маленький, то система будет
информационно перегружена. Если же
преиод квантования большой, система
окажется не точна. +высокая
помехозащищенность +хорошее
быстродействие +построение системы
на современной элементной базе
–существует погрешность преобразования
из аналогового сигнала в дискретный
и наоборот. Преобразование осуществляется
с помощью ЦАП и АЦП. Двухконтурная
система управления ДПТ
Двухконтурная
система управления ДПТ анная
система упр-ия является двухконтурной
СУ подчиненного регулирования. Задание
для внутреннего контура вырабатывается
внешним контуром, т.е. внутренний
подчиняется внешнему. Каждый контур
имеет свое управляющее устройство и
ДОС. Внутренний контур тока якоря
является ведомым по внешнему контуру
скорости.
анная
система упр-ия является двухконтурной
СУ подчиненного регулирования. Задание
для внутреннего контура вырабатывается
внешним контуром, т.е. внутренний
подчиняется внешнему. Каждый контур
имеет свое управляющее устройство и
ДОС. Внутренний контур тока якоря
является ведомым по внешнему контуру
скорости. труктура
комплексного автоматического управления
предприятием.
труктура
комплексного автоматического управления
предприятием. ежимы
работы ДПТ с частотой вращения выше
номинальной обычно применяются при
работе двигателя без нагрузки (отвод
инструмента после завершения резания
для сокращения времени обработки
детали)
ежимы
работы ДПТ с частотой вращения выше
номинальной обычно применяются при
работе двигателя без нагрузки (отвод
инструмента после завершения резания
для сокращения времени обработки
детали)