
- •Министерство образования и науки Российской Федерации
- •Частотные характеристики типовых звеньев
- •1. Усилительное звено
- •2. Апериодическое звено первого порядка
- •3. Интегрирующее звено
- •4. Дифференцирующее звено
- •Порядок выполнения работы
- •Отчет по работе перед преподавателем
- •Список использованной литературы
- •Частотные характеристики динамических звеньев
- •410054, Г. Саратов, ул. Политехническая, 77
3. Интегрирующее звено
Передаточная
функция интегрирующего звена
![]() .
.
Частотные характеристики. Произведем замену в передаточной функции
![]()
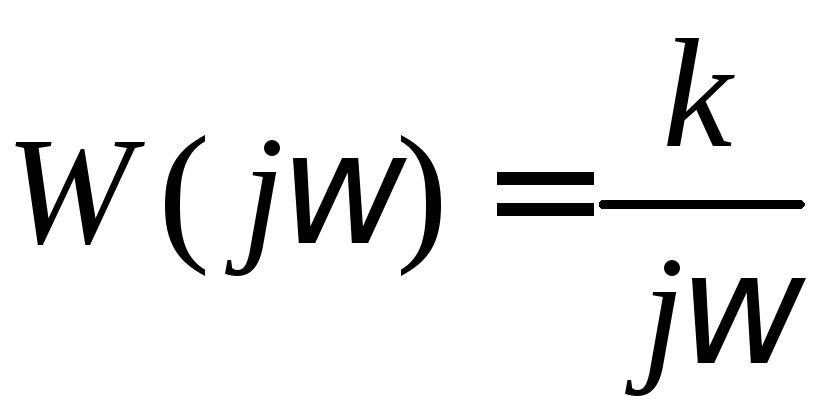 .
.
Амплитудная фазовая
частотная характеристика
![]() .
.
В ещественная
частотная характеристика
ещественная
частотная характеристика![]() .
.
Мнимая частотная характеристика
![]() .
.
Амплитудная частотная характеристика. Найдем модуль частотной характеристики (рис. 8).
![]() .
.
Фазовая частотная характеристика
![]() .
.
А мплитудная
фазовая частотная характеристика
мплитудная
фазовая частотная характеристика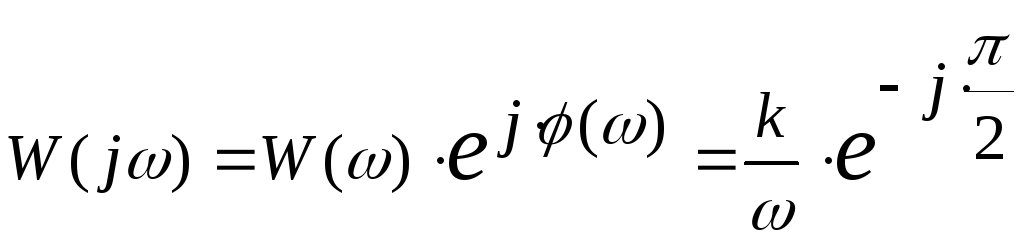
Таким образом,
модуль частотной характеристики
(коэффициент передачи) уменьшается с
увеличением частоты, а фазовый сдвиг
равен
![]() =const
(рис. 9).
=const
(рис. 9).
Логарифмические частотные характеристики.
![]() .
.
Рассмотрим численный пример
![]() ,
,
![]() ,
,
![]() .
.
Таким образом ЛАХ интегрирующего звена всегда имеет наклон -20дБ/дек. Для построения ЛАХ надо провести линию с наклоном через одну точку, принадлежащую ЛАХ (рис. 10).

Метод 1. Провести
линию через точку
![]() .
.
Метод 2. Выражение
для ЛАХ можно записать в виде
![]() .
.![]() когда
когда![]() .
.
Отсюда точка
![]()
![]() также принадлежит ЛАХ данного звена.
Для построения ЛАХ необходимо провести
линию с наклоном -20дБ/дек через эту
точку.
также принадлежит ЛАХ данного звена.
Для построения ЛАХ необходимо провести
линию с наклоном -20дБ/дек через эту
точку.
Метод 3. Провести линию через эти две найденные точки.
Интегрирующее
звено на всех частотах имеет отставание
по фазе
![]() (см. рис. 10).
(см. рис. 10).
4. Дифференцирующее звено
1. Дифференциальное
уравнение
![]() .
.
2 .
Частотные характеристики. Произведем
замену в передаточной функции
.
Частотные характеристики. Произведем
замену в передаточной функции![]()
![]() .
.
Амплитудная фазовая
частотная характеристика
![]() (см. рис. 11).
(см. рис. 11).
Вещественная
частотная характеристика
![]() .
.
Мнимая частотная
характеристика
![]() .
.
Амплитудная частотная характеристика.
Найдем модуль частотной характеристики.
![]() .
.
Фазовая частотная
характеристика
![]() .
.
Амплитудная фазовая частотная характеристика

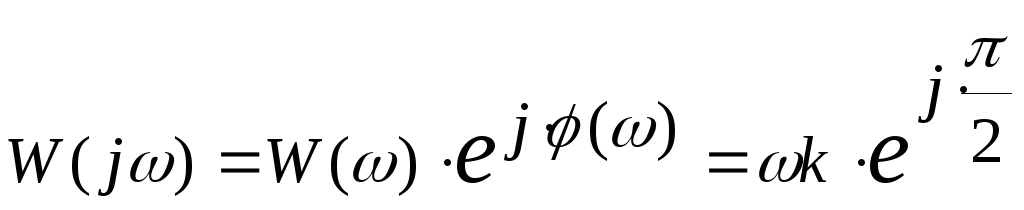 .
.
Таким образом,
модуль частотной характеристики
(коэффициент передачи) увеличивается
с увеличением частоты, а фазовый
сдвиг равен
![]() =const
(рис. 12).
=const
(рис. 12).
Логарифмические частотные характеристики.
![]() .
.
Рассмотрим численный пример
![]() ,
,
![]() ,
,
![]() .
.
Таким образом ЛАХ
интегрирующего звена всегда имеет
наклон +20дБ/дек. Для построения ЛАХ
надо провести линию с наклоном через
одну точку, принадлежащую ЛАХ, которой
может быть точка
![]() .
.
Дифференцирующее
звено на всех частотах имеет опережение
по фазе
![]() (рис. 13).
(рис. 13).

Порядок выполнения работы
Включить компьютер и вызвать MathCad.
Создать новый файл, дать файлу название и записать на жесткий диск. В дальнейшем в процессе работы периодически (один раз в 10-15 мин производить перезапись файла).
В первой строке ввести наименование лабораторной работы, фамилию, инициалы студента и номер группы (см. пример на с. 16-18).
Из таблицы, приведенной в приложении, ввести, согласно варианту, значения параметров элементов.
Ввести передаточную функцию звена первого порядка. Ввести мнимую единицу и частотный диапазон построения частотных характеристик. Заменить в передаточной функции
 .
Записать выражения для модуля и фазы
амплитудно-частотной характеристики
звена первого порядка. Построить
графики амплитудной и фазовой частотных
характеристик.
.
Записать выражения для модуля и фазы
амплитудно-частотной характеристики
звена первого порядка. Построить
графики амплитудной и фазовой частотных
характеристик.Ввести выражение для логарифмической частотной характеристики и построить графики амплитудной и фазовой логарифмических частотных характеристик. По шкале частот поставить логарифмический масштаб.
Ввести передаточную функцию звена второго порядка и аналогично построить частотные характеристики.
Изменить коэффициенты звена второго порядка, чтобы получить колебательное звено, если исходное апериодическое, или апериодическое, если исходное колебательное. Построить частотные характеристики для полученного звена.
Форматирование программы и графиков.
Установить границы страниц листа MathCad, используя команды меню Файл.
Перемещая элементы программы и графики, изменяя размеры графиков, добиться наглядного представления результатов и минимального количества страниц.
Используя команду «Предварительный просмотр» убедиться, что программа и графики находятся на нужных страницах.
Записать программу на дискету для использования при выполнении курсовой работы.
Распечатать работу на принтере.
