
- •Министерство образования и науки Российской Федерации
- •Частотные характеристики типовых звеньев
- •1. Усилительное звено
- •2. Апериодическое звено первого порядка
- •3. Интегрирующее звено
- •4. Дифференцирующее звено
- •Порядок выполнения работы
- •Отчет по работе перед преподавателем
- •Список использованной литературы
- •Частотные характеристики динамических звеньев
- •410054, Г. Саратов, ул. Политехническая, 77
Частотные характеристики типовых звеньев
1. Усилительное звено
К усилительным звеньям относятся элементы, производящие мгновенное преобразование входного сигнала в выходной без переходных процессов. К безынерционным звеньям относятся электронные усилители, механические жесткие рычажные системы и т.д.
Передаточная
функция безынерционного звена
![]()
Ч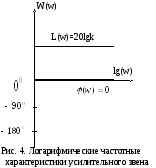 астотные
характеристики: АФЧХ, ВЧХ, МЧХ, АЧХ,
ФЧХ:
астотные
характеристики: АФЧХ, ВЧХ, МЧХ, АЧХ,
ФЧХ:
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]()
А мплитудно-фазовая
частотная характеристика приведена на
рис. 3.
мплитудно-фазовая
частотная характеристика приведена на
рис. 3.
Логарифмические
частотные характеристики (рис. 4)
определяются выражениями
![]()
![]() .
.
Амплитудная
характеристика для всех частот равна
![]() ,
сдвиг по фазе у данного звена отсутствует.
,
сдвиг по фазе у данного звена отсутствует.
2. Апериодическое звено первого порядка
Передаточная
функция
![]() .
.
Частотные
характеристики. Для получения частотной
характеристики сделаем замену в
передаточной функции
![]() ,
умножим полученное выражение на
сопряженный знаменателю сомножитель,
разделим полученную частотную
характеристику на реальную и мнимую
составляющие
,
умножим полученное выражение на
сопряженный знаменателю сомножитель,
разделим полученную частотную
характеристику на реальную и мнимую
составляющие
![]() .
.
Вещественная
частотная характеристика
![]() .
.
Мнимая частотная
характеристика
![]() .
.
Фазовая частотная
характеристика
![]() .
.
Амплитудная частотная характеристика
![]() .
.
Получим аналитическое выражение АФХ.
Проведем анализ
суммы
![]() .
.
Возведем левую и правую части в квадрат:
![]()
Или
![]()
![]() .
.
Тогда
![]() добавим
в обе части
добавим
в обе части![]() ,
получим
,
получим
![]() .
.
![]() - уравнение
окружности с центром в точке (0; k/2).
- уравнение
окружности с центром в точке (0; k/2).
Т аким
образом, АЧХ имеет вид полуокружности
(рис. 5). При=0
сдвиг по фазе равен нулю, коэффициент
передачи равен k.
С увеличением частоты модуль
уменьшается, а сдвиг по фазе стремится
от 0 к минус 90
аким
образом, АЧХ имеет вид полуокружности
(рис. 5). При=0
сдвиг по фазе равен нулю, коэффициент
передачи равен k.
С увеличением частоты модуль
уменьшается, а сдвиг по фазе стремится
от 0 к минус 90
(при , - 90).
Логарифмические частотные характеристики ЛЧХ.
![]() ;
;
![]() ;
;![]() .
.
Разобьем ЛАХ по оси частот на 2 диапазона.
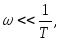
 - асимптота с
левой стороны.
- асимптота с
левой стороны.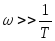 ,
,
 .
.
Рассмотрим это выражение на численном примере.
![]()
![]()
![]()
При увеличении
круговой частоты
![]() в
10 раз правое слагаемое увеличивается
на 20 единиц, т.е. после частоты среза
ЛАЧ имеет наклон 20 дБ/дек.
в
10 раз правое слагаемое увеличивается
на 20 единиц, т.е. после частоты среза
ЛАЧ имеет наклон 20 дБ/дек.
Эти данные позволяют достаточно просто строить ЛАЧ апериодического звена первого порядка (рис. 6).
1. Построить
вертикальную линию на частоте среза
![]() .
.
2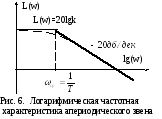 .
В диапазоне нижних частот от частоты
среза построить горизонтальную линию
.
В диапазоне нижних частот от частоты
среза построить горизонтальную линию![]() .
.
3. В диапазоне
высоких частот от частоты среза через
точку пересечения
![]() с вертикалью частоты среза провести
ниспадающую линию с наклоном 20 дБ/дек.
с вертикалью частоты среза провести
ниспадающую линию с наклоном 20 дБ/дек.
Эти две прямые линии дают амплитудную частотную характеристику звена в логарифмическом масштабе. Максимальное отклонение данной аппроксимации от расчетной кривой составляет 3дБ на частоте среза.
Логарифмическая
фазовая характеристика ЛФХ строится
по шаблону или расчетным путем по
выражению
![]() .
.
На низких частотах
выходной сигнал совпадает по фазе с
входным
![]() ,
затем появляется отставание по фазе,
которое на частоте среза равно
,
затем появляется отставание по фазе,
которое на частоте среза равно
![]() .
Максимальное отставание по фазе
составляет
.
Максимальное отставание по фазе
составляет![]() .
.
Пример построения
логарифмических частотных характеристик
для звена первого порядка
![]() приведен на рис. 7.
приведен на рис. 7.

