3. Операторный метод решение дифференциального уравнения

на основе передаточной функции

Для решения дифференциальных уравнений широко применяется операторный метод. Запишем полученной дифференциальное уравнение механической системы

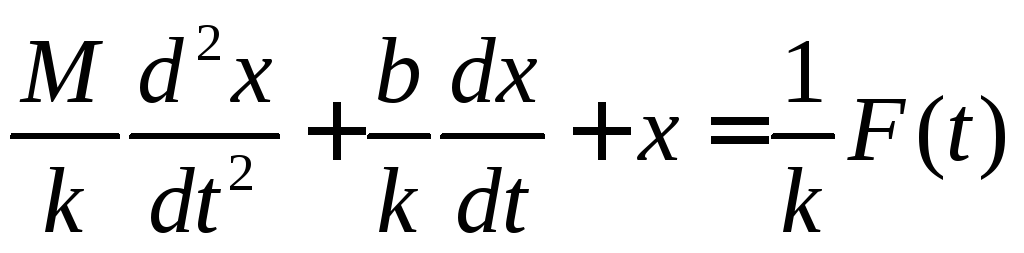
Данное уравнение содержит три величины:

1. Функцию изменения во времени входного сигнала .

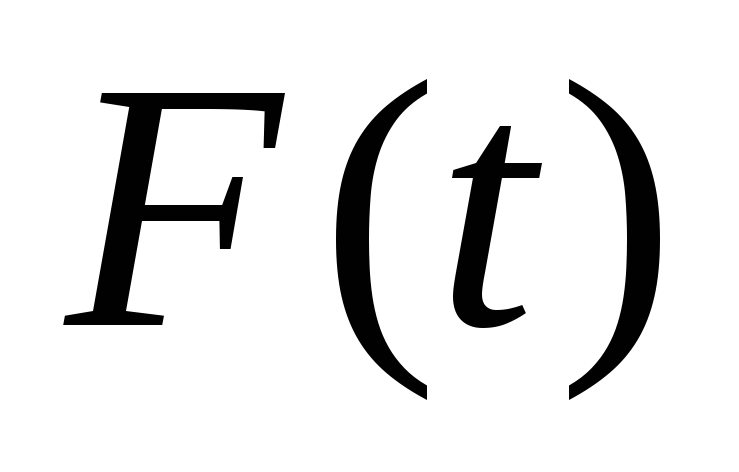2. Функцию изменения во времени выходного сигнала .

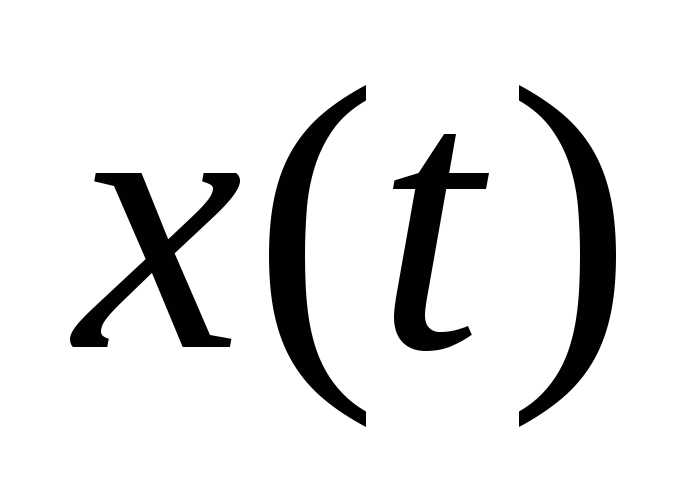3. Само дифференциальное уравнение, являющееся оператором преобразования входной функции времени 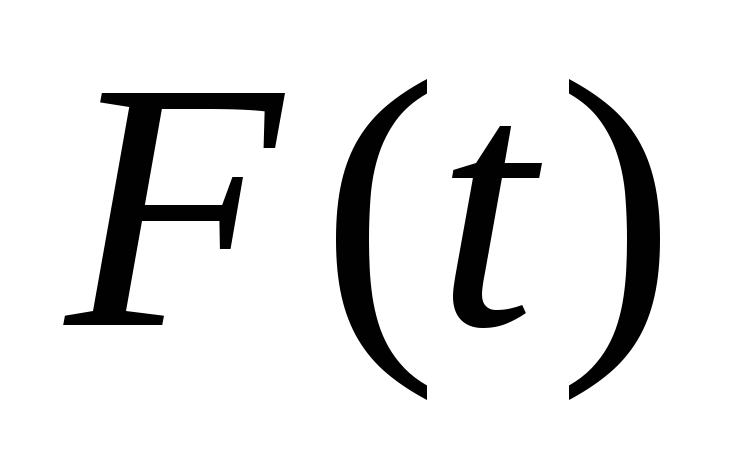в выходную функцию времени.

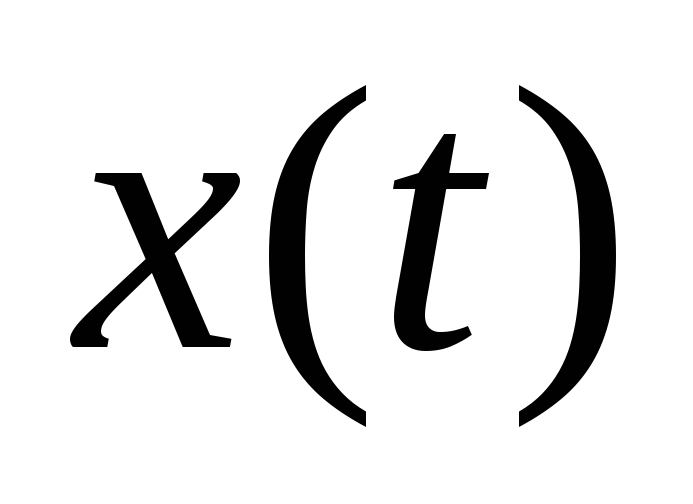В основе операторного метода решения дифференциальных уравнений лежит преобразование Лапласа. При этом производится преобразование временных функции и дифференциального уравнения в функции и оператор комплексной переменной().

Прямое преобразование Лапласа .

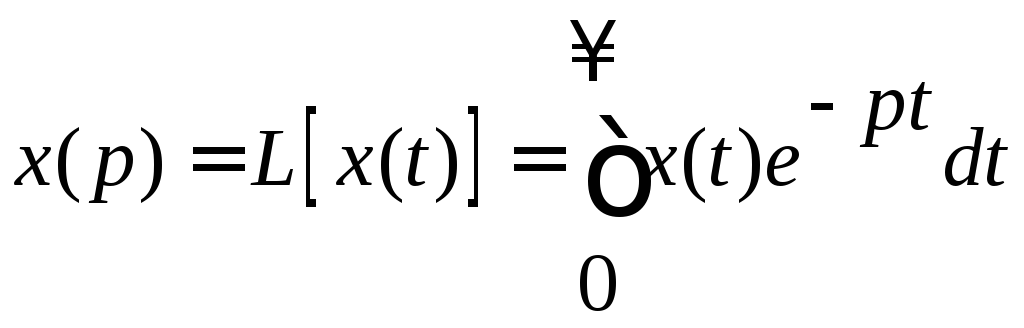называется изображением по Лапласу временной функции

Обратное преобразование Лапласа имеет вид .

Алгоритм решения задачи символическим методом заключается в следующем (рис. 4):

1. Записывается дифференциальное уравнение, описывающее закономерности рабаты динамического звена

2. Делается преобразование дифференциального уравнения по Лапласу в оператор комплексной переменной

1) вместо записываются функции комплексной переменной

,

2) В дифференциальном уравнении производные первого, второго и т.д. порядков заменяются на оператор и т.д., а именно,

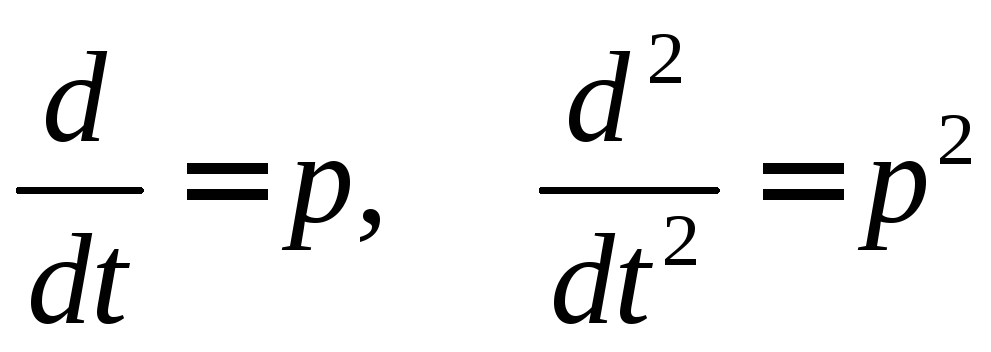и т.д.,

например

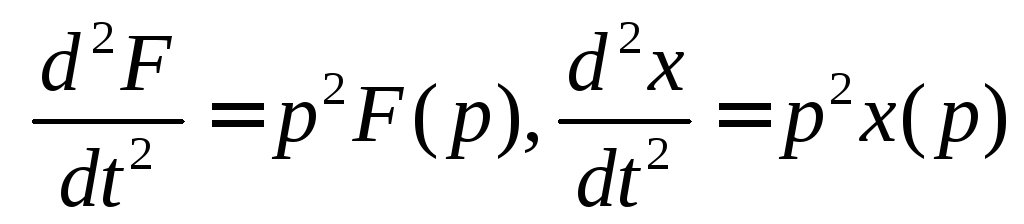
В данном случае преобразованное по Лапласу уравнение имеет вид

.

Оно является алгебраическим. Умножение в комплексной плоскости на оператор означает, что во временной плоскости производится дифференцирование. Деление в комплексной плоскости на операторозначает обратное действие - интегрирование.

3. Находится преобразование Лапласа от закона изменения входной переменной.

Для этого существуют таблицы преобразования Лапласа в справочниках, а также команды символьных преобразований в математических процессорах компьютеров.

4. Полученное алгебраическое уравнения решается относительно выходной переменной

5. Находится обратное преобразование Лапласа от

,

которое является искомым решением и описывает изменение во времени выходной переменной.

Преобразование Лапласа дифференциального уравнения приводит к удобному и широко применяемому выражению связи между изображениями входной и выходной величин черезпередаточную функцию.

Рассмотрим выражение, полученное после применения преобразования Лапласа к дифференциальному уравнению,

В левой части является множителем и его можно вынести за скобки

Найдем отношение

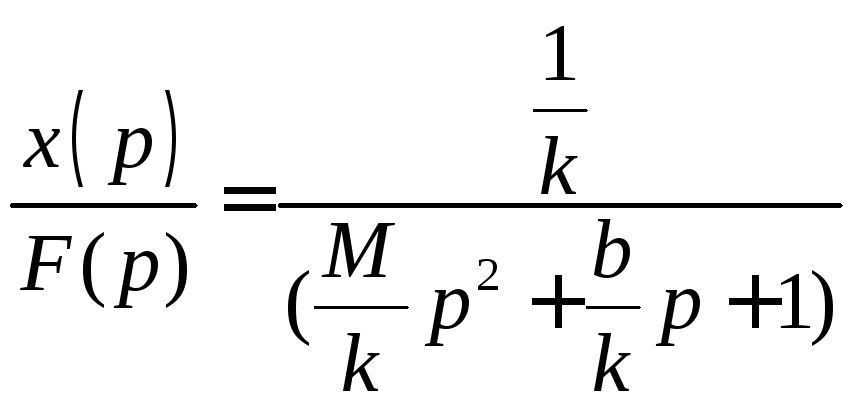
Отношение изображения выходной величины системы к изображению входной величины называется передаточной функциейи обычно обозначается. В данном случае передаточная функция равна

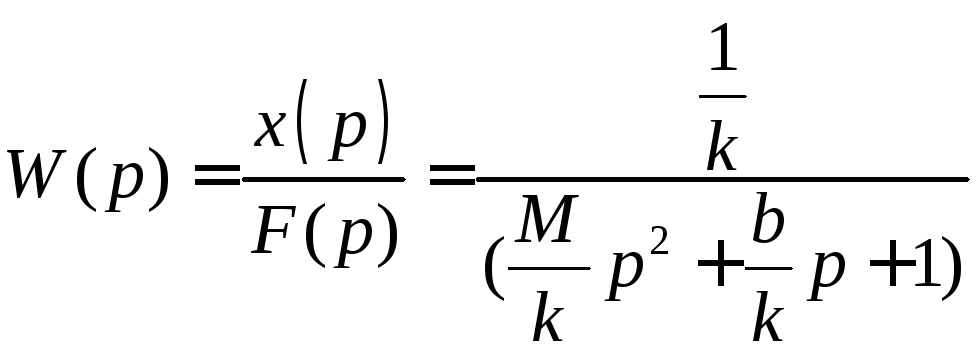
При известной передаточной функции изображение выходной пере менной находится как произведение передаточной функции на изображение входной переменной .

что существенно упрощает анализ элементов и систем управления.

В системеMatLabпри использовании передаточной функции входная переменнаи выходная переменнаавтоматически преобразуются по Лапласу без участия исследователя. Схема моделирования рассмотренной системы на основе передаточной функции имеет вид, представленный на рис. 5. Следует отметить условность схемы, т.к. передаточная функция относится к преобразованиям Лапласа входной и выходной величин. Кроме того, следует отметить, что передаточная функция описывает зависимость выходной переменной от входной только при нулевых начальных условиях.