
Международный Университет
Бизнеса и Управления
БАЛАКОВСКИЙ
ИНСТИТУТ
БИЗНЕСА И УПРАВЛЕНИЯ
ПРАКТИЧЕСКАЯ РАБОТА
«АНАЛИЗ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ПО ИНТЕГРАЛЬНОМУ КРИТЕРИЮ КАЧЕСТВА»
Методическое пособие к практическим работам по курсу: «Теория автоматического управления»
для студентов специальностей 210100 – «Управление и информатика в технических системах»
230700 – «Сервис», 351400 – «Прикладная информатика»,
Одобрено
Редакционно-издательским
советом
Балаковского Института
Бизнеса и Управления
Балаково 2004
ЦЕЛЬ РАБОТЫ:научиться вычислять квадратичную интегральную оценку качества процесса регулирования
Теоритические положения
В основе анализа качества САУ по интегральному квадратичному критерию качества (ИКК) лежит интегральный показатель, характеризующий отклонение регулируемого параметра при переходном процессе от идеализированного переходного процесса. В качестве идеального переходного процесса обычно принято считать ступенчатый переходный процесс, протекающий мгновенно, без перерегулирования. (Рисунок 5.1 а)
Вычисление ИКК производится по формуле:
![]() (5.1)
(5.1)
где х(t) - уравнение переходной функции;
х(![]() )
- установившееся значение регулируемого
параметра.
)
- установившееся значение регулируемого
параметра.
Как видно но формуле (5.1) ИКК не зависит от знака ошибки регулирования, т.к. эта величина берется в квадрате. Она еще называется "квадратичной площадью ошибки регулирования".
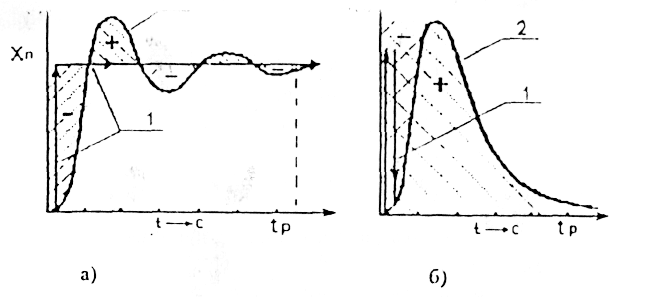
Рисунок 5.1 - Графики переходного процесса
а)при входном сигнале в виде единичного ступенчатого воздействия,
б)при входном сигнале в виде единичного импульса.
1 идеализированный переходный процесс,
2 реальный переходный процесс.
Заштрихованная область показывает отклонение реальною переходного процесса от идеального;
знак (-) характеризует отставания реального переходного процесса от идеального;
знак (+) характеризует опережение реального переходного процесса по сравнению с идеальным.
Вычисление ИКК при ступенчатом входном сигнале
Пусть на вход САУ подан единичный, ступенчатый сигнал, тогда изображение по Лапласу выходной координаты имеют вид:
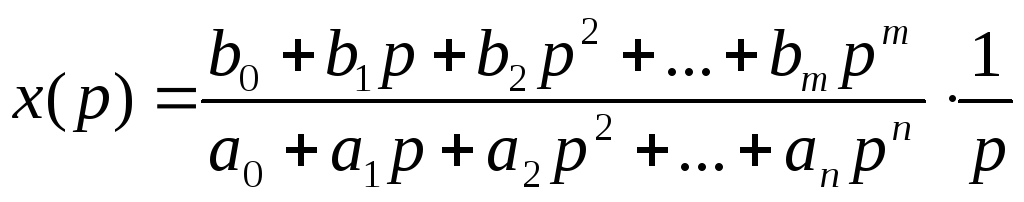 (5.2)
(5.2)
Интеграл
![]() можно вычислить, не производя обратного
преобразования Лапласа, не решая
дифференциального уравнения, не вычисляя
затем интеграл (5.1), а сразу по коэффициентам
формулы (5.2) [ 5, 7 ]
можно вычислить, не производя обратного
преобразования Лапласа, не решая
дифференциального уравнения, не вычисляя
затем интеграл (5.1), а сразу по коэффициентам
формулы (5.2) [ 5, 7 ]
![]() (5.3)
(5.3)
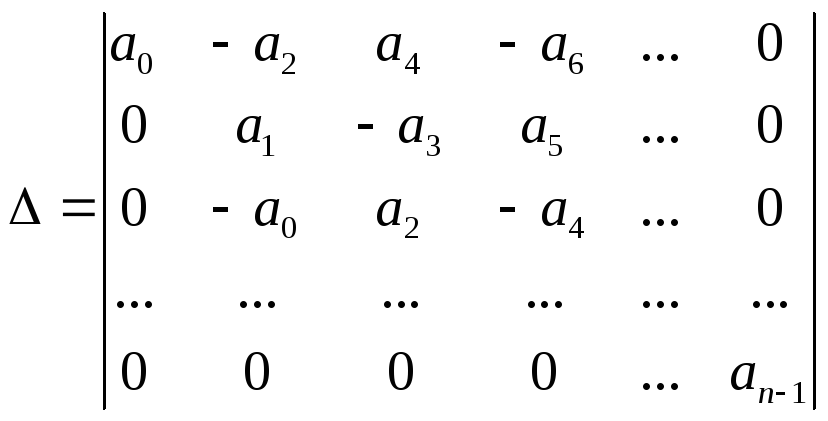
![]() определитель
получаемый из
определитель
получаемый из![]() путем заменыi+1
столбца столбцом вида
путем заменыi+1
столбца столбцом вида
![]()
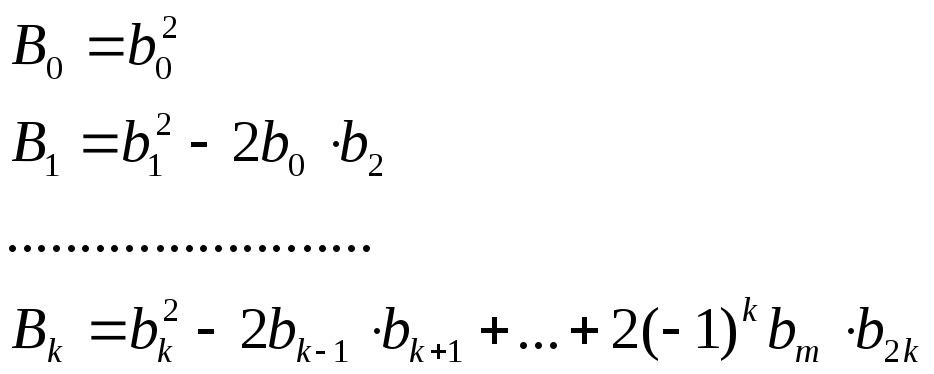
Таким
образом, определение
![]() проводится через раскрытие определителя
Гурвица (д) и преобразованных определителей
(
проводится через раскрытие определителя
Гурвица (д) и преобразованных определителей
(![]() ,
,![]() ,...),
что является трудоемким процессом.
Поэтому для САУ пятого и выше порядка
он практически не применяется. Пусть
для системы 4-го порядка изображение по
Лапласу регулируемого параметра при
скачкообразном входном воздействии
имеет вид:
,...),
что является трудоемким процессом.
Поэтому для САУ пятого и выше порядка
он практически не применяется. Пусть
для системы 4-го порядка изображение по
Лапласу регулируемого параметра при
скачкообразном входном воздействии
имеет вид:
![]() (5.4)
(5.4)
Определяем
значение
![]() по формуле (5.3)
по формуле (5.3)
 (5.5)
(5.5)
После раскрытия определителей формула (5.5) для системы 4-го порядка принимает вид:
 (5.6)
(5.6)
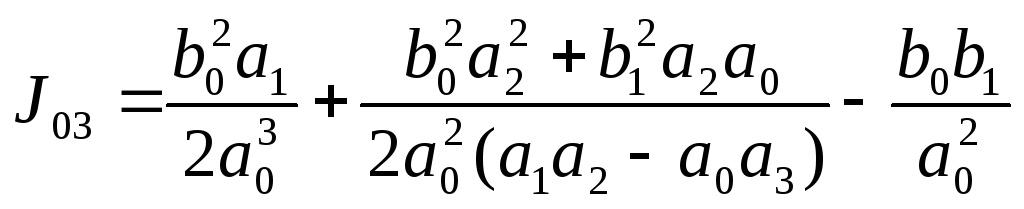 (5.7)
(5.7)
Для системы 2-го порядка
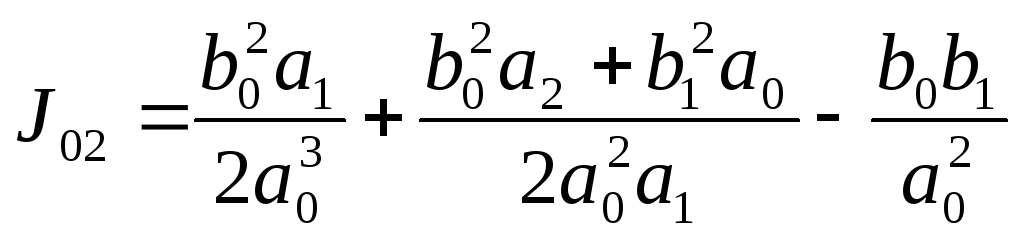 (5.8)
(5.8)
Для системы 1-го порядка
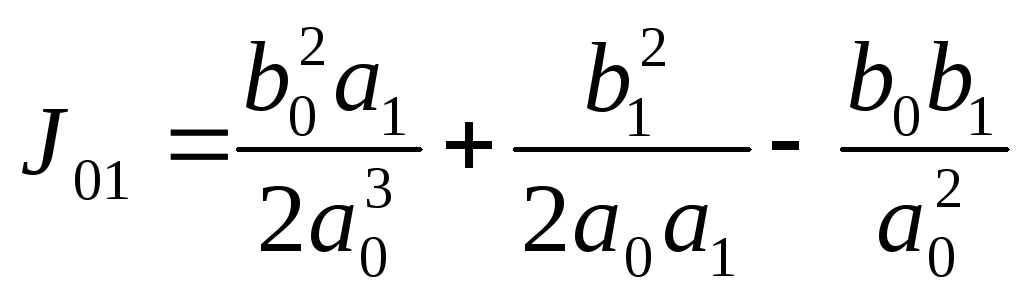 (5.9)
(5.9)
ПРИМЕР 1 Передаточная функция системы имеет вид:
![]()
Определить оптимальное значение постоянной времени Т, соответствующую минимуму ИКК пли максимальному быстродействию системы при подаче на и ход системы ступенчатого сигнала И(t) = I(t) при следующих параметрах К=10с-1, Т, = 0.06с-1, Т, = 0.04с1.
РЕШЕНИЕ
1
Изображение по Лапласу выходной величины
имеет вид: ![]()
2
В соответствии с формулой (5.7) и с учетом
![]() находим
значение ИКК
находим
значение ИКК
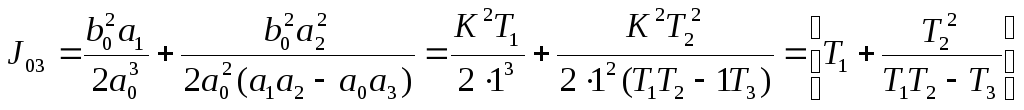
3 Для определения оптимального значения постоянной времени Т1 соответствующего минимум ИКК, определим производную ИКК по Т, и приравняем ее нулю
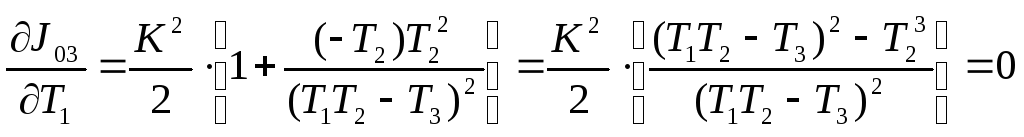
Из этого определяем значение Т1
![]()
![]()
Примечание
– проверим правильность полученного
уравнения. Для этого определим значение
![]() при разных значениях Т1.
при разных значениях Т1.
|
При
|
|
|
При
|
|
|
При
|
|
ОТВЕТ:
Оптимальное значение Т1
по
критерию минимум ИКК равно
![]()
Вычисления ИКК при импульсном входном сигнале
Пусть на вход системы подано возмущение в виде единичного импульса. Переходный процесс в виде импульсной переходной характеристики (весовая функция) показан па рисунке 5.16. Идеальный переходный процесс - это импульс с коэффициентом передачи К. Различие между идеальным и реальным переходным процессом показано в виде заштрихованной области и ее величина может быть оценена через ИКК [5,7]. Изображение по Лапласу функции веса имеет вид
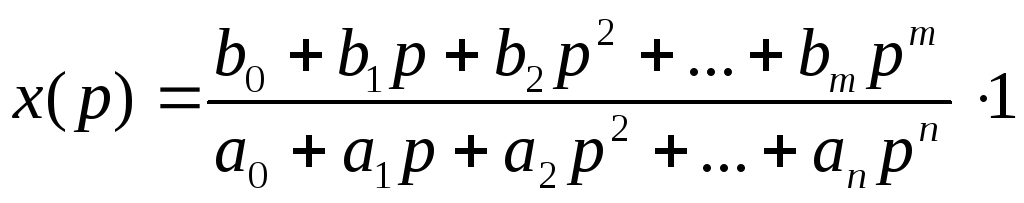 (5.10)
(5.10)
ИКК весовой функции определяется по другой формуле [5,7]
![]() (5.11)
(5.11)
Значение
![]() ,
,![]() ,...
,...![]() и В1
определяется также, как в формуле (5.3).
Пусть изображение по Лапласу весовой
функции имеет вид:
и В1
определяется также, как в формуле (5.3).
Пусть изображение по Лапласу весовой
функции имеет вид:
![]()
Определяем
значение
![]() по формуле (5.11)
по формуле (5.11)
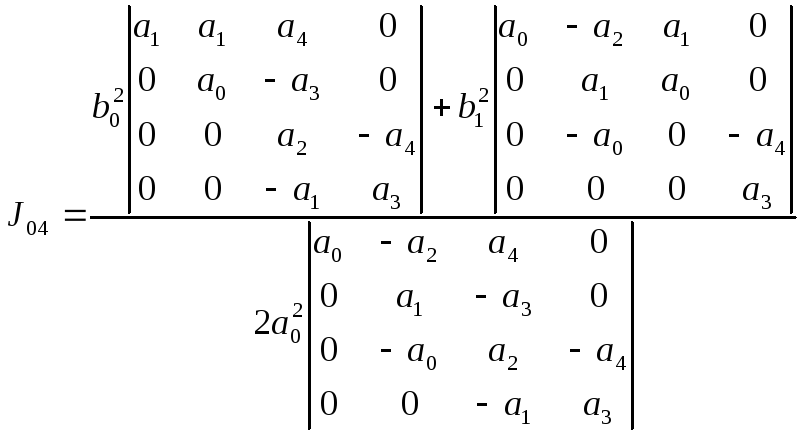 (5.12)
(5.12)
После раскрытия определителей формула (5.12) для системы 4-го порядка принимает вид:
 (5.13)
(5.13)
![]() (5.14)
(5.14)
Для системы 2-го порядка
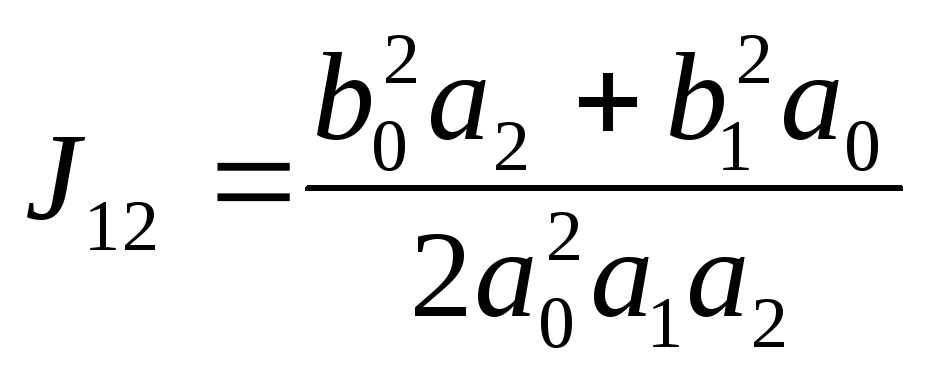 (5.15)
(5.15)
Для системы 1-го порядка
![]() (5.16)
(5.16)
ПРИМЕР 2 Передаточная функция системы имеет вид:
![]()
Определить оптимальное значение К1 по критерию минимум ИКК при подаче на вход U(t)=I(t). Параметры системы К1=20с1, Т = 0.1с2
РЕШЕНИЕ
1 Передаточная функция замкнутой системы
![]()
2 Изображение по Лапласу выходной величины
![]()
В соответствии с формулой (5.15) находим ИКК:
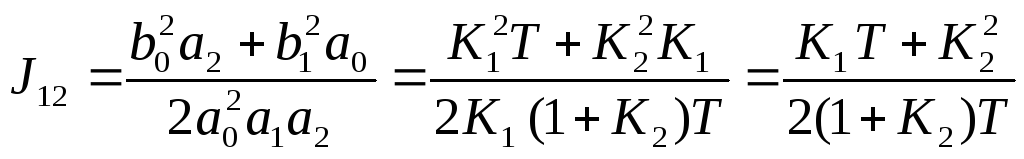
Для определения оптимального значения К2 соответствующего минимум ИКК, определим производную ИКК по К2 и приравняем ее нулю
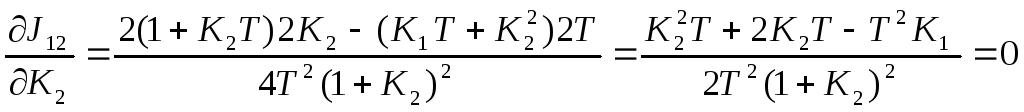
5 Из этого значения определяем значение К2 при К1=20с1, Т = 0.1с2
![]()
![]()
Примечание
- проверим правильность полученного
уравнения. Для этого определим значение
![]() при разных значениях К2.
при разных значениях К2.
|
При
|
|
|
При
|
|
|
При
|
|
ОТВЕТ:
Оптимальное значение К2
по
критерию минимум ИКК равно
![]()
Анализ САУ по улучшенному интегральному критерию качества
Недостаток ИКК в том, что при приближении действительной переходном функции к идеальной увеличивается колебательность и перерегулирование, уменьшается запас устойчивости.
Поэтому широко применяется другая интегральная оценка, которая называется улучшенным интегральным квадратичным критерием (УИКК). Он вычисляется по формуле:
![]() (5.17)
(5.17)
УИКК так же характеризует "квадратичную площадь ошибки регулирования", по не относительно ступенчатом переходной функции, а определяется относительно экспоненциальной переходной функции с постоянной времени т (рисунок 5.2) и вычисляется УИКК по тем же формулам, как и ИКК.[5,7]

Рисунок 5.2 - Графики переходной функции
1 идеальная переходная функция с ограничением по скорости возрастания
2 реальная переходная функция;
заштрихованная область - отклонение реального переходного процесса от идеального.
![]()
Определить оптимальное значение К по критерию минимума УИКК мри подаче на вход U(t)=I(t). Параметры системы T = 0,5с, ограничение по скорости выходного сигнала равно т = 0,2с. РЕШЕНИЕ
1 Передаточная функция замкнутой системы:
![]()
Изображение по Лапласу выходной величины с учетом ограничения скорости т2
![]()
3 Как видно из полученного изображения регулируемой величины значения УИКК можно представить как сумму двух ИКК. Первый ИКК определяется по формуле (5.8) при b1= 0.
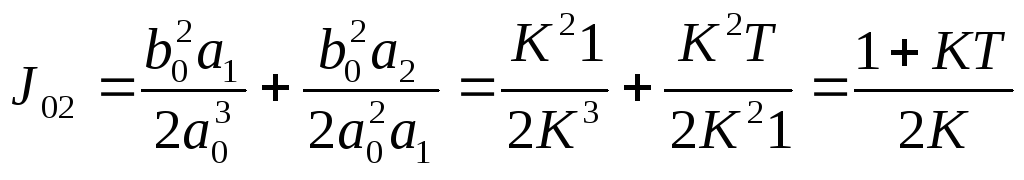
Второй ИКК определяется по формуле (5,15) при b1= 0:
![]()
Результирующее значение УИКК:
![]()
Для нахождения оптимального значения К определим производную УИКК по К и приравняем ее к 0.
![]()
из этого уравнения определяем значение К: по УИКК К=5с-1
Вычисление ИКК по ПФ ошибки регулирования
В некоторых случаях нахождение оптимального параметра по критерии минимума ИКК или минимума УИКК по изображению выходкой координаты по формуле (5.2) или (5.10) бывает достаточно сложным. Тогда ИКК или УИКК вычисляется по переходной составляющей ошибки регулирования.
Если дана передаточная функция замкнутой САУ, то изображение переходной составляющем ошибки регулирования определяется, но формуле:
![]() (5.18)
(5.18)
Если дана передаточная функция разомкнутой САУ, то изображение переходной составляющей ошибки регулирования определяется но формуле:
![]() (5.19)
(5.19)
Покажем определение ИКК по а(р) из конкретных примерах. [ 7 ]
ПРИМЕР 4 Передаточная функция замкнутой САУ имеет Вид
![]()
Определить
оптимальное значение коэффициента
затухания
![]() по критерию минимума ИКК при входном
сигналаU(t)
=I
(t).
по критерию минимума ИКК при входном
сигналаU(t)
=I
(t).
РЕШЕНИЕ I Определяем ИKK но изображению регулируемой величины х(р)
1 Изображение регулируемой величины при входном сигнале U(t) =I (t).
![]()
2 В соответствии с формулой (5.8) находим ИКК
![]()
3
Определим производную ИКК по
![]() и
приравниваем ее к 0
и
приравниваем ее к 0
![]()
Из
этого определяем значение
![]()
![]() =0
=0
![]()
ОТВЕТ:
Оптимальное значение
![]() =0,5
=0,5
РЕШЕНИЕ 2 Определяем ИКК по переходной составляющей ошибки регулирования а(р)
1
Как видно из решения 1 значение коэффициента
усиления К на нахождение оптимального
значение
![]() влияния не оказывает. Поэтому для
упрощения расчета принимаем К = 1.
влияния не оказывает. Поэтому для
упрощения расчета принимаем К = 1.
![]()
3 В соответствии с формулой (5.15) находим ИКК:
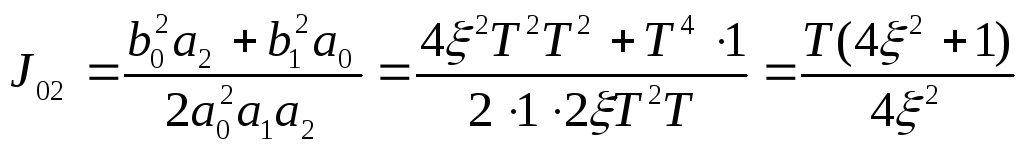
4
Определяем производную ИКК по
![]() и приравнивая ее к 0
и приравнивая ее к 0
![]()
Из
этого уравнения определяем
![]()
![]() =0
=0
![]()
ОТВЕТ:
Оптимальное значение![]() по ИКК, полученное двумя способами,
полностью совпадает и равно
по ИКК, полученное двумя способами,
полностью совпадает и равно![]() =0,5
=0,5
ПРИМЕР 5 Передаточная функция разомкнутой системы имеет вид
![]()
Определить оптимальное значение Т1 по критерию минимума ИКК при подачи на вход U(t) =I (t). Определение оптимального значение Т1, провести двумя способами.
РЕШЕНИЕ а) по изображению регулируемой величины х(р)
Передаточная функция замкнутой системы:
![]()
2 Изображение регулируемой величины
![]()
3 Значение ИКК по формуле (5.8)
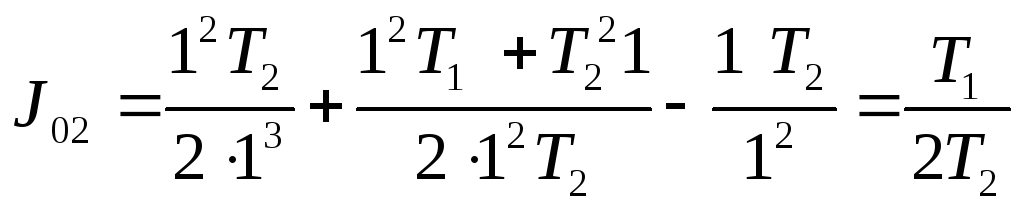
4
Очевидно что
![]() при
при![]()
РЕШЕНИЕ: 6) по изображению составляющей ошибки регулирования а(р)
I Изображение переходной составляющей ошибки регулирования по формуле (5.18)

2 Значение ИКК по формуле (5.15)
![]()
3
Очевидно что
![]() при
при![]()
ОТВЕТ: Оптимальное знамение Т1 полученное через х(р) и а(р) , полностью совпадает и равно Т1 —> 0.
ВЫВОД: Если через изображения выходной величины х(р) не удается получить оптимального значения исходного параметра, то это можно сделать через изображение переходной составляющей ошибки регулирования а(р), потому что так называемая "квадратичная площадь ошибки регулирования" в обеих случаях совершенно одинакова.
