Центральный институт непрерывного образования (Общество «Знание» России) БАЛАКОВСКИЙ ИНСТИТУТ БИЗНЕСА И УПРАВЛЕНИЯ

Анализ НЕЛИНЕЙНОЙ сАУ со старшей производной в ЗАКОНЕ управлениЯ

Методические указания для студентов

специальностей:

210100 (код 65) - Управление и информатика в технических системах;

080507 (код 65) – Менеджмент организации;

080801 (код 65) – Прикладная информатика (в автомобилях и автомобильном хозяйстве).

Одобрено Редакционно-издательским советом Балаковского Института Бизнеса и Управления

Балаково 2007

Цель работы: Исследовать свойства замкнутой системы с различными дифференцирующими фильтрами, оценить влияние возмущения и помехи измерения на характер переходных процессов.

Основные сведения

Свойство системы можно интерпретировать графически в пространстве состояний, т.е. в пространстве размерности n, координатами которого являются переменные состояния исследуемого объекта или системы.

Рисунок 1 – Пространство состояний

Состояние объекта или системы в произвольный момент времени изображается точкой пространства состояний, которая называется изображающей точкой объекта.

В работе исследуется объект управления, описываемый уравнением:

(1)

где - возмущение;

;

.

На основании требований к качеству переходных процессов в замкнутой системе ( и ) формируется желаемое дифференциальное уравнение того же порядка, что и уравнение объекта.

(2)

так, чтобы в статике выполнялось условие , где - входное воздействие на систему. Согласно методу синтеза управляющее воздействие имеет вид:

, (3)

где - коэффициент усиления регулятора, численное значение которого приближенно можно определить по соотношению .

На практике для организации управления (3) с целью оценки производных и используют дифференцирующий фильтр, который в простейшем случае описывается уравнением:

, (4)

где и являются оценками и ;

- коэффициент демпфирования, обеспечивающий переходные процессы в фильтре близкие к монотонным;

- постоянная времени фильтра, которая выбирается из условия ;

- желаемая постоянная времени.

Рассчитанный таким образом фильтр будем называть «быстрым». На рисунке 2 показана схема системы с дифференцирующим фильтром второго порядка.

Исследование свойств системы осуществляется с помощью метода разделения движений, причем быстрой составляющей соответствует контур, приведенный на рисунке 3.

Характеристическое уравнение контура быстрых движений (КБД) имеет вид:

и может быть представлено в стандартной форме

, (5)

где - постоянная времени контура; (6)

- коэффициент демпфирования.

Если рассчитывать параметры контура быстрых движений из условия разделения движений и монотонности переходного процесса в нем , то найденные по соотношениям (6) параметры дифференцирующего фильтра и соответствуют фильтру, который будем называть «медленным».

Наличие в системе помехи измерения приводит к необходимости повышать хотя бы на единицу порядок дифференцирующего фильтра, передаточная функция которого имеет вид:

, (7)

где параметры А и В выбираются из условия устойчивости контура быстрых движений, а постоянная времени рассчитывается для «быстрого» или «медленного» фильтра.

Методические указания

1. В работе в качестве объекта управления используется звено второго порядка, описываемое дифференциальным уравнением:

,

численные значения коэффициентов которого приведены в таблице 1.

2. Приступая к работе, необходимо (в соответствии с номером варианта) сформировать желаемое дифференциальное уравнение и определить параметры «быстрого» и «медленного» дифференцирующего фильтров 2-го порядка.

3. При исследовании свойств системы с помощью программных продуктов, следует в качестве метода интегрирования использовать метод Рунге-Кутта 4-го порядка точности и уменьшить в два раза шаг интегрирования.

4. При исследовании быстрой переменной необходимо вводить масштаб не более 0,05.

5. Пункты задания, отмеченные символом *, выполняются по указанию преподавателя.

6. При исследовании работы системы с «медленным» фильтром следует подключить вход усилителя (с коэффициентом с1) непосредственно к выходу объекта.

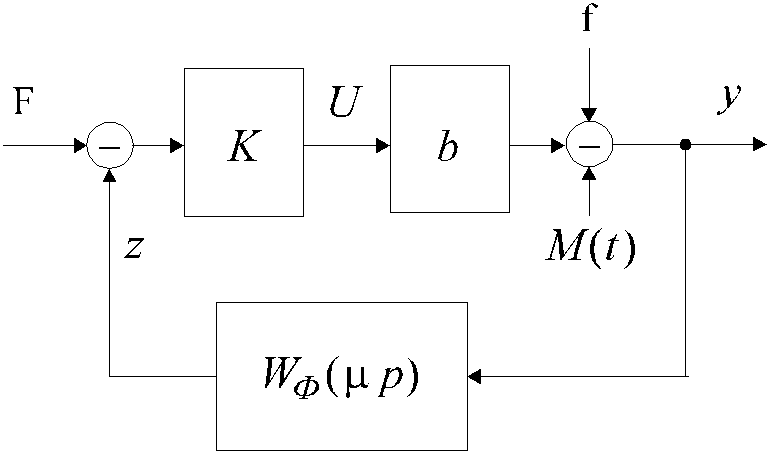
Рисунок 1 Схема контура быстрых движений

Рисунок 2 - Структурная схема замкнутой системы

Порядок выполнения работы

1. Определить параметры регулятора и фильтра на основании требований к качеству работы системы (таблица 1) для объекта вида (1).

Оценить качество переходных процессов объекта по переменной при , при нулевых начальных условиях.

Таблица 1.

Параметр	1	2	3	4	5	6	7	8
	2	3	1	3	2	1	4	2
	1	2	1	4	3	2	1	5
	0.6	1	2	1	0.5	2	0.6	0.7
	3	1	4	2	3	1	2	1
	30	10	0	0	30	15	20	10

2. Набрать модель замкнутой системы с «быстрым» фильтром 2-го порядка и зарисовать переходной процесс для медленной и быстрой переменной при , при нулевых начальных условиях. Проверить, соответствует ли качество переходного процесса желаемому.

3. Сравнить измеренные значения и с действительными и при нулевых начальных условиях.

4. Исследовать влияние на процессы и , изменяя в диапазоне (1-100) при нулевых начальных условиях.

5. Подавая на объект возмущение , зарисовать процессы и для рассчитанного значения ; здесь , - момент возникновения возмущения.

6. Оценить влияние помехи на и . При этом на вход фильтра следует подавать , где в качестве помехи использовать гармонический сигнал с амплитудой и несколькими значениями периода из диапазона .

7. Исследовать влияние параметров фильтра на характер процессов, задавая и , рассчитанные из условия «медленного» дифференцирующего фильтра. Сравнить результаты с процессами, полученными в п. 2. Зарисовать переходной процесс . Проверить, соответствует ли качество переходного процесса желаемому.

8. Вместо включить в систему нелинейный элемент типа «ограничение» и исследовать влияние величины ресурса управления на характер процессов в системе. Зарисовать и при и нескольких значениях , выбранных из диапазона (5-20).

Содержание отчета

1 Цель работы.

2 Результаты расчета параметров регулятора и дифференцирующих фильтров.

3 Структурные схемы систем с дифференцирующими фильтрами.

4 Графики всех переходных процессов.

5 Выводы по работе.

Контрольные вопросы

1 Как формируется закон управления в системах с вектором скорости?

2 Какова роль контура быстрых движений в системах с вектором скорости?

3 С какой целью в систему вводят дифференцирующий фильтр?

4 Как рассчитать параметры дифференцирующего фильтра в системах без помех и при наличии помех?

5 Как оценить влияние малой инерционности фильтра на свойства замкнутой системы?

СПИСОК ЛИТЕРАТУРЫ

1. Топчеев Ю.И. Атлас для проектирования систем автоматизиро­ванного регулирования. М: Машиностроение. 1989.

2. Иващенко Н.Н. Автоматическое регулирование. М.: Машгиз. 1962.

3. Справочное пособие по теории автоматического управления. Под ред. Е.А.Санковского. МН.: Высшая шк. 1973.-584 с.

4. Гузенко А.И. Основы теории автоматического регулирования. Под ред. В.В. Солодовникова. М.:высшая шк. 1977. – 408 с.

Анализ НЕЛИНЕЙНОЙ сАУ со старшей производной в ЗАКОНЕ управлениЯ

 Балаковский Институт Бизнеса и Управления

Методические указания для студентов

специальностей:

210100 (код 65) - Управление и информатика в технических системах;

080507 (код 65) – Менеджмент организации;

080801 (код 65) – Прикладная информатика (в автомобилях и

автомобильном хозяйстве).

Составитель:

СКОРОБОГАТОВА Татьяна Николаевна

Рецензент: Власов Вячеслав Викторович

Редактор: Пономарева Марина Вячеславовна

Лицензия Код 221 Серия ИД № 03989 от 12.02.01 г.

Подписано в печать 09.04.07 г. Формат 60х84 1/16

Бум. Тип. Уч.-изд. л 0,75

Тираж 100 экз. Заказ 02-04/07

_______________________________________________

Подготовка оригинал-макета–

Балаковский Институт Бизнеса и Управления

Печать тиража – Ризограф «Print-Fix»

Балаковский Институт Бизнеса и Управления

413800, г. Балаково Саратовской области,

ул. Транспортная, 4