
РГР / ТАУ практика / 2 Перед. фун. брошюра
.docМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОСИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНГИЮ
ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ
ЮЖНОГО ФЕДЕРАЛЬНОГО УНИВЕРСИТЕТА В
г. ТАГАНРОГЕ
Факультет автоматики и вычислительной техники
Кафедра систем автоматического управления__
© Тесленко О.А.
Практическое занятие 2
Дисциплина «Основы автоматического управления»
Тема: Вывод передаточной функции, динамических, статических и частотных характеристик динамического звена
Таганрог 2010
Вывод передаточной функции корректирующей цепи
Изучить материалы Л1 и Л2.
1. Пример. Вывод
передаточной функции
![]() -цепи
первого порядка
-цепи
первого порядка
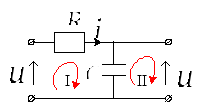
Дано. принципиальная схема корректирующей цепи
1000
0,5
![]()
![]()
Требуется вывести
передаточную функцию
![]() ,
исследовать статические, динамические
и частотные свойства корректирующей
цепи.
,
исследовать статические, динамические
и частотные свойства корректирующей
цепи.
Решение
-
На основе II-го правила Кирхгофа составим систему уравнений
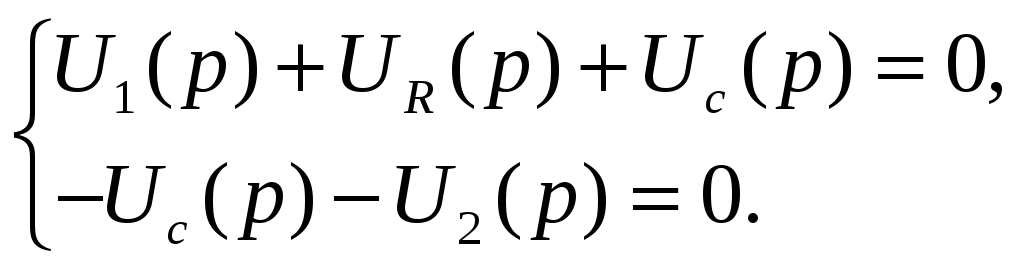 (1)
(1)
С учетом того, что
падения напряжений на элементах цепи
равны соответственно
![]() ,
,
![]() ,
перепишем полученную систему уравнений
(1) в виде
,
перепишем полученную систему уравнений
(1) в виде
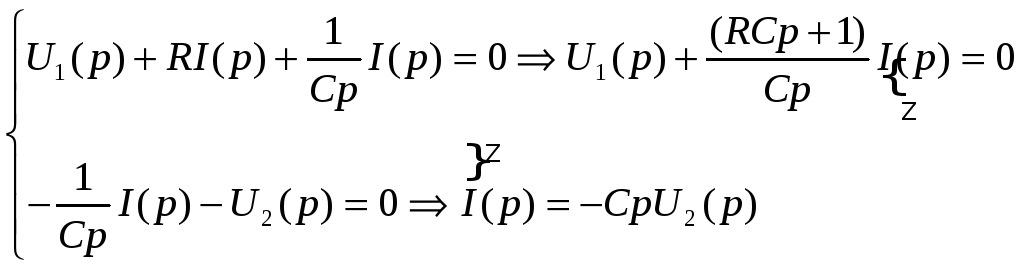 (2)
(2)
-
Исключив
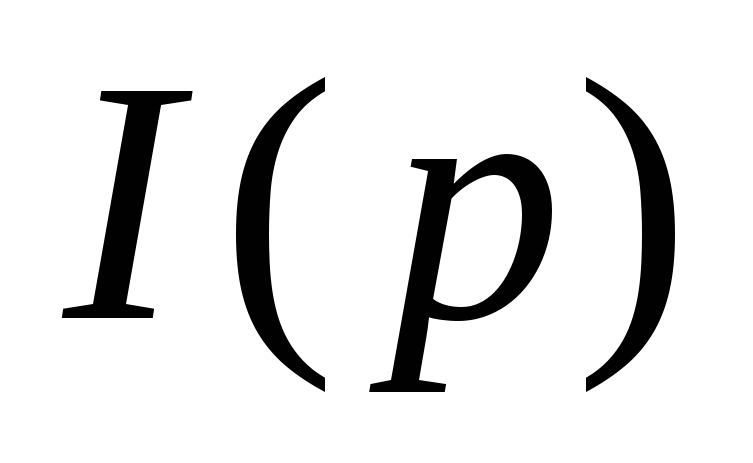 из системы уравнений (2), представим её
в виде одного уравнения, разрешенного
относительно
из системы уравнений (2), представим её
в виде одного уравнения, разрешенного
относительно
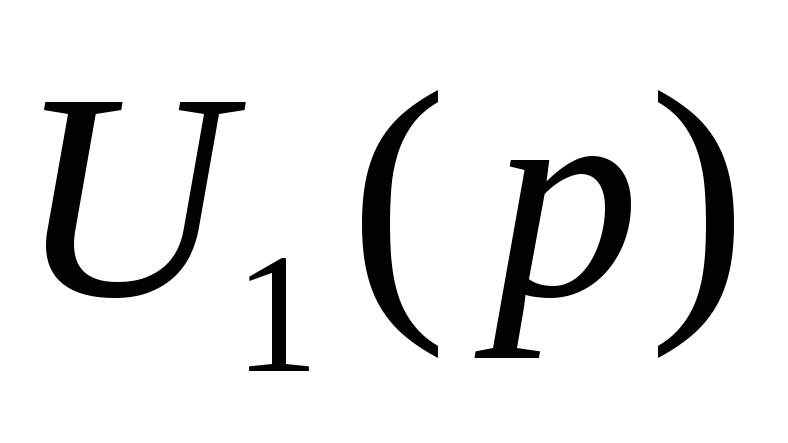 и
и
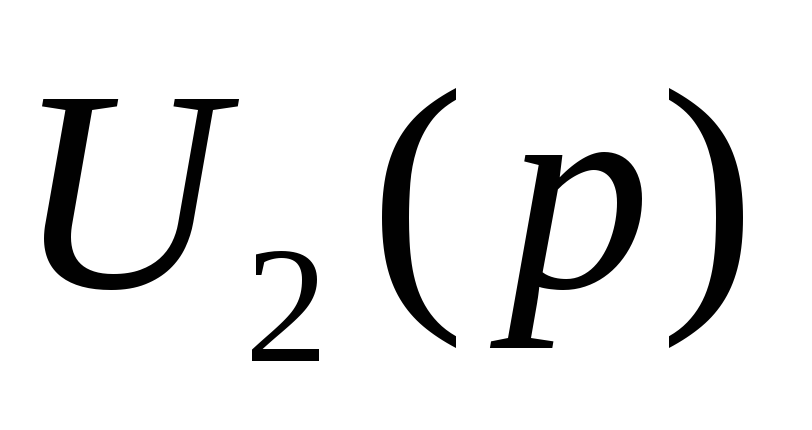
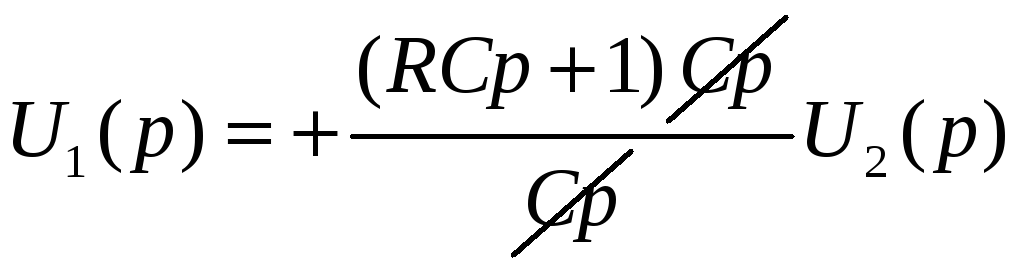 .
.
-
Руководствуясь определением передаточной функции (cм. Л 2), определим аналитическое выражение
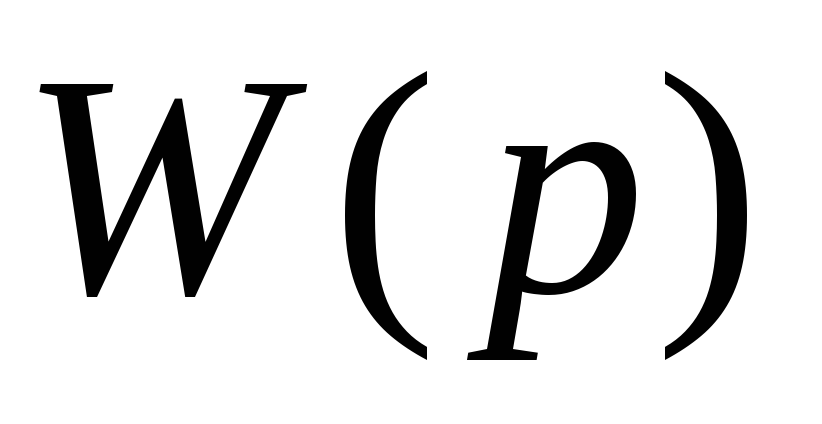
![]() .
.
Введем обозначение
коэффициента усиления
![]() и постоянной времени цепи
и постоянной времени цепи
![]() ,
тогда
,
тогда
![]() .
.
-
Статическую характеристику корректирующей цепи можно получить из выражения
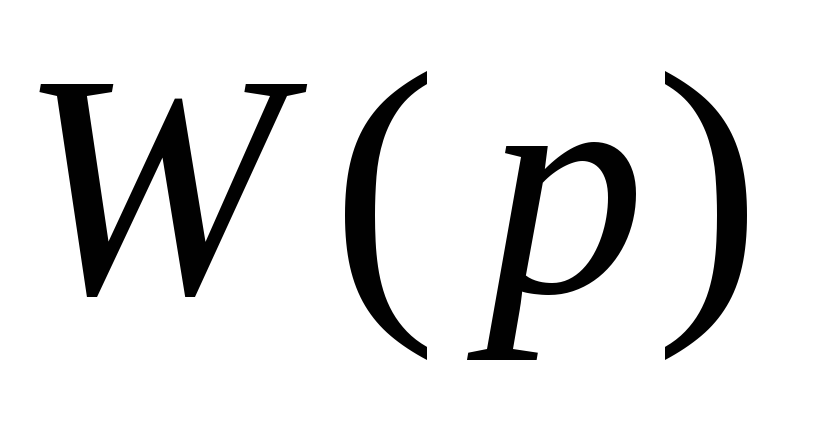 ,
положив
,
положив
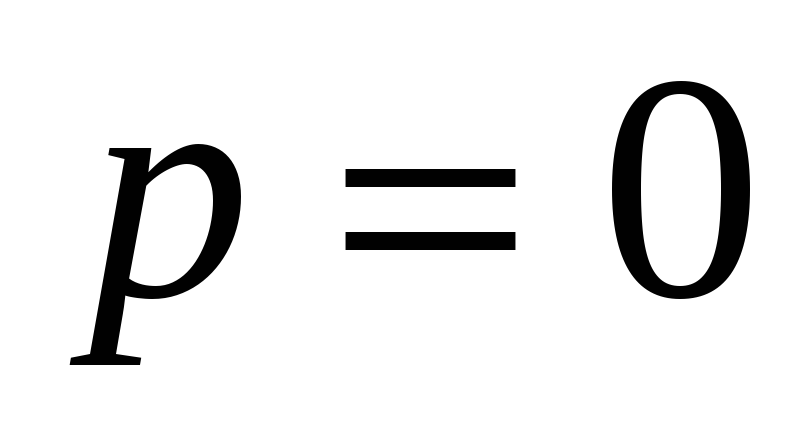
![]()
-
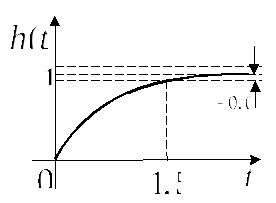
Аналитическое выражение переходной функции
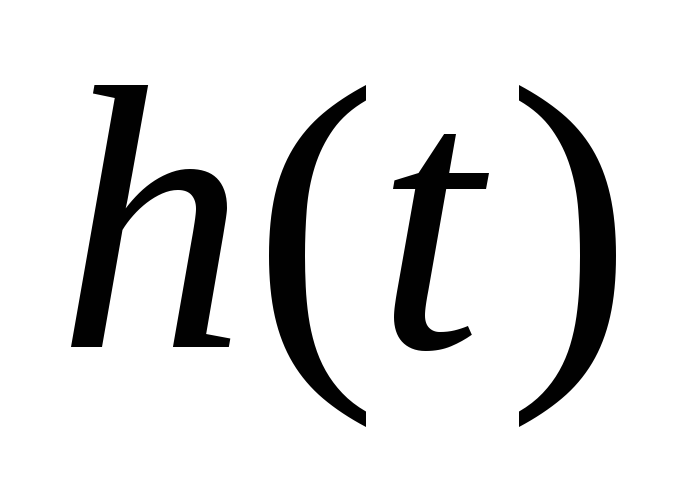 корректирующей цепи можно получить из
выражения передаточной функции
корректирующей цепи можно получить из
выражения передаточной функции
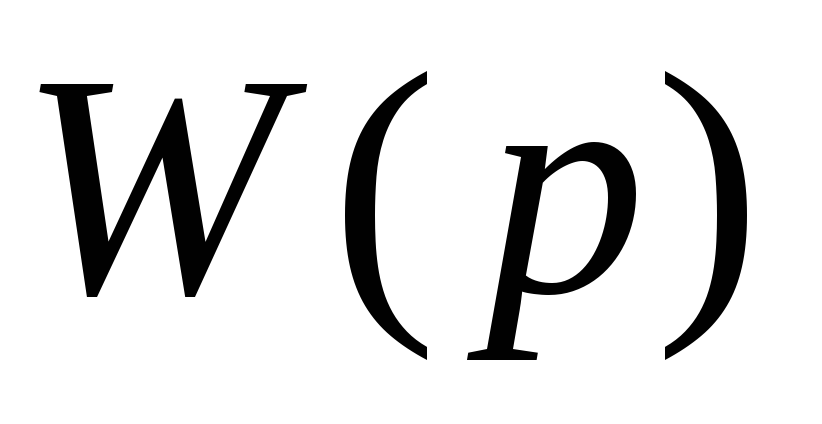
![]() .
.
-
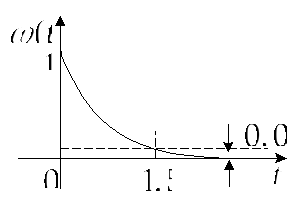
Аналитическое выражение весовой функции
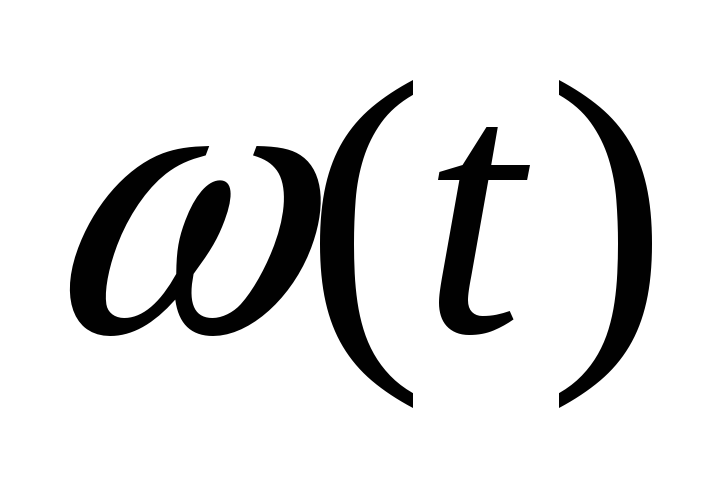 корректирующей цепи можно также получить
из выражения передаточной функции
корректирующей цепи можно также получить
из выражения передаточной функции
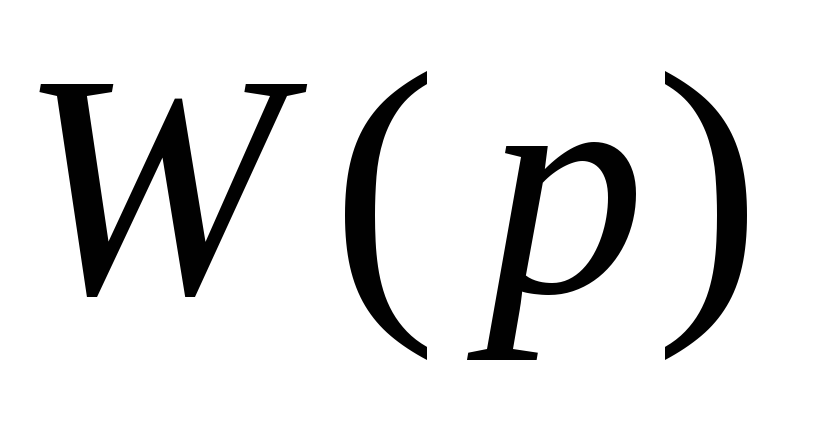
![]() .
.
-
Частотные характеристики получают из выражения
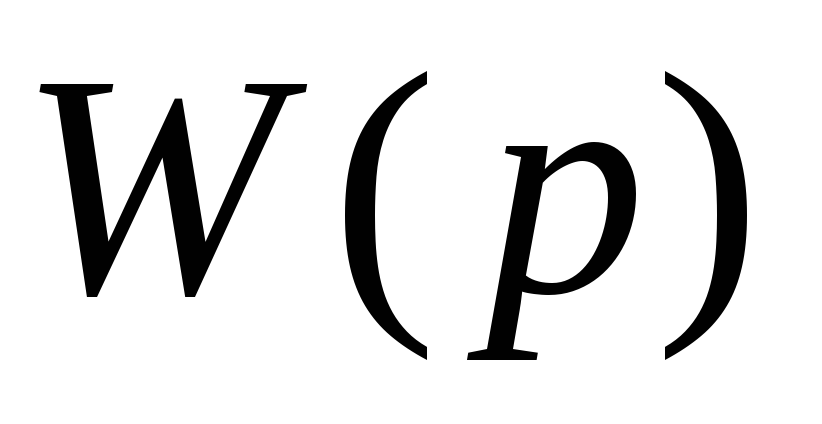 ,
предварительно выполнив замену
,
предварительно выполнив замену
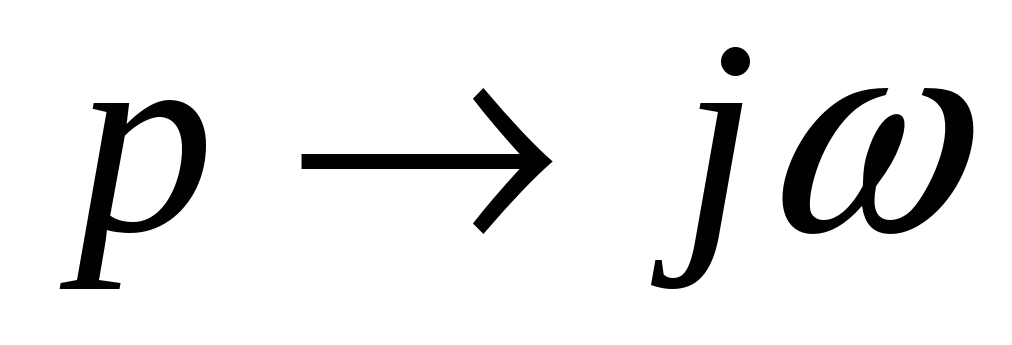 ,
избавившись от комплексного числа в
знаменателе
,
избавившись от комплексного числа в
знаменателе
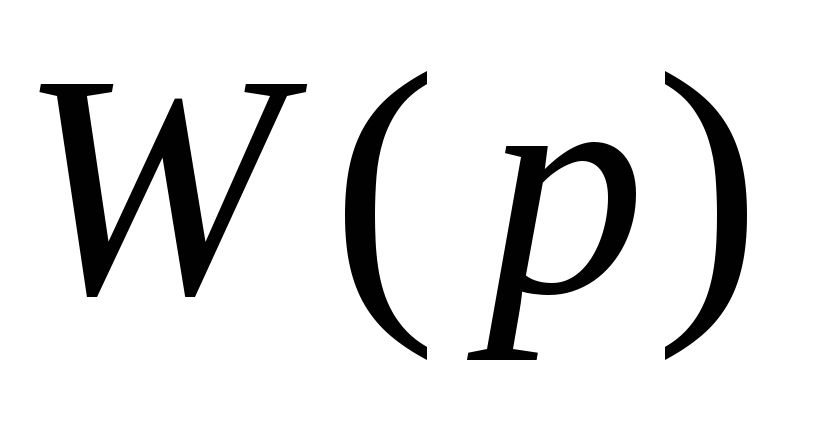 и разделив действительную и мнимую
составляющие
и разделив действительную и мнимую
составляющие
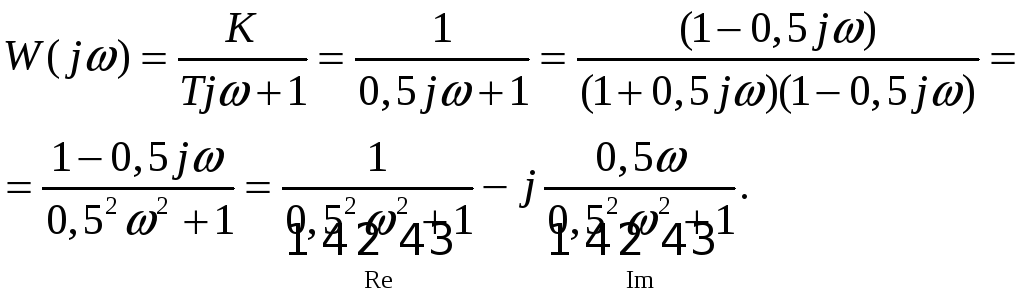
-
АФЧХ или годограф
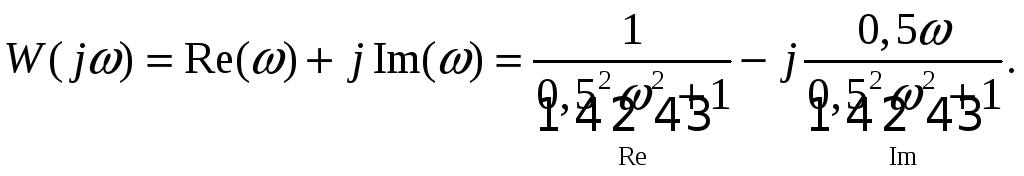
-
Ачх
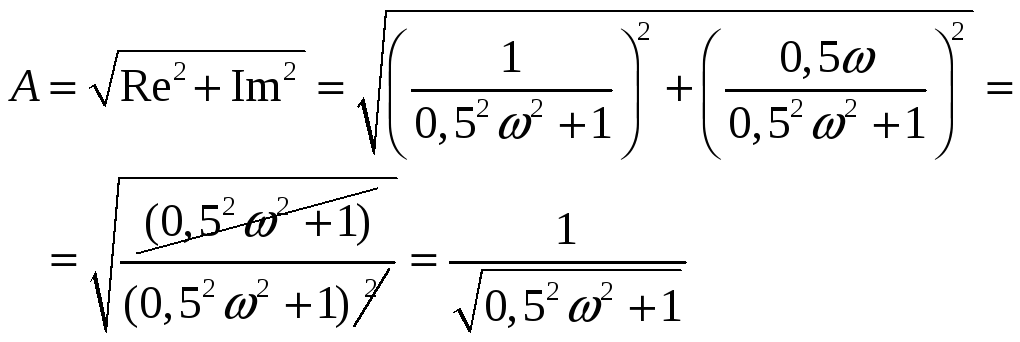
-
ФЧХ
![]() .
.
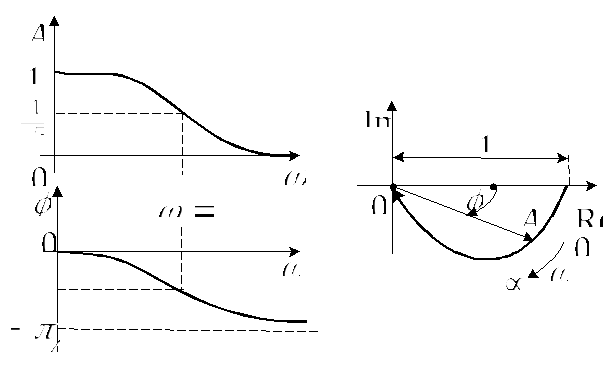
Амплитудно-фазочастотные характеристики
-
ЛАЧХ
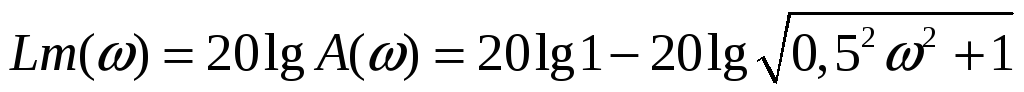
-
ЛФСХ
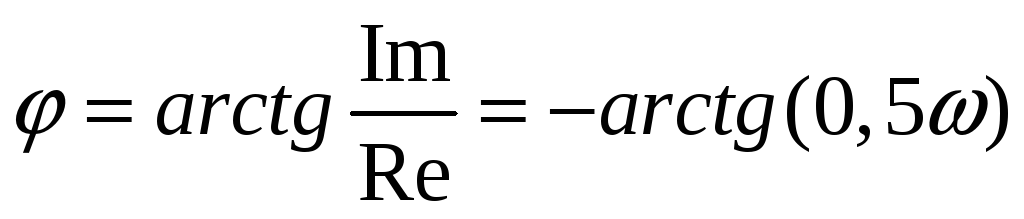
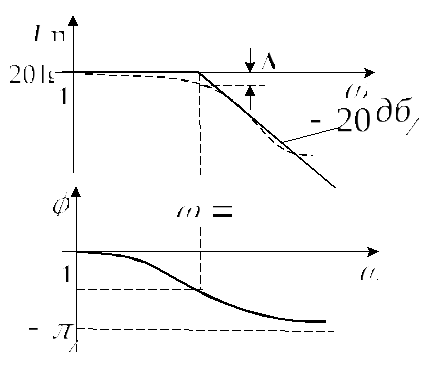
ЛАЧХ и ЛФЧХ апериодического звена
-
Пример Вывод передаточной функции
 -цепи
второго порядка
-цепи
второго порядка
Дано. принципиальная схема корректирующей цепи
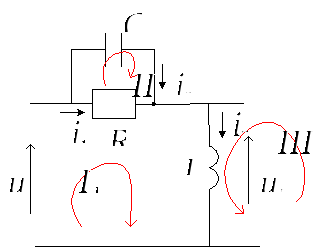
Таблица номиналов
|
|
|
|
|
|
|
|
Требуется
определить передаточную функцию
![]() корректирующей цепи двумя способами:
корректирующей цепи двумя способами:
-
используя правила Кирхгофа;
-
используя матрицу проводимостей*.
Решение I способом
-
На основе I и II правил Кирхгофа составим систему уравнений
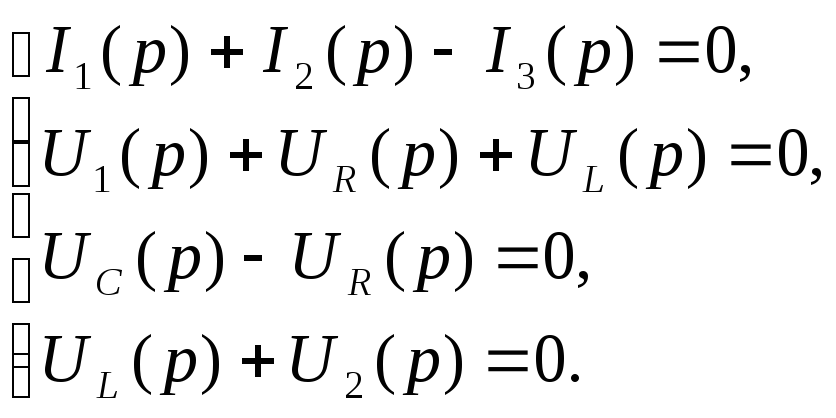 (1)
(1)
С учетом того, что
падение напряжения на элементах цепи
равны соответственно
![]() ,
,
![]() ,
,
![]() ,
перепишем систему уравнений (1) в виде
,
перепишем систему уравнений (1) в виде
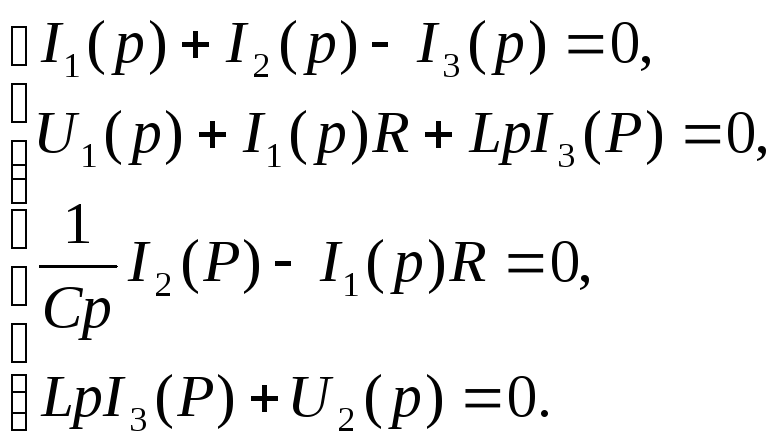 (2)
(2)
-
Представим систему уравнений (2) в виде одного уравнения, разрешенного относительно
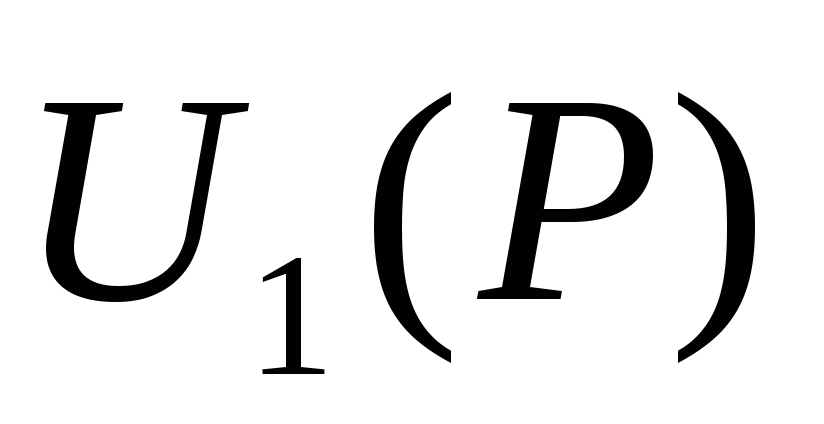 и
и
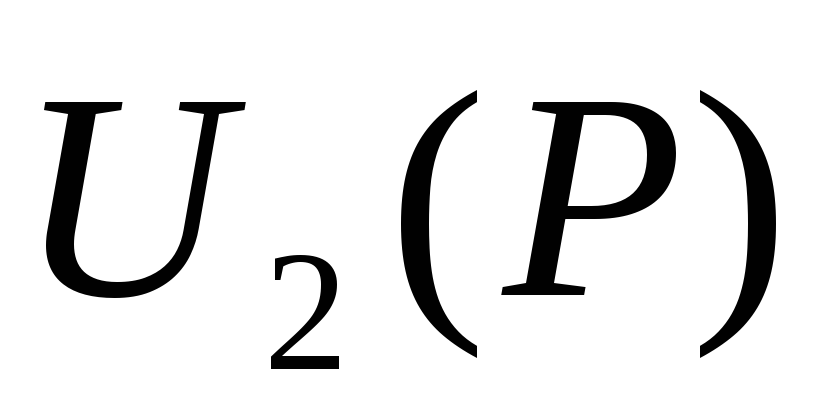
![]() (3)
(3)
-
Вывод передаточной функции из уравнения (3)
![]() . (4)
. (4)
Разделим каждое
слагаемое в (4) на
![]() ,
получим
,
получим
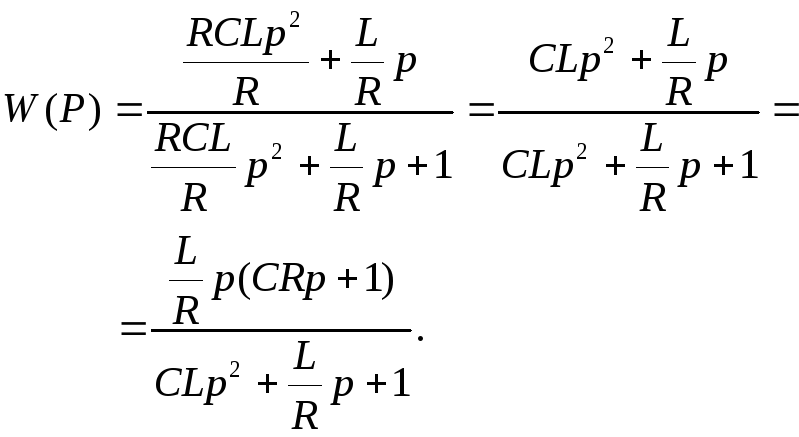 (5)
(5)
Введем следующие обозначения постоянных времени
![]() ,
,
![]() ,
,
тогда передаточная функция примет «стандартный» вид
![]() , (6)
, (6)
где
![]() ,
,
![]() .
.
Подставим численные
значения
![]() и
и
![]() выражение (6)
выражение (6)
![]()
Примечания
-
I-й закон Кирхгофа. алгебраическая сумма токов в узле равна нулю.
-
II-й закон Кирхгофа. алгебраическая сумма падений напряжений в замкнутом контуре равна нулю.
-
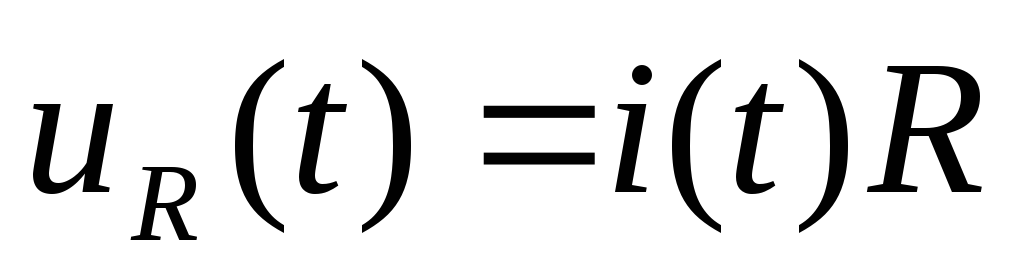 ,
,
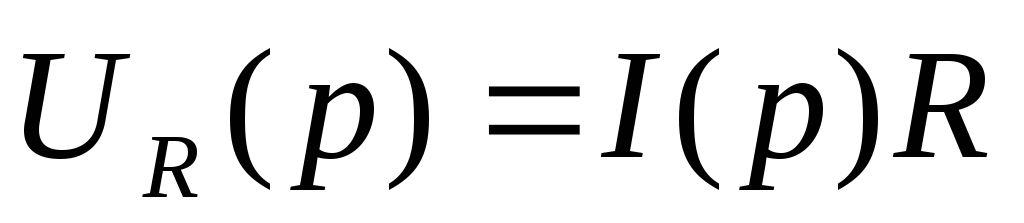 ,
,
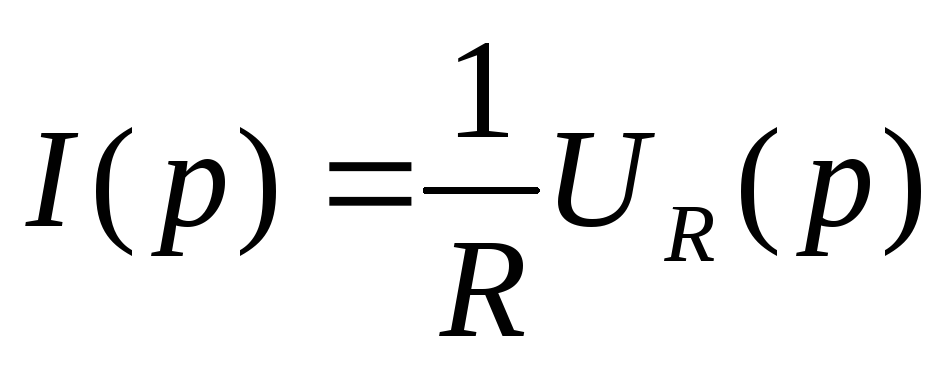 ,
,
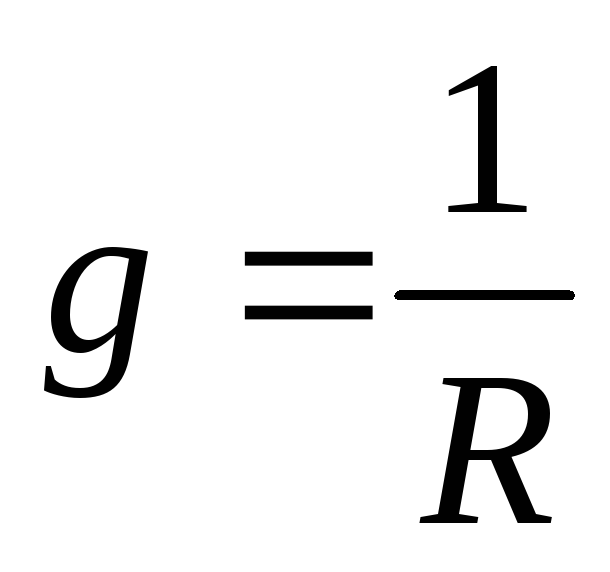 .
. -
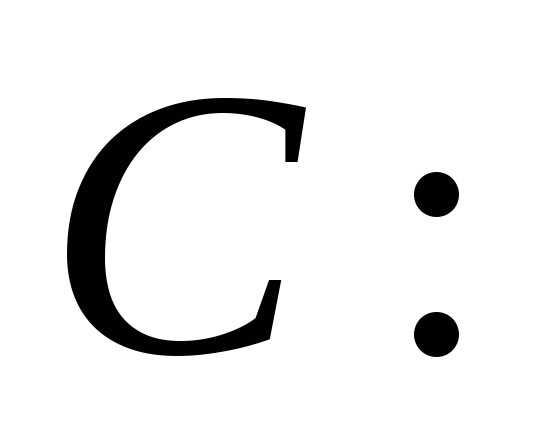
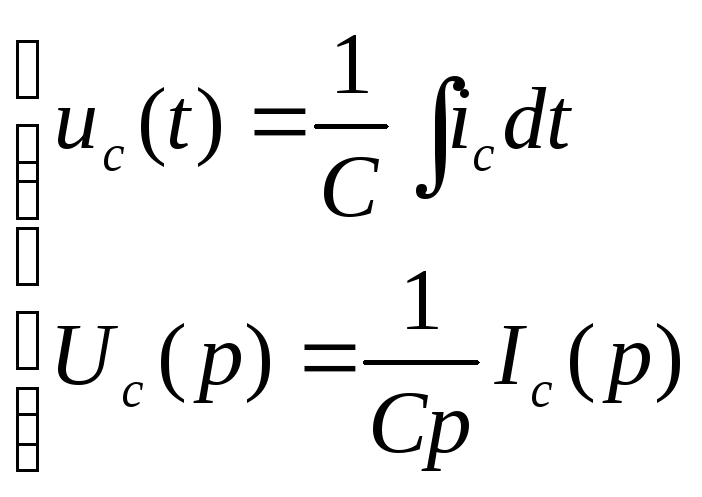 ,
,
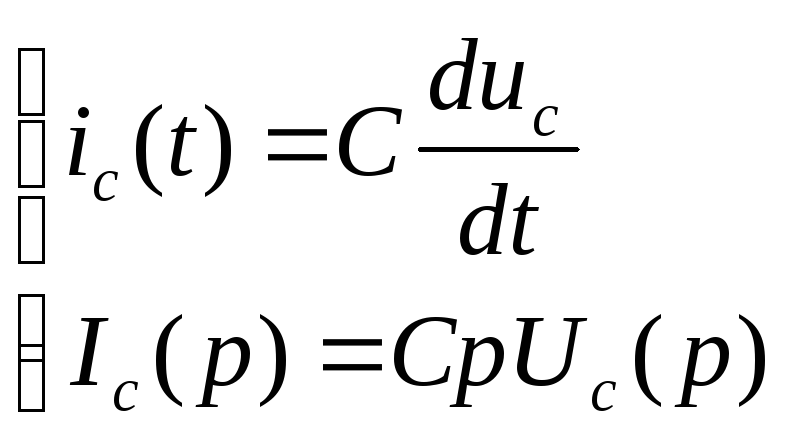 ,
,
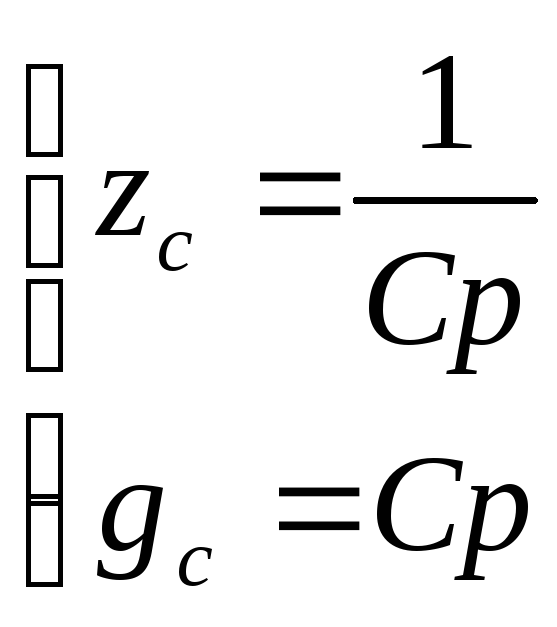 .
. -
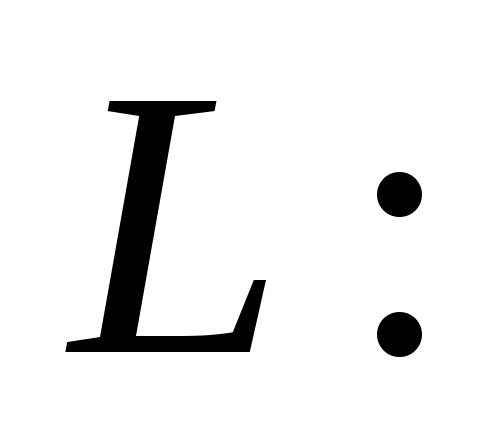
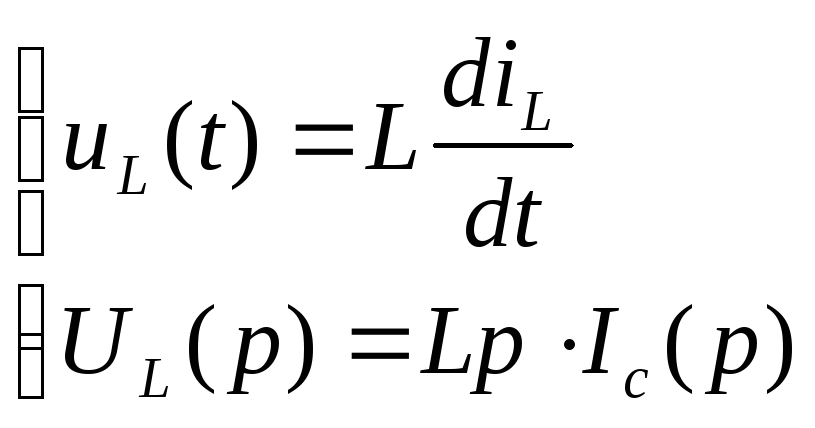 ,
,
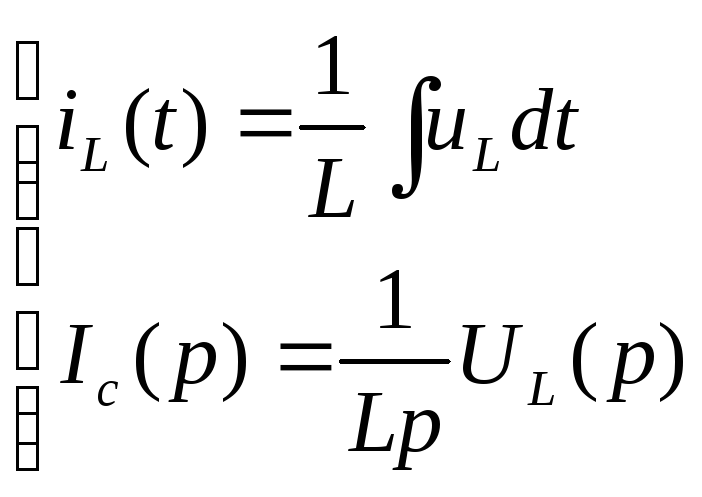 ,
,
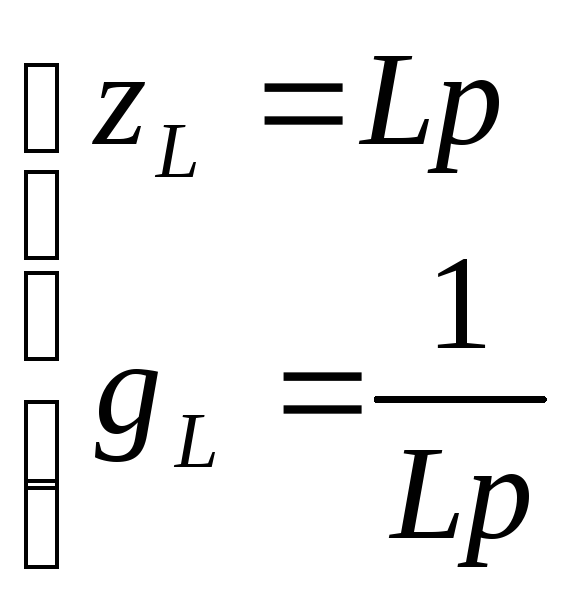 .
. -
Размерности
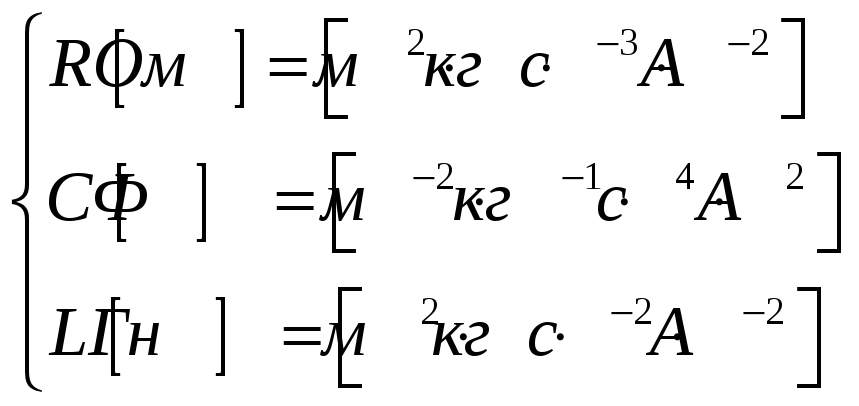 ,
,
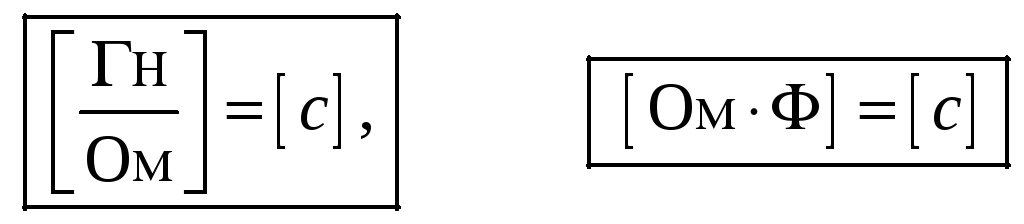 .
.
Решение II способом* (P.S. для желающих изучить)
-
Расставим номера узлов в принципиальной схеме
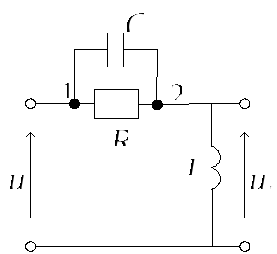
-
составить матрицу проводимостей для каждого узла
1
2
1
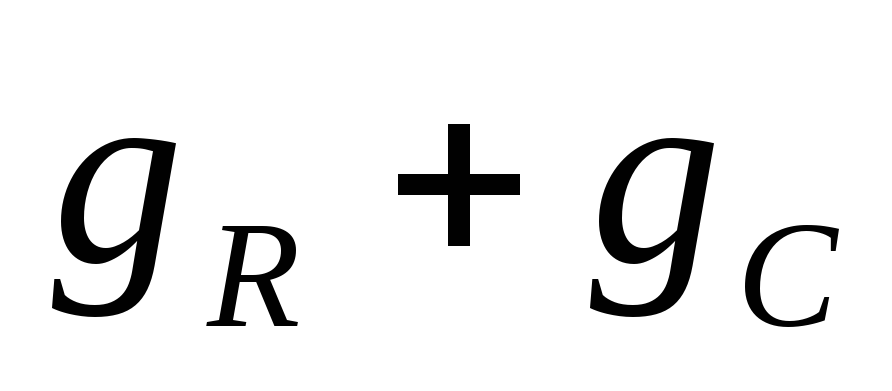
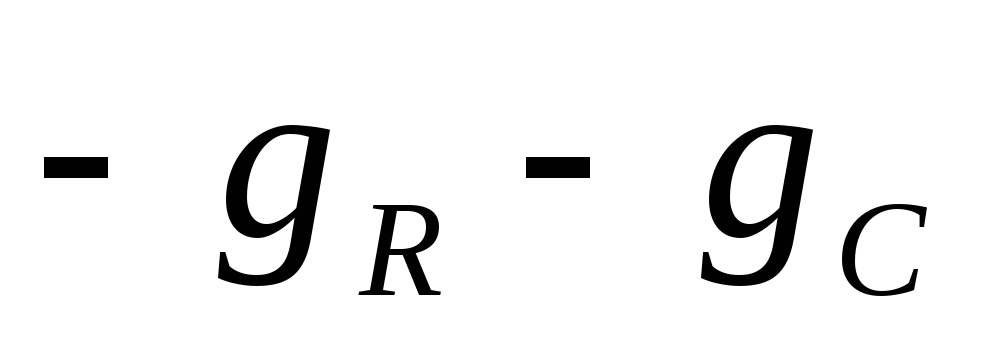
2
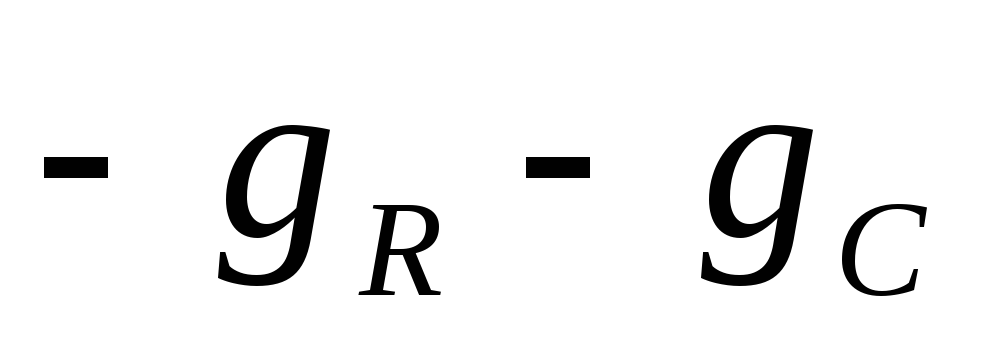
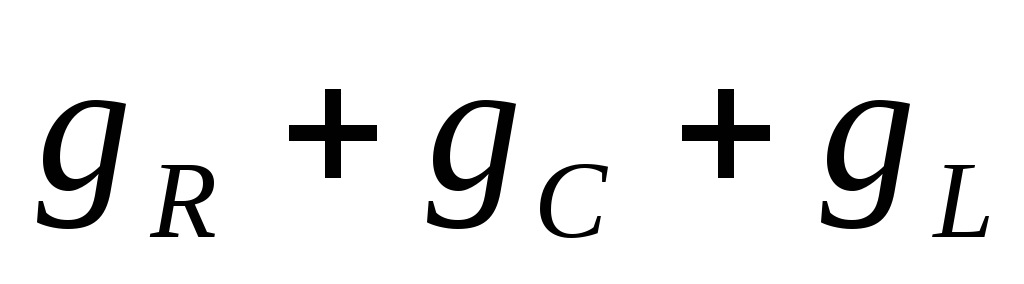
-
Определим проводимость на входе схемы
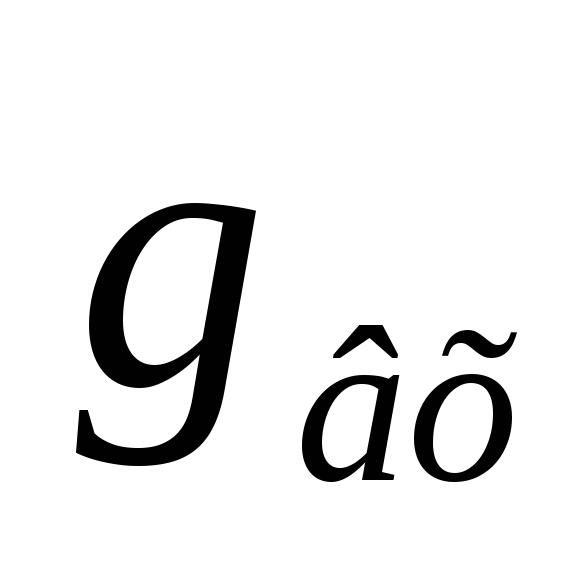 посредством вычеркивания первой строки
и первого столбца в матрице проводимостей
посредством вычеркивания первой строки
и первого столбца в матрице проводимостей
![]() .
.
-
Определим проводимость на выходе схемы
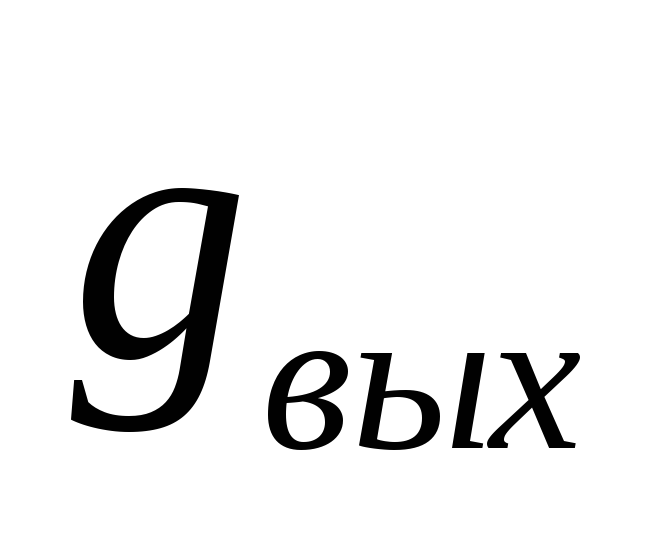 вычеркиванием первой строки и второго
столбца в матрице проводимостей
вычеркиванием первой строки и второго
столбца в матрице проводимостей
![]() .
.
-
Вывод передаточной функции
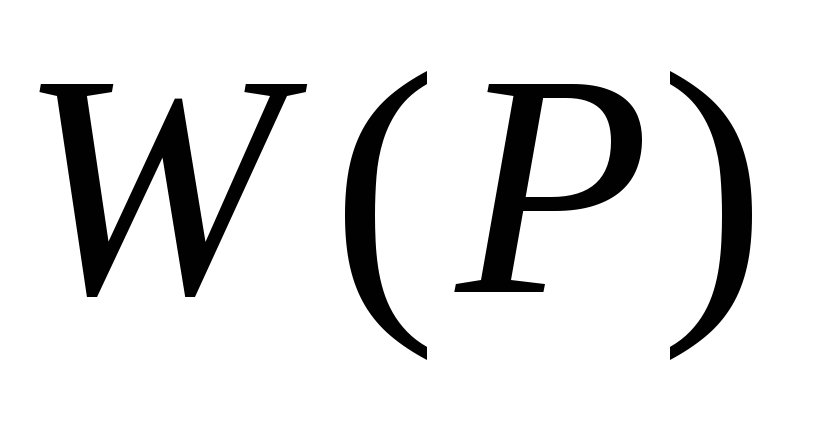

Примечание
знак
минус перед передаточной функцией
![]() говорит о том, что корректирующая цепочка
инвертирует входной сигнал. Для
исследования динамических свойств
корректирующей цепи знак минус перед
говорит о том, что корректирующая цепочка
инвертирует входной сигнал. Для
исследования динамических свойств
корректирующей цепи знак минус перед
![]() не учитывают.
не учитывают.
-
Вывод аналитических выражений динамических и частотных характеристик звена и построение соответствующих графиков.
Примечание. Если схема имеет, предположим, вид,
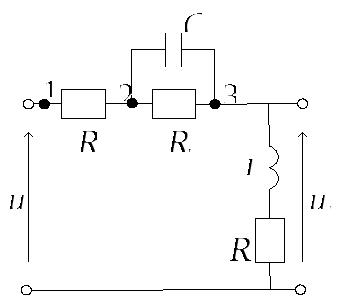
то, узлы проставляются на схеме как показано на рисунке. а проводимость участка цепи с последовательным соединением звеньев равна
![]() .
.
Матрица проводимостей будет иметь вид
|
|
1 |
2 |
3 |
|
1 |
|
|
0 |
|
2 |
|
|
|
|
3 |
0 |
|
|
Далее определяется
проводимость на входе схемы
![]() вычеркиванием первой строки и первого
столбца в матрице проводимостей
вычеркиванием первой строки и первого
столбца в матрице проводимостей
![]() .
.
проводимость
на выходе схемы
![]() определяется вычеркиванием первой
строки и третьего столбца в матрице
проводимостей
определяется вычеркиванием первой
строки и третьего столбца в матрице
проводимостей
![]() .
.
Выражение
передаточной функции по-прежнему можно
определить как отношение выходной
проводимости к входной проводимости в
операторной форме при нулевых начальных
условиях
![]() .
.
Ответ:
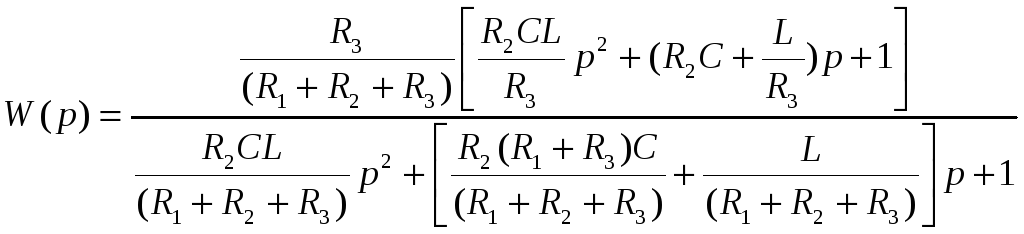 где
где
![]() – коэффициент усиления
– коэффициент усиления
![]() ,
,
![]() – постоянная
времени
– постоянная
времени
![]() ,
,
![]() – постоянная
времени
– постоянная
времени
![]() ,
,
![]() – постоянная
времени
– постоянная
времени
![]() ,
,
![]() – постоянная
времени
– постоянная
времени
![]() .
.
С учетом принятых обозначений передаточная функция примет вид
![]() .
.
-
Решение 2го примера в среде Mat cad
-
Пример. Вывод передаточной функции апериодического звена первого порядка
Структурная схема
апериодического звена первого порядка,
содержащая идеальный усилитель,
представлена на рисунке. Для идеального
усилителя справедливы следующие
допущения
![]()
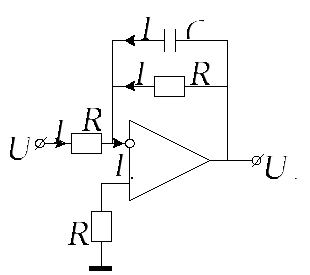
Рис. Структурная схема
Согласно I-у закону Кирхгофа сумма токов на входе операционного усилителя равна
![]() ,
,
где
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
тогда
![]() или
или
![]() ,
,
где
![]() –
коэффициент усиления усилителя,
–
коэффициент усиления усилителя,
![]() –
постоянная времени
усилителя.
–
постоянная времени
усилителя.
В операторной форме записи
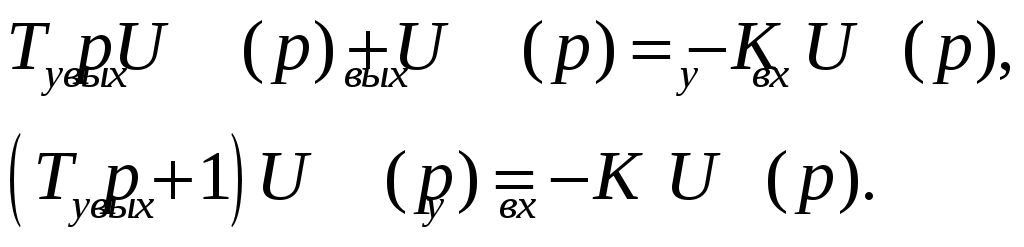
следовательно, передаточная функция примет вид
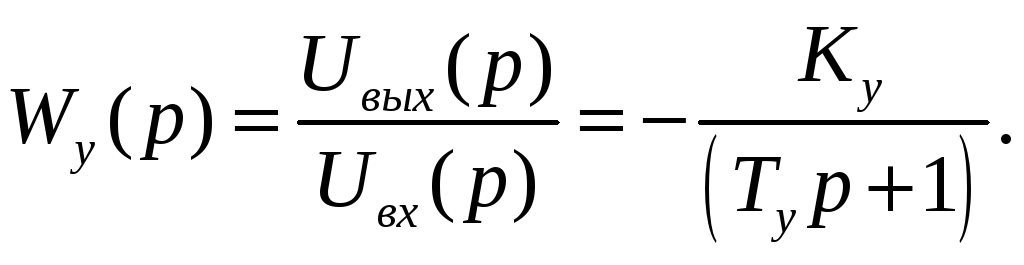
Работа в аудитории
Дано. принципиальная схема корректирующей цепи
|
|
|
|
|
|
|
|
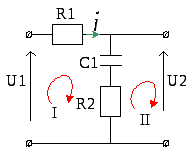
Требуется
определить передаточную функцию
![]() ,
исследовать статические, динамические
и частотные свойства корректирующей
цепи.
,
исследовать статические, динамические
и частотные свойства корректирующей
цепи.
