- •Национальный Технический Университет Украины «Киевский Политехнический Институт»
- •РАсчет Замкнутой системы iiIпорядка Структурная схема
- •1.Составить математическую модель сау
- •2.Получить дифференциальное уравнение относительно выхода по задающему и возмущающему воздействиям
- •3.Определить передаточную функцию системы.
- •3.3. Передаточную функцию замкнутой системы по ошибке при действии задающего воздействия и равенстве 0 возмущающего воздействия
- •3.4. Передаточную функцию замкнутой системы по ошибке при действии возмущающего воздействия и равенстве 0 задающего воздействия
- •4.Вычислить временные характеристики
- •4.2.С помощью обратного преобразования Лапласа найти переходную и весовую функции
- •5.Частотные характеристики
- •5.1.Афчх
- •5.4.Логорифмитическая амплитудно-частотная характеристика
- •6.Произвести анализ устойчивости сау:
- •6.1.Критерий Вышнеградского
- •6.2.Критерий Рауса-Гурвица
- •6.3.Критерий Михайлова
- •6.4.Критерий Найквиста
- •Определение устойчивости по лачх
5.Частотные характеристики
5.1.Афчх
Т.к.
Y(s)
= G(s)* -
MH(s)*
-
MH(s)*
то, передаточная функция САУ по задающему воздействию:
W(s)
=
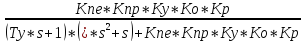 =
=

Подставим s=j*ω, тогда получим частотную характеристику :
W(j*ω)
=
 =
=
 =
=
=
 =
=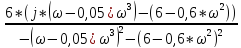 =
=
=
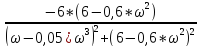 - j*
- j*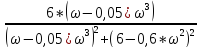
Таким образом получили АФЧХ системы:
W(j*ω)
=
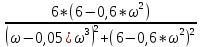 - j*
- j*
где
U(ω)
= ReW(j*ω)
=
 -
действительная
частотная характеристика
-
действительная
частотная характеристика
V(ω)
= ImW(j*ω)
=
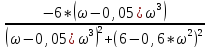 –
мнимая
частотная характеристика
–
мнимая
частотная характеристика
|
ω |
U(ω) |
V(ω) |
|
0 |
1 |
0 |
|
1 |
1.078 |
-0.19 |
|
4 |
-1.588 |
-0.353 |
|
5 |
-0.654 |
0.091 |
|
6 |
-0.351 |
0.108 |
|
7 |
-0.216 |
0.094 |
|
∞ |
→ 0 |
→ 0 |

График АФЧХ
5.2.АЧХ
Амплитудно – частотная характеристика :
А(ω)
=
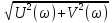
A(ω)
=
 =
=
=
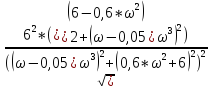 =
=
A(ω)
=
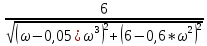
|
ω |
A(ω) |
|
0 |
1 |
|
1 |
1.094 |
|
5 |
0.66 |
|
10 |
0.089 |
|
20 |
0.013 |
|
|
→ 0 |

График АЧХ
5.3.ФЧХ
ФЧХ системы определяется за формулой:
φ(ω)
= -arctg (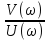 )
)
φ(ω)
= arctg(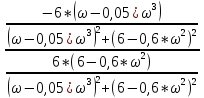 )
= -arctg(
)
= -arctg(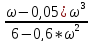 )
)
φ(ω)
= -arctg(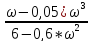 )
)
|
ω |
φ(ω), град |
|
0,1 |
89.045 |
|
1 |
80.022 |
|
5 |
-2.282 |
|
10 |
-33.192 |
|
20 |
-55.607 |
|
|
→ -90 |
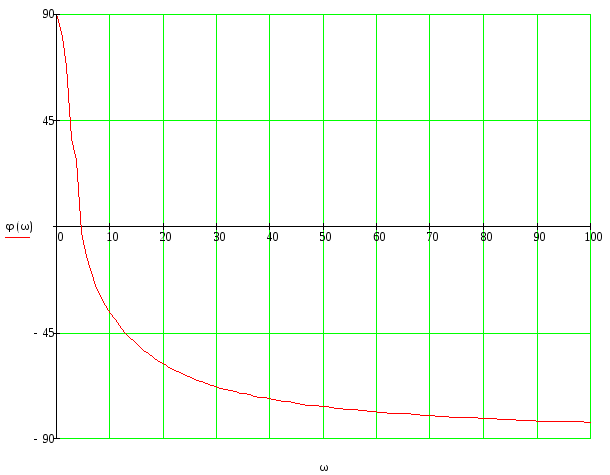
График ФЧХ
5.4.Логорифмитическая амплитудно-частотная характеристика
ЛАЧХ определяется за формулой :
L(ω) = 20 * lg(A(ω))
L(ω)
= 20*lg(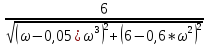 )
= 20*lg(6) – 10*lg(
)
= 20*lg(6) – 10*lg( )
)
|
ω, с-1 |
L(ω), Дб |
|
0.01 |
7.48*10-5 |
|
0.1 |
7.483*10-3 |
|
1 |
0.783 |
|
10 |
-20.985 |
|
100 |
-78.461 |
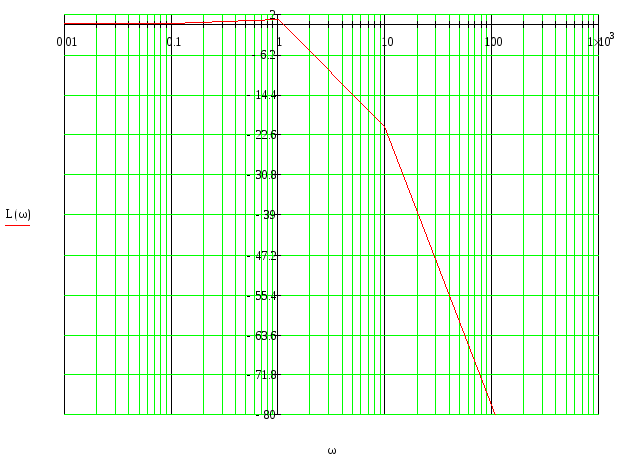
График ЛАЧХ
6.Произвести анализ устойчивости сау:
6.1.Критерий Вышнеградского
Передаточная функция замкнутой системы равна:
W(s)
=
 , тогда
характеристическое уравнение
, тогда
характеристическое уравнение
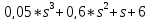 =
0 <=>
=
0 <=>
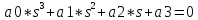 , где
, где
а0=0,05 ; а1=0,6 ; а2=1 ; а3=6
а0 , а1 , а2 , а3 > 0 - выполняется
а2*а1 > а3*а0 т.е. 0,6 > 0,3
Чтоб судить об устойчивости системы за критерием Вышнеградского, необходимо, выполнялись 2 пункта, что выполняется в данном случае.
Поэтому, за данным критерием система устойчива.
6.2.Критерий Рауса-Гурвица
Система устойчива, если действительные части всех корней характеристического уравнения – отрицательны. Тогда, в соответствии с критерием Рауса – Гурвица, для того, чтоб действительные части корней хар-го уравнения
b0*xm+b1*xm-1+b2*xm-2+…+bm-1*x+bm = 0
с действительными коэффициентами и b0 > 0 , были отрицательными, необходимо и достаточно, чтобы были положительны все определители Δ1, Δ2, … Δm :
 =
0
=
0
b0=0,05 ; b1=0,6 ; b2=1 ; b3=6
Δ3
=
 = 0,6*1*6-0,05*62=1,8
= 0,6*1*6-0,05*62=1,8
Δ2
=
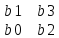 =
= = 0,6 + 6*0,05 = 0,9
= 0,6 + 6*0,05 = 0,9
Δ1 = 0,6
Т.к. условие устойчивости b0, b1, b2, b3 > 0 выполняется и Δ1, Δ2, Δ3 > 0 , то система устойчива
6.3.Критерий Михайлова
Характеристический полином замкнутой САУ :
D(s)
=

Подставим S=j*ω и определим действительную и мнимую части :
D(j*ω)
=
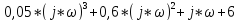 =
= =
=
=
 ,тогда
,тогда
U(ω)
= Re D(j*ω) =

V(ω)
= Im D(j*ω) =

|
ω |
U(ω) |
V(ω) |
|
0 |
6 |
0 |
|
1 |
5.4 |
0.95 |
|
2 |
3.6 |
1.6 |
|
3 |
0.6 |
1.65 |
|
5 |
-9 |
-1.25 |
|
∞ |
-∞ |
-∞ |
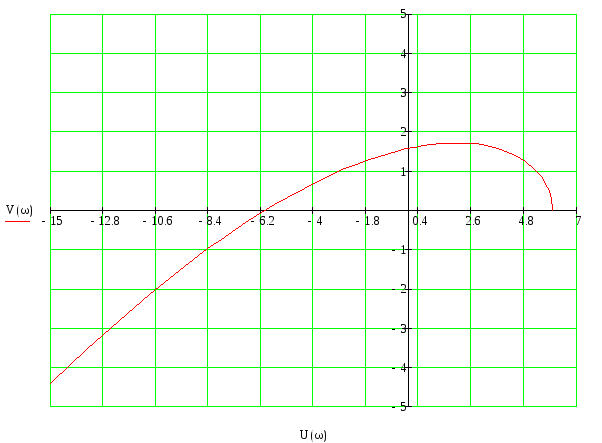
Годограф Михайлова
Для устойчивости САУ необходимо и достаточно, чтобы годограф Михайлова, начинаясь при ω=0 на вещественной положительной полуоси, с ростом частоты ω от 0 до ∞ обходил последовательно в положительном направлении n квадрантов комплексной плоскости.
В нашем случае годограф начинается положительной вещественной полуоси, и проходит последовательно 3 квадранта и в последнем уходит в бесконечность, следовательно система устойчива