Коэффициент корреляции

Коэффициент корреляции между выборочными величинам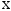и и 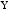определяется в виде:

, , .

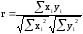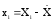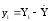Возводя коэффициент корреляции в квадрат, получаем коэффициент детерминации:

.

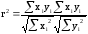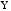Поскольку наклон линии регрессии между и равен 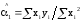, то

.

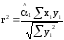Так как 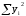будет общей вариацией зависимой переменной 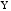, и, кроме того, 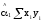есть вариация, объясняемая линейной регрессией 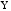по 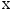. Коэффициент детерминации представляет ту долю общей вариации зависимой переменной, которую объясняет регрессия. Коэффициент 1-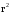 часто называют коэффициентом неопределенности, он представляет ту долю общей вариации зависимой переменной, которую регрессия не объясняет.

Адекватность регрессионного уравнения

Адекватность модели – степень соответствия исходных данных и оценок, полученных при помощи регрессионного анализа. Другими словами, насколько точно регрессионная модель отражает анализируемые данные. Для проверки адекватности модели используется F критерий Фишера.

В случае расчетов вручную действует следующее правило:

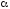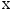Если F_р<F_т, то принимается нулевая гипотеза (H₀) с соответствующим уровнем значимости . При этом можно утверждать, что линейная зависимость между и 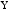отсутствует.

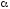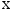Если F_р>F_т, то принимается альтернативная гипотеза (H₁) с соответствующим уровнем значимости (F_p - расчетное значение F критерия Фишера, F_т – табличное значение F критерия Фишера F_т=F(1,n-2, )). При этом можно утверждать, что линейная зависимость между и 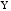присутствует.

Формула для расчета F критерия Фишера:

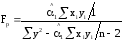, где n - число пар наблюдений.

В случае машинной обработки при помощи системы MINITAB для WINDOWS для принятия решения используем следующее правило:

Если P < 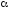, то нулевая гипотеза отвергается и принимается альтернативная при соответствующем уровне значимости .

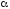Если P > 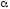, то альтернативная гипотеза отвергается и принимается нулевая при соответствующем уровне значимости .

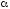2 Регрессионный анализ в системе minitab.

Для проведения регрессионного анализа необходимо:

1) ввести данные .

2) Stat > Regression>Regression – позволяет выполнить простую или множественную регрессию (построение зависимости между откликом и переменной), и заполнить следующие ячейки:

Response – переменная отклика;

Predictors – независимые переменные;

Options – опции;

Graphs – построение графиков;

Storage – сохранение полученных результатов.

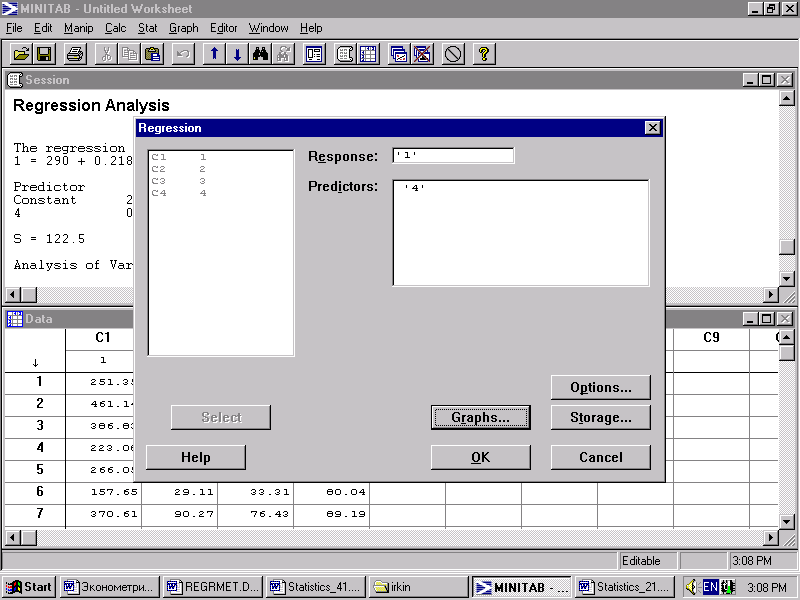
Рис. 2.1 - Команда Stat > Regression> Regression .

3) Stat > Regression > Fitted Line Plot – позволяет построить линейную, квадратическую и кубическую регрессии от одной переменной.

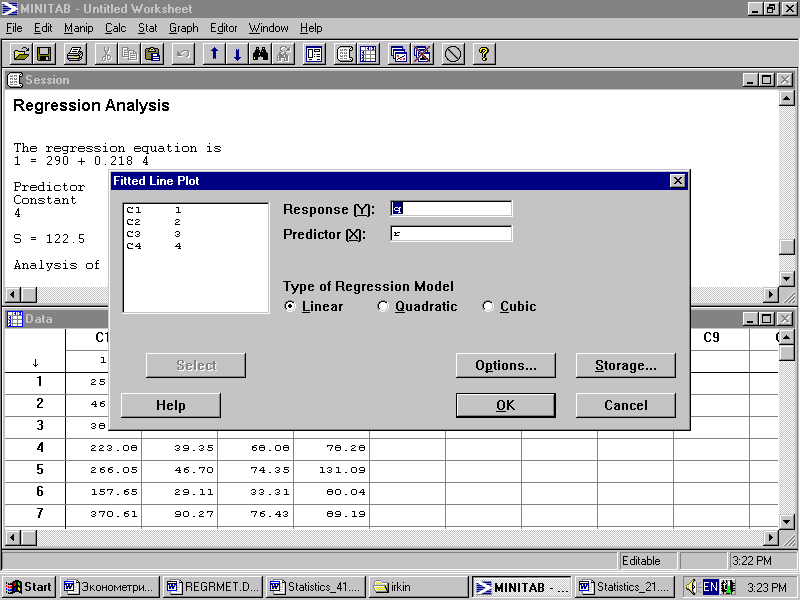
Рис. 2.2 Команда Stat > Regression > Fitted Line Plot

Пункты диалогового окна:

Response [Y] - переменная отклика или независимая переменная.

Predictor [X] - независимая переменная.

Type of Regression Model

Linear - модель линейной регрессии.

Quadratic - модель квадратичной регрессии.

Cubic - модель кубической регрессии.

3. Пример регрессионного анализа

Проблема. Менеджеру фирмы необходимо проверить действенность рекламы (число показов в месяц) на продажи изделий фирмы.

Таблица 3.1 – Данные для анализа

Продажа (тыс.штук), Y	Реклама (число показов в месяц), X
260.3	5
286.1	7
279.4	6
410.8	9
438.2	12
315.3	8
565.1	11
570	16
426.1	13
315	7
403.6	10
220.5	4
343.6	9
644.6	17
520.4	19
329.5	9
426	11
343.2	8
450.4	13
421.8	14