
- •Методические указания
- •Содержание
- •Общие понятия регрессионного анализа.
- •Коэффициент корреляции
- •Адекватность регрессионного уравнения
- •2 Регрессионный анализ в системе minitab.
- •Пример регрессионного анализа
- •Ход решения проблемы
- •Задание по выполнению лабораторной работы
- •Порядок выполнения работы
- •Контрольные вопросы
- •Библиография
Министерство
образования и науки Украины 




Севастопольский национальный технический университет
Методические указания
к выполнению лабораторной работы №5
”Однофакторный регрессионный анализ при помощи
системы MINITAB для WINDOWS “
по учебной дисциплине
«Прикладная статистика»
для студентов экономических специальностей
всех форм обучения
Севастополь
2004
УДК 658.
Однофакторный регрессионный анализ при помощи системы " MINITAB" для WINDOWS. Методические указания по выполнению лабораторной работы №4 по дисциплине "Прикладная статистика" / Сост. Д.В. Филатова, И. А. Гребешкова Б.А. Букач - Севастополь: Изд-во СевГТУ, 2000. - 14с.
Целью методических указаний является применение теоретических знаний по теме "Одномерный регрессионный анализ" при решении ситуаций с помощью системы MINITAB. Методические указания предназначены для студентов экономических специальностей.
Методические указания рассмотрены и утверждены на заседании кафедры менеджмента и экономико-математических методов, (протокол № 6 от "20" __февраля 2001 г.)
Допущено учебно-методическим центром СевГТУ в качестве методических указаний
Рецензенты:
Цуканов А.В, д.т.н., заведующий кафедры "Менеджмент и экономико-математические методы"
Персидсков Г.М. - нормоконтроль
Содержание
|
|
Стр. |
|
4 |
|
7 |
|
8 |
|
11 |
|
13 |
|
13 |
|
Библиография |
13 |
-
Общие понятия регрессионного анализа.
Регрессионный анализ предназначен для установления функциональной связи между одной зависимой переменной и одной или несколькими независимыми переменными.
Рассмотрим уравнение регрессии в случае, если устанавливается функциональная связь между зависимой переменной и одной независимой переменной.
Тогда регрессионное уравнение для линейной модели примет вид:
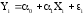 ,
где
,
где
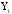 - зависимая переменная,
- зависимая переменная,
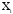 - независимая переменная,
- независимая переменная,
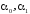 - коэффициенты регрессионного уравнения,
- коэффициенты регрессионного уравнения,
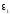 - ошибка с нормальным законом распределения,
средним равным нулю и стандартным
отклонением .
- ошибка с нормальным законом распределения,
средним равным нулю и стандартным
отклонением .
Так
как в экономике в большинстве практических
случаев сбор данных или весьма
затруднителен, или связан с большими
затратами, поэтому чаще всего каждому
значению независимой переменной
соответствует только одно наблюдение
зависимой переменной. В нашем случае
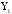 - это одно наблюдение, соответствующее
- это одно наблюдение, соответствующее
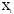 .
.
Для оценки коэффициентов регрессионного уравнения будем использовать метод наименьших квадратов (МНК). Регрессионное уравнение, коэффициенты которого оценены при помощи МНК, будет иметь вид:
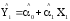 ,
где
,
где
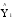 - оцененное значение,
- оцененное значение,
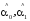 - оценки коэффициентов регрессионного
уравнения, полученные с помощью МНК,
знак ^ показывает, что это оценка случайной
величины.
- оценки коэффициентов регрессионного
уравнения, полученные с помощью МНК,
знак ^ показывает, что это оценка случайной
величины.
МНК минимизирует сумму квадратов ошибок (остатков):
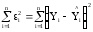 ,
где
,
где
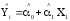 .
.
Оценки коэффициентов регрессионного уравнения, полученные при помощи метода наименьших квадратов равны:
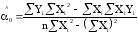 ;
;
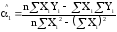 ,
,
Произведя преобразования, получаем:
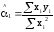
и
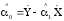 ,
где
,
где
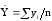 и
и
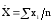 ,
где
,
где
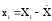 ,
,
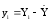 .
.
Так как в процессе определения функциональной связи между исследуемыми переменными регрессионное уравнение строится не на анализе данных генеральной совокупности, а на основе выборки, то следующим шагом анализа будет проверка значимости коэффициентов регрессионного уравнения и проверка адекватности модели.
Значимость коэффициентов регрессионного уравнения предполагает проверку семейства гипотез:
H0:
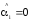 - коэффициент не значим,
- коэффициент не значим,
H1:
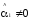 - коэффициент значим.
- коэффициент значим.
Для проверки значимости коэффициентов регрессионного уравнения используется t критерий Стьюдента. В случае расчетов вручную действует следующее правило:
Если
tр>tт,
то
принимается альтернативная гипотеза
(H1)
с соответствующим уровнем значимости
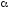 (tр
-
расчетное значение t
критерия Стьюдента, tт
–
табличное значение t
критерия Стьюдента, tт=t(n-1,
(tр
-
расчетное значение t
критерия Стьюдента, tт
–
табличное значение t
критерия Стьюдента, tт=t(n-1,
 /2)).
/2)).
Если tр<tт, то принимается нулевая гипотеза (H0).
При использовании системы MINITAB для WINDOWS для принятия решения используем следующее правило:
Если
P
<
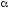 ,
то нулевая гипотеза отвергается и
принимается альтернативная при
соответствующем уровне значимости
,
то нулевая гипотеза отвергается и
принимается альтернативная при
соответствующем уровне значимости
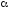 .
.
Если
P
>
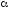 ,
то альтернативная гипотеза отвергается
и принимается нулевая гипотеза.
,
то альтернативная гипотеза отвергается
и принимается нулевая гипотеза.
