БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ

ФАКУЛЬТЕТ ИНЖЕНЕРНО-СТРОИТЕЛЬНЫЙ

КАФЕДРА УИТ

Расчетно-графическая работа №1

по дисциплине

Теория автоматического управления

Исследование устойчивости стационарных и нестационарных линейных и непрерывных и дискретно-непрерывных систем автоматического управления

Выполнил ст. гр. УИТ-41

Сербаев В.В.

Принял доцент каф. УИТ

Скоробогатова Т.Н. _______

“______” ___________2003

2003

СОДЕРЖАНИЕ

1 Техническое задание 3

2 Анализ звеньев 3

3 Упрощение 4

4 Проверка устойчивости 6

4.1 Критерий Гурвица 6

4.2 Критерий Льенара-Шипара 6

4.3 Критерий Рауса 6

4.4 Критерий Михайлова 7

4.5 Критерий Найквиста 9

4.6 D-разбиение 10

4.7 Критерий Ляпунова 12

Вывод 13

Вариант № 44

Цель работы: изучить методы исследования устойчивости стационарных и нестационарных линейных непрерывных и дискретно непрерывных САР. Доработать систему, получив ее устойчивой. Проверить устойчивость по критериям: 1.Гурвица, 2.Льенара – Шипара, 3.Рауса, 4.Михайлова, 5.Найквиста, 6.D-разбиения, 7.Ляпунова.

1 Техническое задание

И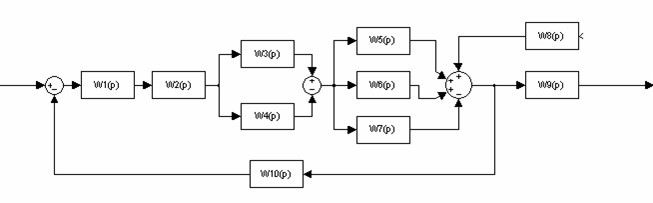сходная схема изображена на схеме 1

Схема 1

Передаточные функции звеньев:

W₁(p)=38; W₂(p)=; W₃(p)=0.74; W₄(p)=0.74; W₅(p)= ; W₆(p)= ; W₇(p)= ; W₈(p)= ; W₉(p)=16.3; W₁₀(p)=

2 Анализ звеньев

W₁(p) – пропорциональное звено, служит для усиления входного сигнала, являющегося результатом сравнения первоначального сигнала и сигнала ООС; W₂(p) – апериодическое звено, в данном случае служит для ослабления резких скачков, поступающих с усилителя; W₃(p) и W₄(p) – пропорциональные звенья, служат для ослабления сигнала поступившего с W₂(p), после чего сигналы сравниваются, на выходе получаем ноль, т.к. передаточные функции звеньев равны; W₅(p), W₆(p), W₇(p) – параллельное соединение звеньев дает одно пропорциональное звено; W₈(p) – последовательное соединение интегрирующего и апериодического звена, делает систему неустойчивой; W₉(p) – усилительный эффект на выходе, возможно дальнейшее использование сигнала; W₁₀(p) – звено обратной связи, служит для преобразования сигнала вышедшего из прямого звена, в удобную для сравнения форму, снимает резкие скачки.

3 Упрощение

Требуется изменить передаточную функцию W₃(p) или W₄(p), чтобы суммарная функция была ненулевой. Требуется добавить звено к W₈(p) ( дифференцирующее звено), чтобы снять интегрирующую составляющую, тем самым итоговое звено будет устойчивым. Проведя преобразования, получим схему 2.

Схема 2

Обозначение: W₁₁(p)=2, W₁₂(p)=p.

Упростим:

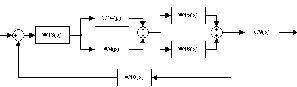
Схема 3

Обозначение: W₁₃(p)=W₁(p)*W₂(p)= 38*=

W₁₄(p)=W₁₁(p)*W₃(p)=2*0.74=1.48

W₁₅(p)=W₁₂(p)*W₈(p)=p*=

W₁₆(p)=W₅(p)+W₆(p)-W₇(p)= +-=

Упростим далее:

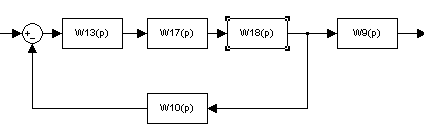
Схема 4

Обозначение: W₁₇(p)=W₁₄(p)-W₄(p)=1.48-0.74=0.74

W₁₈(p)=W₁₅(p)+W₁₆(p)= +=

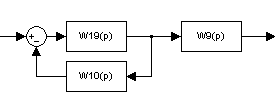
Схема 5

Обозначение: W₁₉(p)=W₁₃(p)*W₁₇(p)*W₁₈(p)= *0.74*=

=

Схема 6

Обозначение: W₂₀(p)==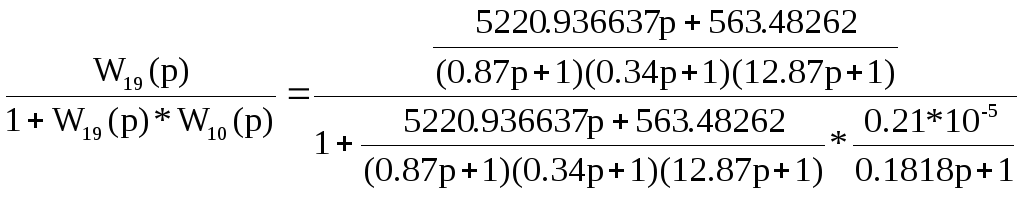

Упростим схему:

Схема 7

Обозначение: W₂₁(p)=W₂₀(p)*W₉(p)=

4 Проверка устойчивости

4.1 Критерий Гурвица

Запишем характеристическое уравнение системы:

a₀=0.692102782; a₁=6.6918393; a₂=18.428238; a₃=14.27276397; a₄=1.001183313

Теперь можно составить главный определитель Гурвица

Теперь посчитаем определители:

1. (6.6918393)= 6.6918393

2. =113.441

3. =1574

Согласно критерию Гурвица, система устойчива, т.к. определители имеют один знак с a₀=0.692102782.

4.2 Критерий Льенара-Шипара

Характеристическое уравнение является уравнением 4 степени, т.е. должно выполнятся и

. Условие выполняется, т.е. система устойчива.

4.3 Критерий Рауса

Требуется составить таблицу коэффициентов.

C_k,i=C_k+1,i-2-r_i*C_k+1,i-1, где

Коэффициент ri	Номер строки i	Номер столбца к
		к=1	к=2	к=3
-----	1	a0=C11	a2=C21	a4=C31
-----	2	a1=C12	a3=C22	a5=C32=0
r3=C11/C12= =0.103424895	3	C13=C21-r3*C22= =16.95207889	C23=C31-r3*C32= =1.001183313	C33=C41-r3*C42= =0
r4=C12/C13= =0.394750363	4	C14=C22-r4*C23= =13.87754649	C24=C32-r4*C33= =0	C34=C42-r4*C43= =0
r5=C13/C14= =1.22154726	5	C15=C23-r5*C24= =1.001183313	C25=C33-r5*C34= =0	C35=C43-r5*C44= =0

Таблица 1

Согласно критерию Рауса, система устойчива, т.к. все коэффициенты столбца 1 имеют один знак.

4.4 Критерий Михайлова

Для использования критерия требуется в характеристическом уравнении использовать преобразование p=jω. Используем данное преобразование:

D(jω)=0.692102782ω⁴-j6.6918393ω³-18.428238ω²+j14.27276397ω+1.001183313=0

Кроме того: D(jω)=X(ω)+jY(ω), тогда

X(ω)=0.692102782ω⁴-18.428238ω²+1.001183313

Y(ω)=-6.6918393ω³+14.27276397ω

Графики оформлены в MathCAD, с постепенным увеличением масштаба.

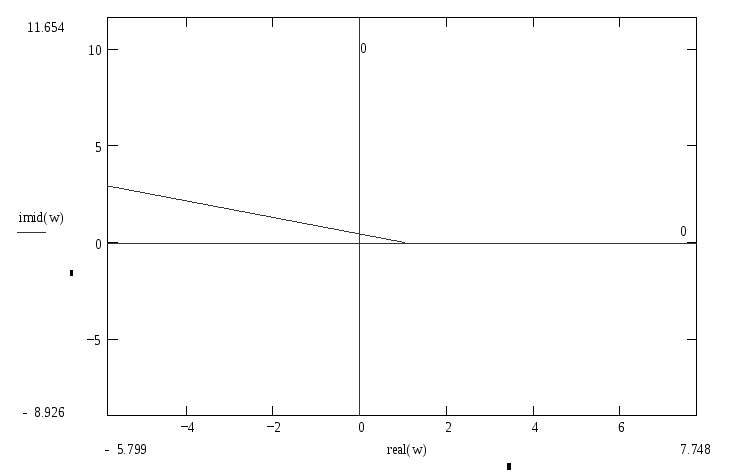
Рисунок 1, а

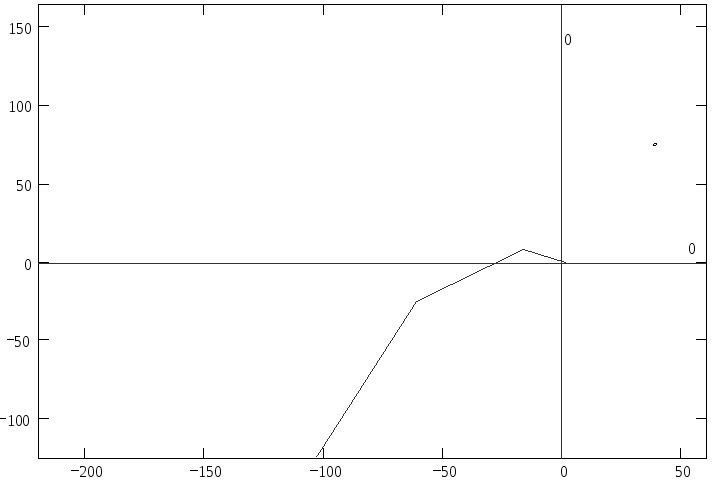
Р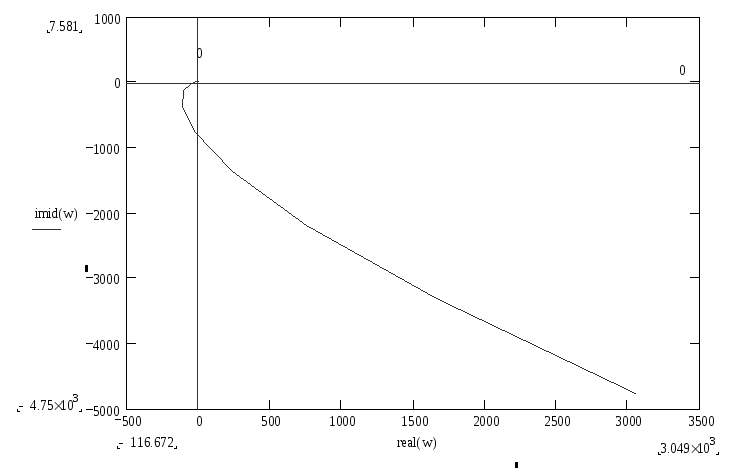исунок 1, б

Рисунок 1, в

Последний график показывает, что условие K=π/2*n, где K-угол поворота годографа, n-порядок характеристического уравнения, соблюдено. График уходит в бесконечность в 4 квадранте, система устойчива.

4.5 Критерий Найквиста

Требуется представить передаточную функцию в комплексной форме.

Соберем коэффициенты и выделим реальную и мнимую части.

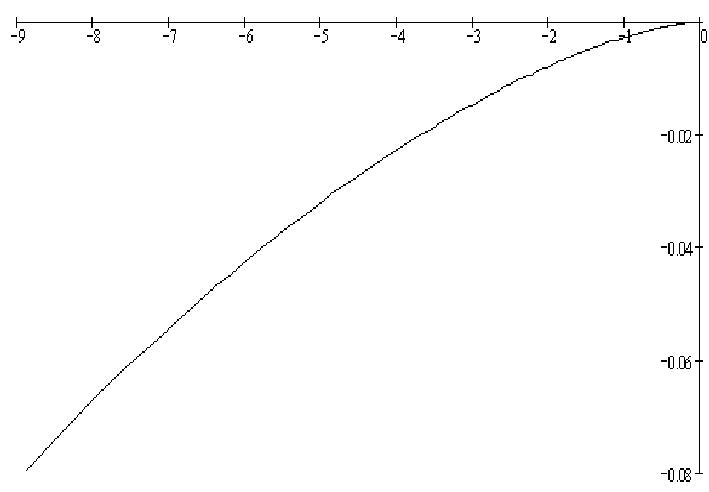
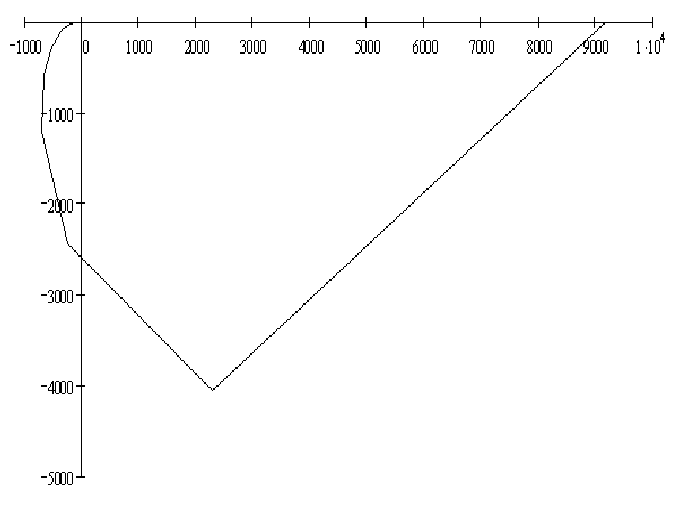
а) б)

Рисунок 2

Согласно критерию Найквиста система устойчива, т.к. график не охватывает (-1; 0) и заканчивается на положительной полуоси.

4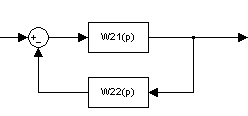.6 D-разбиение

Схема 8

Введем ООС с коэффициентом передачи W₂₂(p)=1 и примем W₉(p)=k , тогда

Характеристическое уравнение примет вид:

Используем замену p=jω, тогда:

В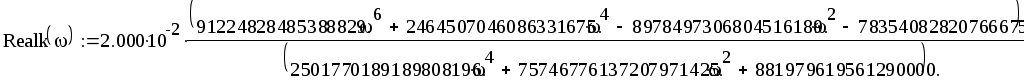ыделим реальную и мнимую части:

Re(k(ω))=

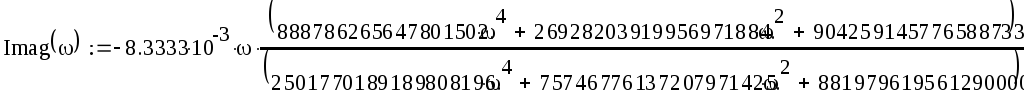
Im(k(ω))=

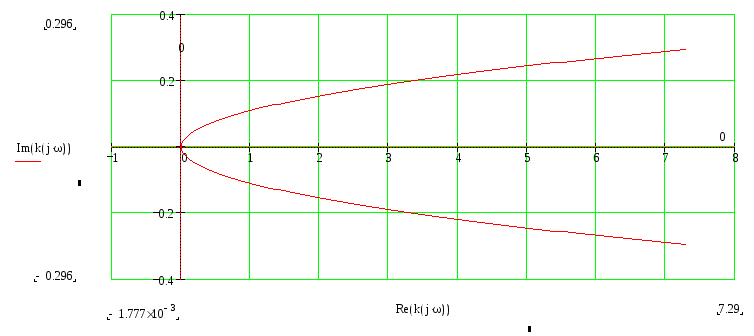
Рисунок 3

Согласно графику область k>-1.09E-4, является областью подозрительной на устойчивость. Определим правильность предположения с помощью критерия Гурвица. Примем k=5, то характеристическое уравнение запишется в виде:

=1.009E+12

(6.6918393)= 6.6918393

=1.345E+4

=3.579E+8

Т.о. система устойчива в области k>-1.09E-4

4.7 Критерий Ляпунова

Для того чтобы САУ была устойчива необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательные вещественные части.

Из передаточной функции замкнутой системы определим характеристическое уравнение.

Ниже приведено решение характеристического уравнения при помощи MathCAD.

Как видно, все корни отрицательные, т.е. система устойчива.

ВЫВОД

В ходе расчетно-графической работы мне была предоставлена СУ, имеющая некоторые недоработки. Я смог исправить недостатки и получить устойчивую систему, последнее было доказано с использованием семи критериев. Однако стоит отметить два критерия, которые являются наиболее простыми в своих классах: критерий Гурвица и Михайлова. Как показало построение АФЧХ, запас устойчивости не велик. Однако учитывая состав звеньев в системе (преобладание апериодических звеньев), данная ситуация трудно исправима и требует введение дополнительных звеньев, что не предусмотрено данной расчетной работой. Стоит отметить, что цель работы, получить устойчивую систему и проверить ее устойчивость, выполнена.

13