РГР / Решение2

1. Описание работы системы автоматического управления

   1. Принципиальная схема

Цель системы заключается в автоматическом слежении за положением самолеты или какого-либо иного объекта. На рис.1. электронный блок приемника вычисляет ошибку ε(t) между угловым положением объекта 𝛂₀(t) и направлением антенны 𝛂(t).

Рис. 1. Система радиолокационного сопровождения. Принципиальная схема

2. Функциональная схема

Рис. 2. Система радиолокационного сопровождения. Функциональная схема

Объектом управления является радар.

3. Структурная схема

Даны следующие значения передаточных функций:

W_Ус(P) =

W_Дв(P) =

Рис. 3. Система радиолокационного сопровождения. Структурная схема

W_𝛂o(P) =

Таким образом, схема состоит из следующих типовых звеньев:

W₁(P) = - апериодическое устойчивое звено;

W₂(P) = 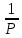– интегрирующее звено;

W₃(P) = = 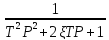если 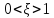, то звено колебательное устойчивое, иначе это два апериодических звена. Определим ξ:

,

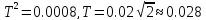
следовательно, можно разложить на 2 апериодических звена:

W₃(P) = (*)

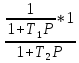Для вычисления коэффициентов T₁, T₂ необходимо решить следующее квадратное уравнение:

0,0008P² + 0.8P + 1 = 0 / (:0.0008)

P² + 1000 + 1250 = 0 (**)

D = b² - 4ac = 10⁶ - 4*1250 = 995000 > 0, √D = ±997.5

P_1,2 =

P₁ =

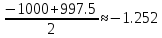
P₂ =

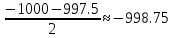
Уравнение (**) раскладывается на произведение сумм:

(P – P₁)(P – P₂) = 0

(P + 1.252)(P + 998.75) = 0

Необходимо произвести преобразование данного произведения к виду (*):

1.252 (1+0.799P) 998.75 (1 + 0.001P) = 0

Таким образом:

W₃(P) = , то есть получается два апериодических звена

W₃₁(P) = и W₃₂(P) =

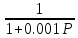
W₄(P) = 100 – усилительное звено.

2. Описание системы операторным и дифференциальным уравнениями

Структурные преобразования не требуются.

Передаточная функция для разомкнутой системы:

Рис. 4. Разомкнутая система

W_𝛂0(P) =

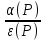
W_𝛂0(P) = W_Ус(P) W_Дв(P)

W_𝛂o(P) =

Передаточная функция для замкнутой системы:

Рис. 5. Замкнутая система

Ф_𝛂0(P) =

Ф_𝛂0(P) =

=

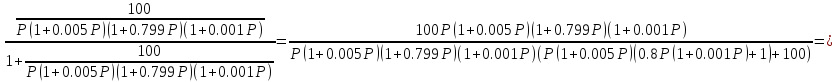
Характеристическое уравнение замкнутой системы, D(P):

D(P) = 0.000004P⁴ + 0.0048P³ + 0.805P² + P + 100

Операторное уравнение замкнутой системы:

(P) = Ф_𝛂0(P) 𝛂₀(P) + Ф_f(P) f(P), где f(P) – возмущающий сигнал, т.к. f(P) = 0, то получаем следующий вид операторного уравнения:

(P) = Ф_𝛂0(P) 𝛂₀(P)

(P) =

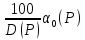
D(P) 𝛂(P) = 100 𝛂₀(P)

(0.000004P⁴ + 0.0048P³ + 0.805P² + P + 100) 𝛂(P) = 100 𝛂₀(P)

Производим обратную замену:

P=

Перейдем от операторного вида системы к дифференциальному:

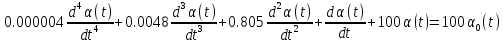
3. Оценка устойчивости САУ

Критерий устойчивости Рауса-Гурвица:

D(P) = 0.000004P⁴ + 0.0048P³ + 0.805P² + P + 100

a_i > 0, i = , следовательно, необходимое условие устойчивости выполняется

D(P) = 0

0.000004P⁴ + 0.0048P³ + 0.805P² + P + 100 = 0

Составляем матрицу Гурвица:

Δ₁ = a₁ = 0,0048 >0

Δ₂ = a₁ a₂ – a₃ a₀ = 0,0048*0,805 – 1*0,000004 = 0,00386 > 0

Δ₃ = a₃ Δ₂ – a₄ = a₃ Δ₂ - a₄ a₁² = 1*0,00386 – 100*0,0048² = 0,001556 > 0

Δ_i > 0, i=, следовательно, система устойчива.

Критерий устойчивости Найквиста:

W_𝛂0(P) =

W_𝛂0(P) =

Q(P) = P (1+0.005P) (1+0.799P) (1+0.001P)

Q(P) = 0, тогда

P (1+0.005P) (1+0.799P) (1+0.001P) = 0

Корни уравнения Q(P) = 0:

P₁ = 0

P₂ = -200

P₃ = -1.25

P₄ = -1000

Рис. 6. Корни уравнения Q(P)=0

Все корни принадлежат левой комплексной полуплоскости (R), следовательно, система устойчива в разомкнутом состоянии.

Построение АФЧХ в среде MatLab:

W_𝛂0(P) =

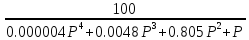
>> w=tf([100],[0.000004,0.0048,0.805,1,0])

>> nyquist(w)

Рис. 7. АФЧХ. Годограф Найквиста

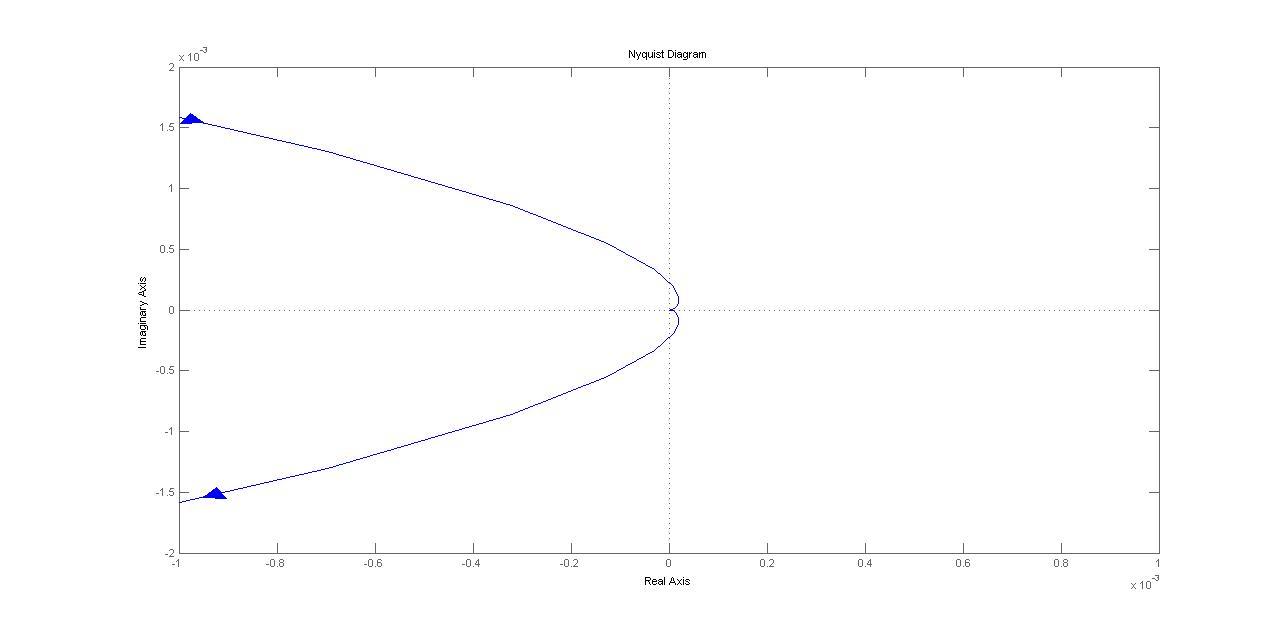
Рис. 8. АФЧХ. Годограф Найквиста. Увеличенный масштаб

Годограф Найквиста не охватывает особую точку (-1; j0), следовательно, система устойчивая.

Построение логарифмической АФЧХ

W₁(jω) = , где T=0.005, тогда ω_τ1=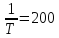, lg(ω_τ1) = 2.3 дек.

L₁(ω) = 20 lg

Ψ₁(ω) = arctg ( )

W₂(jω) = :

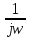L₂(ω) = -20 lg , где =1

Ψ₂(ω) =

W₃₁(jω) = , где T=0.799, тогда ω_τ31=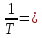1,252, lg(ω_τ31) = 0.097 дек.

L₃₁(ω) = 20 lg

Ψ₃₁(ω) = arctg ( )

W₃₂(jω) = , где T=0.001, тогда ω_τ32=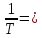1000, lg(ω_τ32) = 3 дек.

L₃₂(ω) = 20 lg

Ψ₃₂(ω) = arctg ( )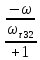

W₄(jω) = 100:

L₄(ω) = 20 lg100 = 20*2 = 40

Ψ₄(ω) = 0

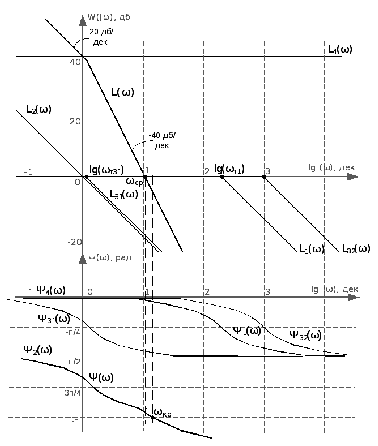
Рис. 9. Логарифмическая АФЧХ

По графику ЛАФЧХ видно, что ω_ср < ω_кр , следовательно, система устойчивая.

4. Построение модели исследуемой системы в среде MatLab

На вход исследуемой системы подается единичное воздействие. Выходной и входной сигналы снимаются с осциллографа

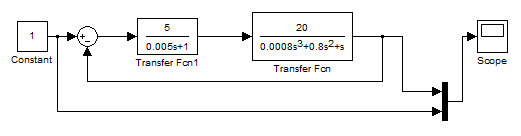
Рис. 10. Модель исследуемой системы в среде MatLab

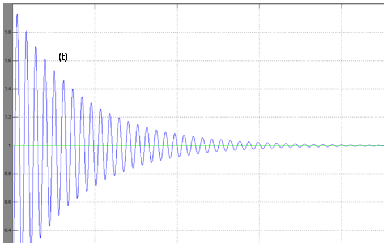
Рис. 11. Реакция исследуемой САУ на единичное воздействие

По переходной характеристике системы видно, что колебания затухают, значит, можно сделать вывод, что система устойчивая.

5. Синтез желаемой структуры САУ

Желаемая структура должна удовлетворять требованиям, заданным в ТЗ:

σ = 40%, тогда M = 1,58

ε_ст = 1,7%

t_пп = 1,75 сек

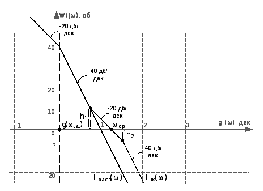
Рис. 12. ЛАФЧХ желаемой (L_ж(ω)) и располагаемой ((L_расп(ω)) структуры.

Область высоких частот мало влияет на характеристику системы, поэтому форма желаемой ЛАФЧХ может будет повторять форму располагаемой ЛАФЧХ. Область нижних частот определяется требованием к точности системы (ε_ст). Область средних частот определяется требованиями к запасу устойчивости и быстродействию системы.

Коэффициент добротности системы по скорости определяется следующим образом:

=

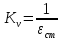
Определение границ области средних частот, M – колебательность системы:

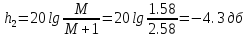
Для того, чтобы система удовлетворяла требованиям ТЗ, в её структуру последовательно включается корректирующее устройство.

Рис. 13. Структурная схема САУ с КУ

ЛАФЧХ последовательного корректирующего устройства получается вычитаем из L_ж(ω) L_расп(ω):

L_ку(ω) = L_ж(ω) - L_расп(ω)

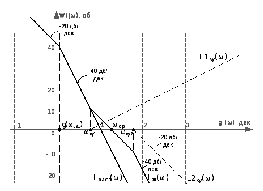
Рис. 14. ЛАФЧХ корректирующего звеньев устройства

, тогда 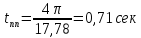. Данное значение удовлетворяет требованию ТЗ.

Из графика видно, что корректирующее устройство состоит из двух типовых звеньев:

– форсирующее звено первого порядка

- апериодическое устойчивое звено

Определение коэффициентов T₁, T₂:

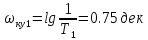, тогда T₁=0.18

, тогда T₂=0.018

Передаточная функция корректирующего устройства принимает следующий вид:

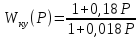, так как T₁>T₂ , то это реальное форсирующее звено.

Рис. 14. Структурная схема САУ с вычисленным КУ

6. Построение модели синтезированной системы в среде MatLab

Рис. 15. Модель синтезированной системы в среде MatLab

Рис. 16. Реакция синтезированной САУ на единичное воздействие

По графику определим коэффициент перерегулирования σ:

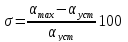, где 𝛂_max=1.233, 𝛂_уст=1, тогда .

Данное значение меньше заданного в ТЗ, значит, требование к запасу устойчивости выполняется.

Оценка точности синтезированной системы:

ε_уст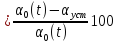 , где 𝛂₀(t) – входной сигнал, заданный константой, равный 1, 𝛂_уст = 1, тогда

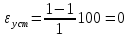. Это значение меньше заданного в ТЗ, следовательно, можно сделать вывод, что синтезированная система удовлетворяет требованию к точности.

Оценка быстродействия синтезированной системы:

t_пп 0,65 сек < 1.75 сек, следовательно, синтезированная система удовлетворяет требование к быстродействию.

Таким образом, синтезированная система удовлетворяем всем требованиям ТЗ.