РГР / ТАУ - Расчетная работа
.doc
Министерство
Образования Российской Федерации
Уфимский Государственный Авиационный Технический Университет
Кафедра ТК
Отчет по практической работе
по предмету «Основы теории управления»
Выполнил: студент
гр.Т28-320 ФИРТ
Проверила: Закиева Е.Ш.
Уфа, 2005
1. Задание на практику
Объектом исследования является следящая система, структурная схема которой представлена на рис. 1.
g(t)
Kред
s
Kизм
(t)
Iу
uд
Kу
L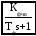
Рис. 1. Структурная схема следящей системы
Здесь: Кизм - передаточный коэффициент измерительного устройства;
Кфчв, Тф - коэффициент передачи и постоянная времени фазочувстви-тельного выпрямителя;
Ку коэффициент усиления электронного усилителя;
Кэму, Тэ - коэффициент передачи и постоянная времени электрома-шинного усилителя;
Кд, Тд - коэффициент передачи и постоянная времени электрического двигателя;
Кред - коэффициент передачи редуктора.
|
Кизм В/град |
Кэму В /мА |
Тфчв сек |
Тэму сек |
Кд |
Тд сек |
Кред |
Кфчв |
Задающие воздействие |
Допустимые ошибки |
||
|
|
|
ск град |
уск град |
||||||||
|
15 |
2,0 |
0,004 |
0,02 |
1 |
0,13 |
0,002 |
0,6 |
30 |
5 |
0,14 |
0,07 |
2. Выполнение
-
Исследовать устойчивость замкнутой системы с помощью критерия Гурвица. Приняв коэффициент усиления электронного усилителя Ку=100.
Передаточная функция разомкнутой системы:
Характеристический полином:
Матрица коэффициентов:
=
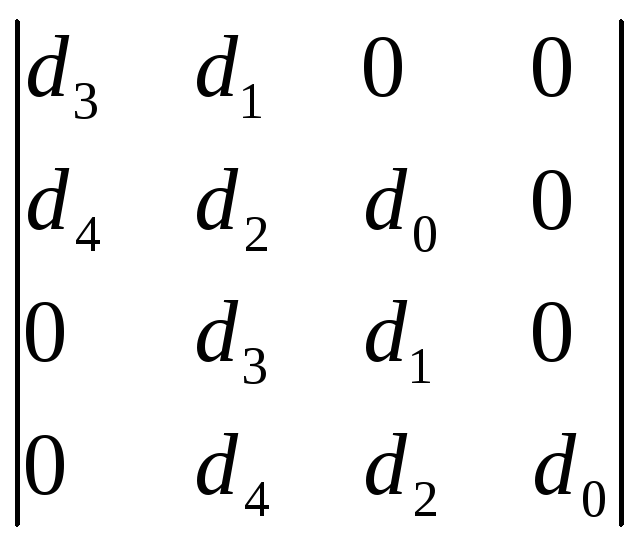Все
определители матрицы коэффициентов
положительны
система устойчива.
Определить критическое значение коэффициента усиления Ку, когда система находится на границе устойчивости.
Характеристический полином:
Матрица коэффициентов:
=
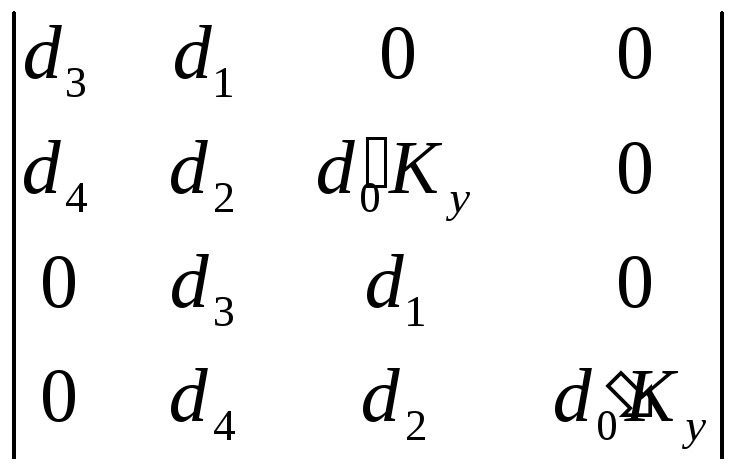входит
в определитель
.
Записываем определитель
и
приравниваем его к нулю, чтобы найти
критическое значение
.
– критическое
значение
,
при котором система будет находиться
на границе устойчивости.
-
Исследовать устойчивость замкнутой системы с помощью критерия Рауса.
Характеристический полином:
-
1
2
3
-
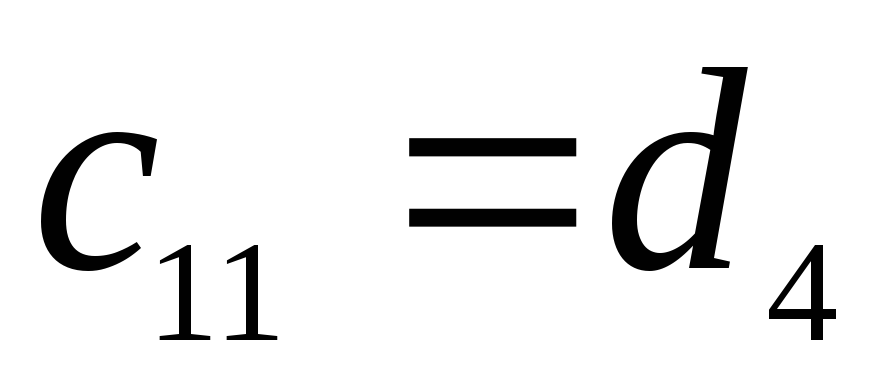
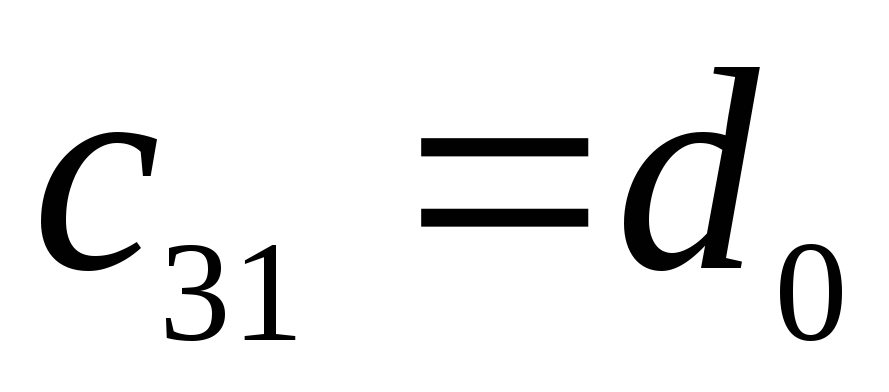
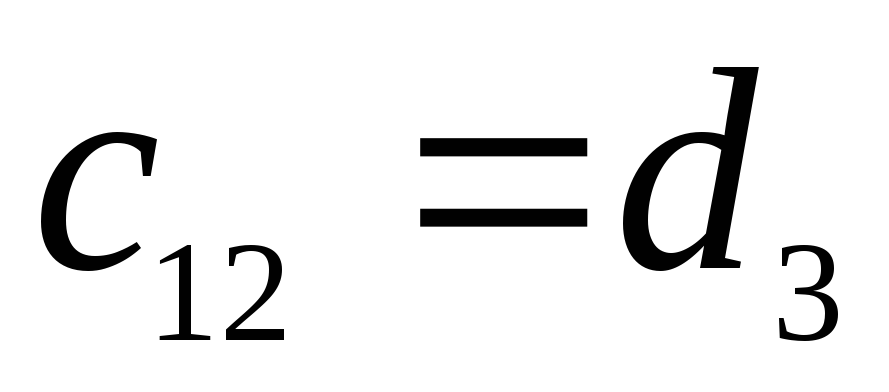
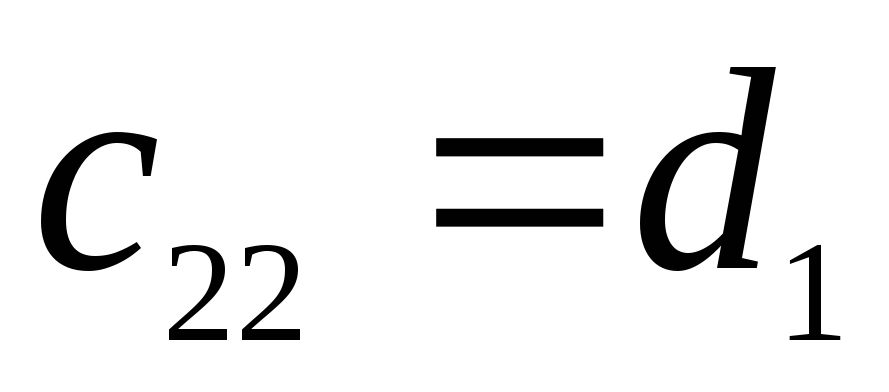
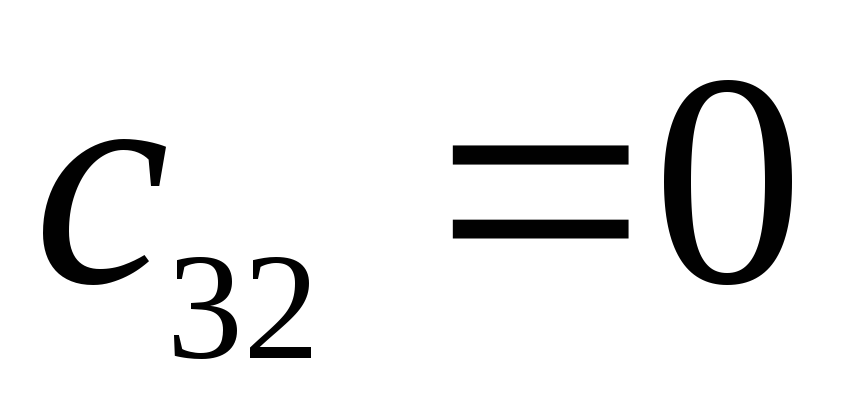
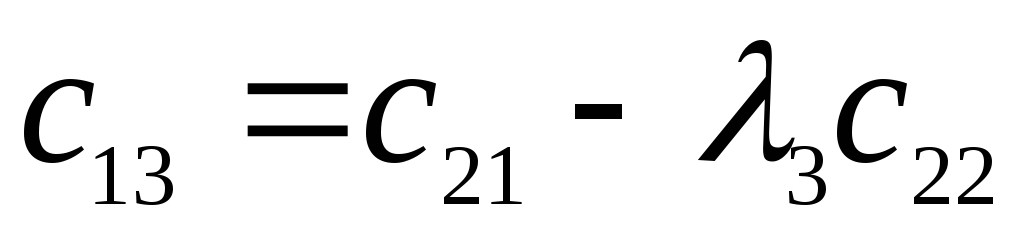
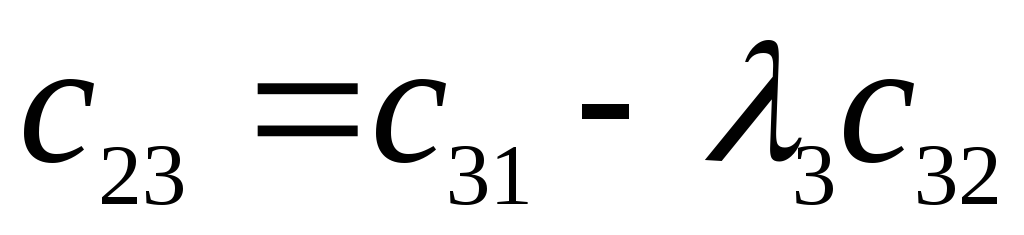
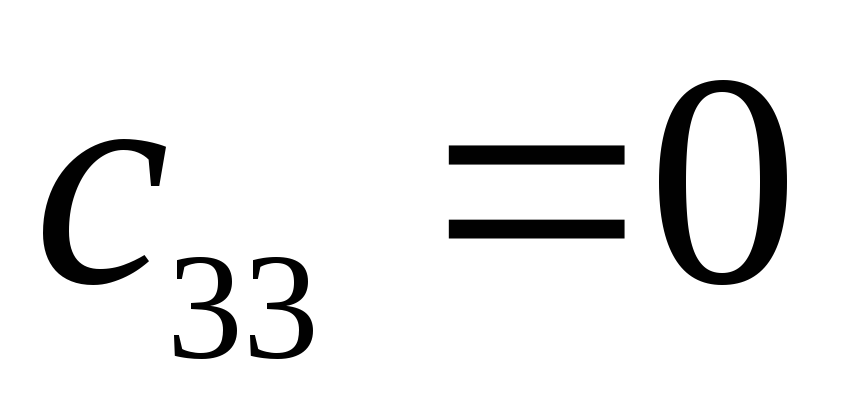
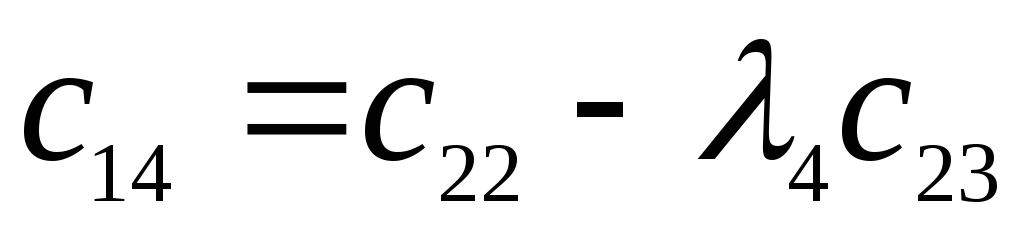
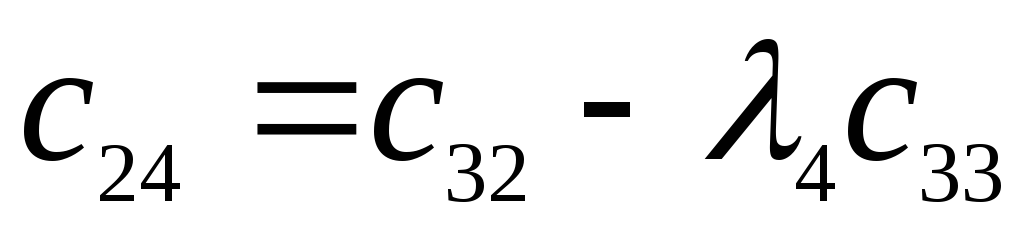
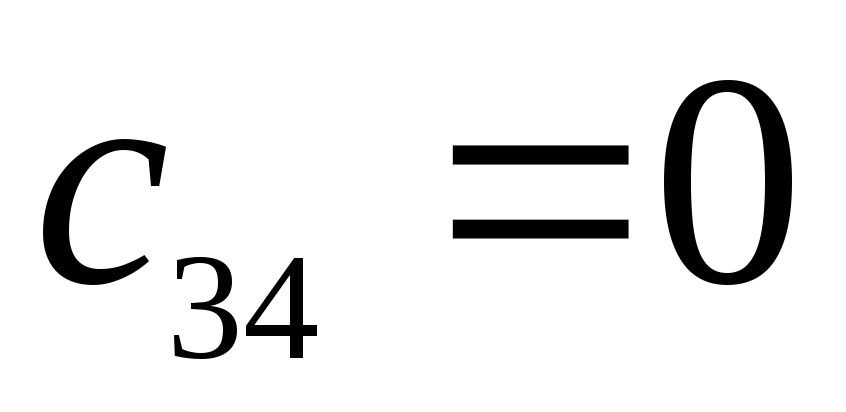
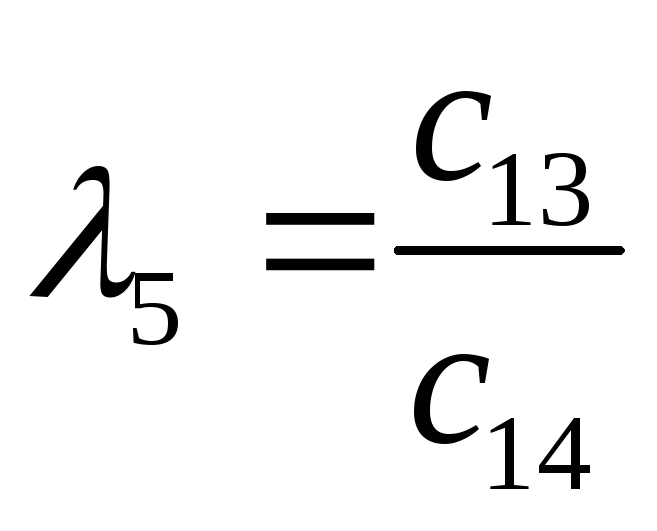
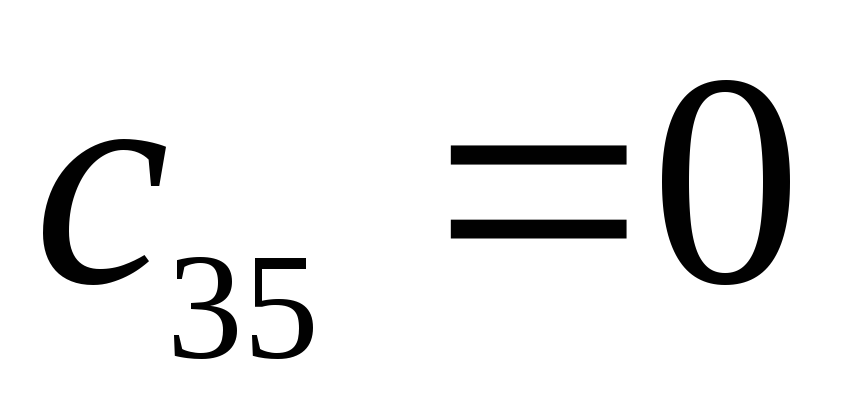
1
2
3
0.0000104
0.154
3.6
0.0032
1
0
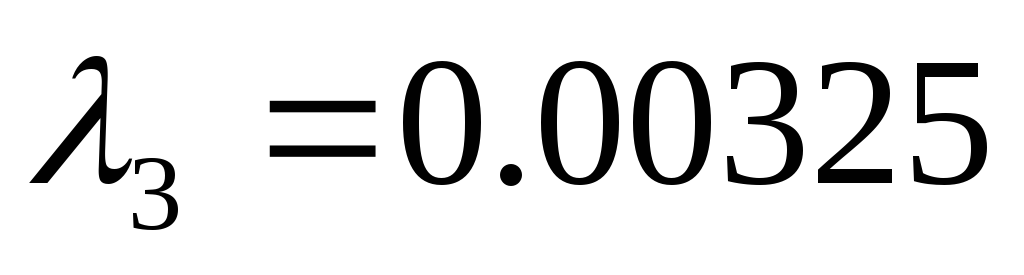
0.15075
3.6
0
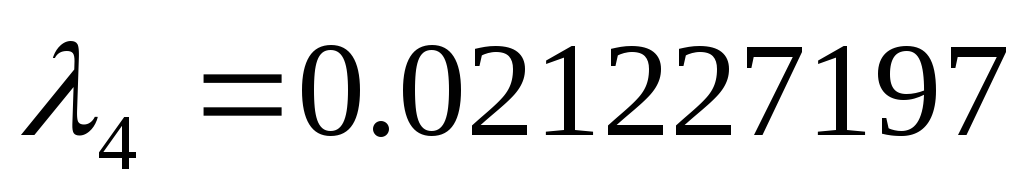
0.9235821
0
0
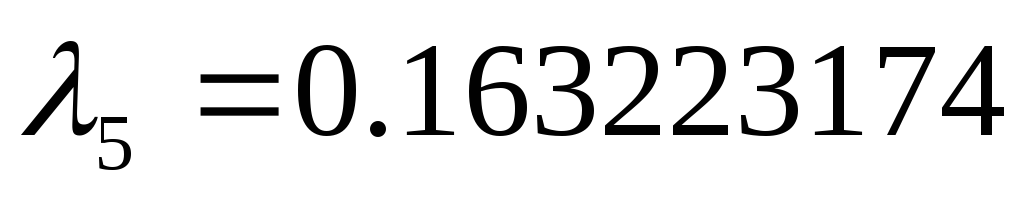
3.6
0
0
Коэффициенты
1-го столбца таблицы Рауса положительны
система устойчива.
-
Исследовать устойчивость замкнутой системы с помощью критерия Михайлова.
Характеристический полином:
Выделяем действительную и мнимую части:
Таблица
-
0
4.83876
17.677669
121.59062
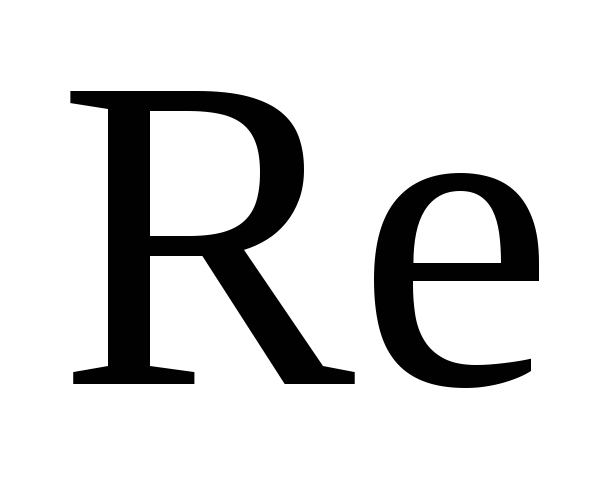
3.6
0
−43.5094
0
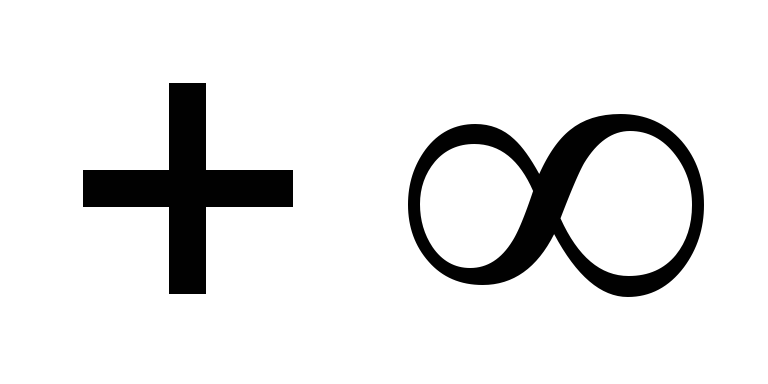
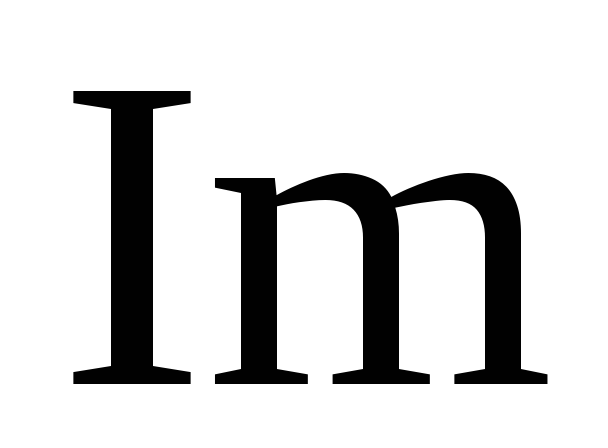
0
4.47623
0
−5630.824
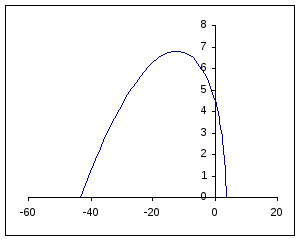
Критерий Михайлова:
САУ
устойчива, если годограф
начинается на действительной оси и с
ростом
от 0 до
обходит последовательно в положительном
направлении, то есть против часовой
стрелки
квадрантов, где
–
степень характеристи-ческого уравнения.
|
Для I,II квадрантов |
Для III,IV квадрантов |
|
|
|
Исследуемая система устойчива, т.к. годограф последовательно обходит 4 квадранта.
-
Исследовать устойчивость замкнутой системы с помощью критерия Найквиста.
Передаточная функция разомкнутой системы:
(АФХ)
АЧХ:
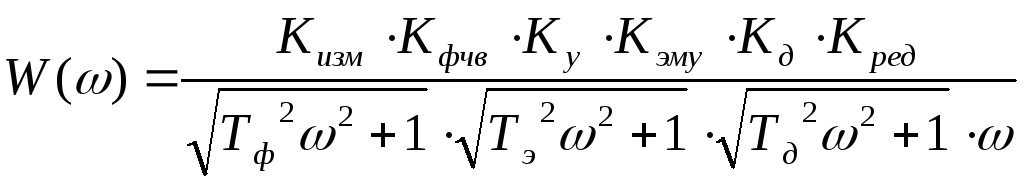
ФЧХ:
-
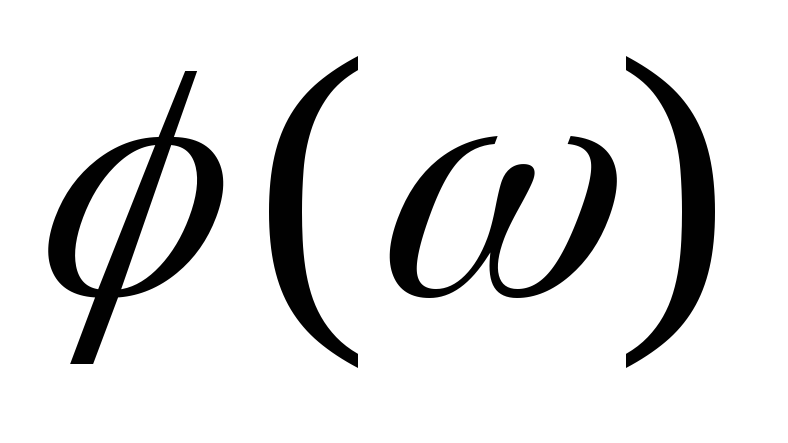
10
0,2150614
-2,7232713
-0,1965171
-0,0873638
20
0,0598036
-3,2347552
-0,0595443
0,0055634
30
0,0253756
-3,5504384
-0,0232841
0,0100881
40
0,0131052
-3,7850006
-0,0104849
0,0078621
50
0,0075912
-3,9717370
-0,0051223
0,0056025
60
0,0047496
-4,1256861
-0,0026295
0,0039554
70
0,0031443
-4,2556972
-0,0013866
0,0028220
80
0,0021741
-4,3676335
-0,0007348
0,0020462
90
0,0015565
-4,4655832
-0,0003803
0,0015093
100
0,0011465
-4,5524759
-0,0001826
0,0011318
110
0,0008647
-4,6304519
-0,0000708
0,0008618
120
0,0006654
-4,7011029
-0,0000075
0,0006654
130
0,0005210
-4,7656318
0,0000277
0,0005202
140
0,0004140
-4,8249635
0,0000465
0,0004114
150
0,0003333
-4,8798208
0,0000555
0,0003286
160
0,0002714
-4,9307774
0,0000588
0,0002650
170
0,0002234
-4,9782962
0,0000587
0,0002155
180
0,0001855
-5,0227561
0,0000566
0,0001766
190
0,0001553
-5,0644720
0,0000536
0,0001458
200
0,0001310
-5,1037087
0,0000500
0,0001211
210
0,0001113
-5,1406920
0,0000462
0,0001012
220
0,0000951
-5,1756164
0,0000425
0,0000851
230
0,0000818
-5,2086515
0,0000389
0,0000719
240
0,0000707
-5,2399461
0,0000356
0,0000611
250
0,0000614
-5,2696321
0,0000325
0,0000521
260
0,0000536
-5,2978270
0,0000296
0,0000447
270
0,0000470
-5,3246366
0,0000270
0,0000384
280
0,0000413
-5,3501561
0,0000246
0,0000332
290
0,0000365
-5,3744720
0,0000224
0,0000288
300
0,0000324
-5,3976629
0,0000205
0,0000251
10
0,2150614
-2,7232713
-0,1965171
-0,0873638
20
0,0598036
-3,2347552
-0,0595443
0,0055634
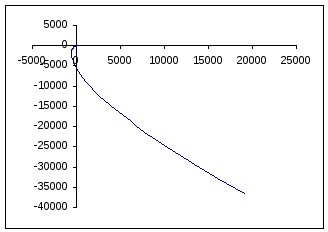
АФХ разомкнутой системы
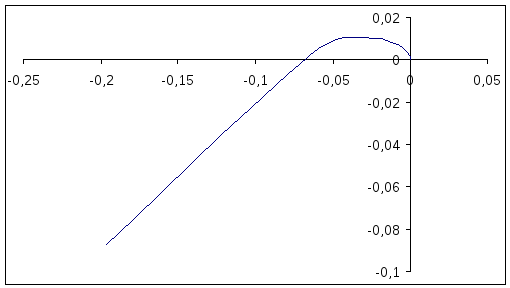
Критерий Найквиста:
САУ,
нейтральная в разомкнутом состоянии,
устойчива, если годограф разомкнутой
системы с его дополнением до бесконечности
не охватывает точку
.
Исследуемая
система устойчива, т.к. годограф не
охватывает точку
.
-
Исследовать устойчивость замкнутой системы с помощью логарифми-ческих частотных характеристик, оценить запасы устойчивости по фазе и амплитуде.
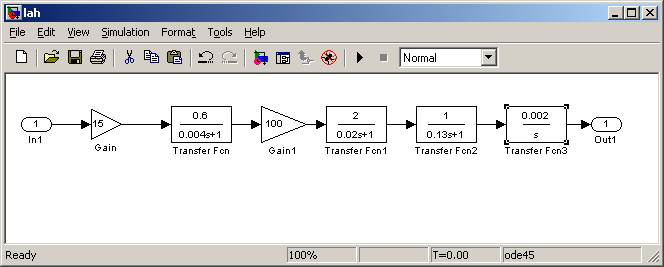
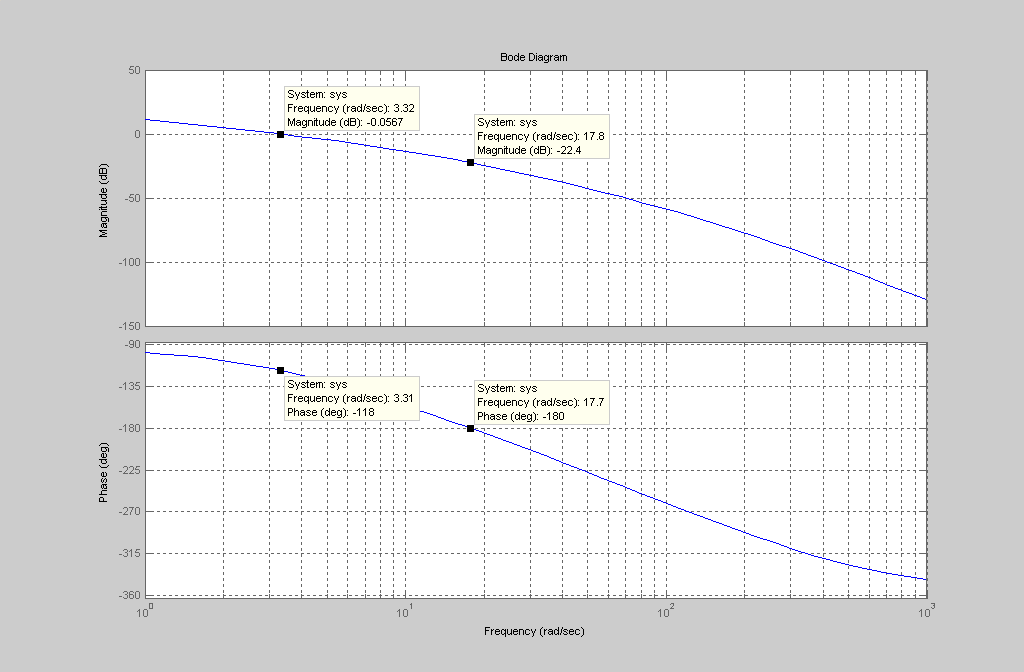
Запас
устойчивости по фазе:
Запас
устойчивости по модулю
:
-
Построить кривую D-разбиения по параметру Ку.
Характеристический полином:
Выделяем действительную и мнимую части:
Построим вспомогательные графики
и
-
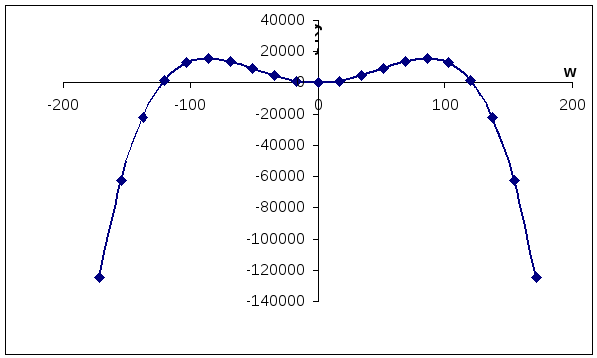
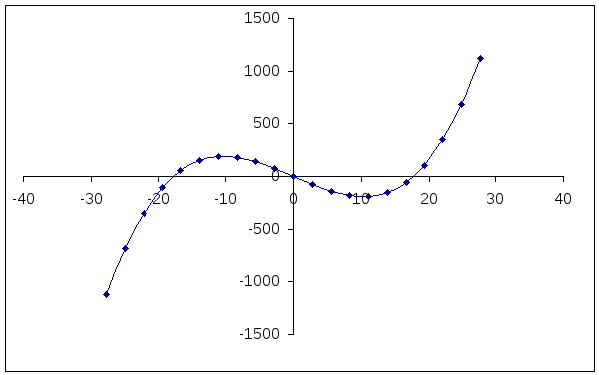
0
17.67767
86.04560508
121.6869
0
1308.594
15836.004274
0
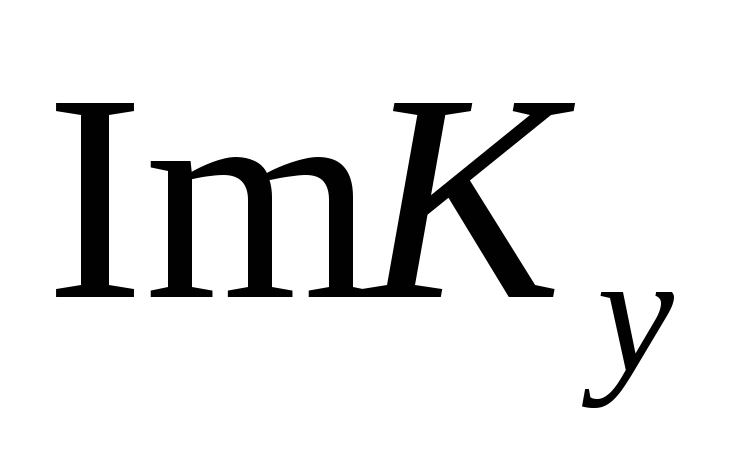
0
0
54238.1485
156788.8
