Де n2. Молекулярная (статистическая) физика и термодинамика.

7. Средняя энергия молекул

Средняя кинетическая энергия молекул газа при температуре  зависит от их конфигурации и структуры, что связано с возможностью различных видов движения атомов в молекуле и самой молекулы. При условии, что имеет место поступательное, вращательное движение молекулы как целого и колебательное движение атомов в молекуле, средняя кинетическая энергия молекулы кислорода () равна …

Решение: Для статистической системы в состоянии термодинамического равновесия на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная , а на каждую колебательную степень –  Средняя кинетическая энергия молекулы равна: .  Здесь – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы: , где  – число степеней свободы поступательного движения, равное 3;  – число степеней свободы вращательного движения, которое может быть равно 0, 2, 3;  – число степеней свободы колебательного движения, минимальное количество которых равно 1. Для молекулярного кислорода (двухатомной молекулы) ,  и . Следовательно, . Тогда средняя энергия молекулы кислорода () равна: .

Если не учитывать колебательные движения в молекуле водорода при температуре 200 К, то кинетическая энергия в (Дж) всех молекул в 4 г водорода равна …

Решение: Средняя кинетическая энергия одной молекулы равна: , где  – постоянная Больцмана, – термодинамическая температура;  – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы . Молекула водорода  имеет 3 поступательные и 2 вращательные степени свободы, следовательно,  В 4 г водорода содержится  молекул, где масса газа, молярная масса водорода, число Авогадро. Кинетическая энергия всех молекул будет равна:

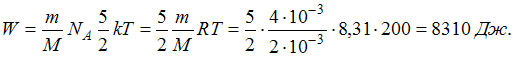
Если не учитывать колебательные движения в молекуле углекислого газа, то средняя кинетическая энергия молекулы равна …

Решение: Средняя кинетическая энергия молекулы равна: , где  – постоянная Больцмана, – термодинамическая температура;  – сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы: . Для молекулы углекислого газа  число степеней свободы поступательного движения , вращательного – , колебательного – , поэтому Следовательно, средняя кинетическая энергия молекулы  равна: .

1. Кинетическая энергия всех молекул в 2 г неона при температуре 300 К в  равна …

Решение: Средняя кинетическая энергия одной молекулы равна , где  – постоянная Больцмана, – термодинамическая температура,  – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы . Молекула неона имеет 3 поступательные степени свободы, следовательно, . В 2 г неона содержится  молекул, где масса газа, молярная масса неона, число Авогадро. Кинетическая энергия всех молекул будет равна: .

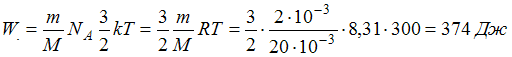2. При комнатной температуре отношение молярных теплоемкостей при постоянном давлении и постоянном объеме  равно  для газа …

гелия

водяного пара

воздуха

кислорода

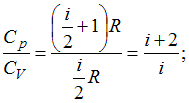
Решение: Из отношения   найдем , . Только 3 поступательные степени свободы имеют одноатомные газы, следовательно, это газ гелий.

3. В соответствии с законом равномерного распределения энергии по степеням свободы средняя кинетическая энергия молекулы идеального газа при температуре T равна: . Здесь , где ,  и  – число степеней свободы поступательного, вращательного и колебательного движений молекулы соответственно. Для гелия () число i равно …

3

5

7

6

Решение: Для статистической системы в состоянии термодинамического равновесия на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная , а на каждую колебательную степень – . Средняя кинетическая энергия молекулы равна: .  Здесь – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы: , где  – число степеней свободы поступательного движения, равное 3;  – число степеней свободы вращательного движения, которое может быть равно 0, 2, 3;  – число степеней свободы колебательного движения, минимальное количество которых равно 1. Для гелия () (одноатомной молекулы) ,  и . Следовательно, .