4. Работа. Энергия

14. МЕХАНИКА

1. Частица движется в двумерном поле, причем ее потенциальная энергия задается функцией . Работа сил поля по перемещению частицы из точки С (1, 1, 1) в точку В (2, 2, 2) равна … (Ответ введите в Дж. Учтите, что функция  и координаты точек заданы в единицах СИ.

Решение: Работа потенциальной силой совершается за счет убыли потенциальной энергии частицы: . Тогда

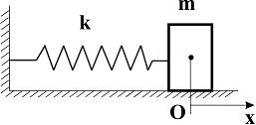
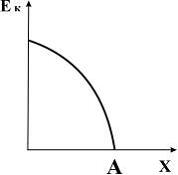
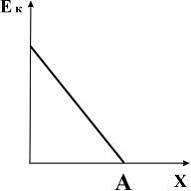
15. Тело массы m, прикрепленное к пружине с жесткостью k, может без трения   двигаться по горизонтальной поверхности (пружинный маятник). График зависимости кинетической энергии тела от величины его смещения из положения равновесия имеет вид, показанный на рисунке …

1)

2)

3)

Решение: По условию задачи трение отсутствует. Следовательно, в системе выполняется закон сохранения механической энергии: 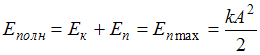, где А – амплитуда колебаний. Отсюда 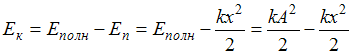. Здесь смещение х изменяется от 0 до А. Поэтому график зависимости кинетической энергии тела от величины его смещения из положения равновесия имеет вид 1).

16. Частица совершила перемещение по некоторой траектории из точки 1 с радиус-вектором  в точку 2 с радиус-вектором . При этом на нее действовала сила  (,  и  заданы в единицах СИ). Работа, совершенная силой , равна …

Решение: По определению . С учетом того, что ,  Дж.

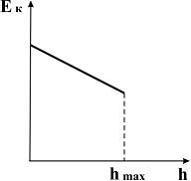
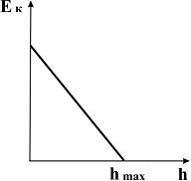
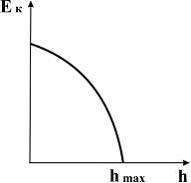
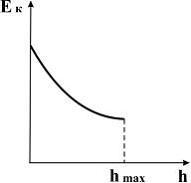
17. График зависимости кинетической энергии от высоты подъема тела, брошенного с поверхности земли под некоторым углом к горизонту, имеет вид, показанный на рис.

1

2

3

4

Решение: Из закона сохранения механической энергии 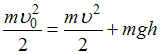 . Отсюда 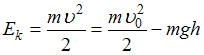, то есть зависимость  – линейная, причем, если h =0, 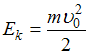; если же , 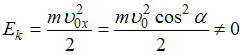. Поэтому график зависимости кинетической энергии от высоты подъема тела, брошенного с поверхности земли под некоторым углом к горизонту, имеет вид 1

18. Потенциальная энергия частицы задается функцией . -компонента (в Н) вектора силы, действующей на частицу в точке А (1, 2, 3) равна … (Учтите, что координаты точки А и функция  заданы в единицах СИ.)

Решение: Связь между потенциальной энергией частицы и соответствующей ей потенциальной силой имеет вид: , или , , 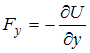. Таким образом, Н.

19. Тело массы  бросили с поверхности земли с начальной скоростью  под углом  к горизонту. Если пренебречь сопротивлением воздуха, средняя мощность, развиваемая силой тяжести за время падения тела на землю, равна

Решение: Средняя мощность, развиваемая силой за некоторый промежуток времени, равна отношению работы, совершаемой силой за рассматриваемый промежуток времени, к длительности этого промежутка: . Работа силы тяжести  и  по условию задачи. Тогда 0 и, следовательно, средняя мощность, развиваемая силой тяжести за время падения тела на землю, равна нулю.

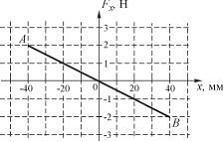
20. Шарик, прикрепленный к пружине и насаженный на горизонтальную направляющую, совершает гармонические колебания.

На графике представлена зависимость проекции силы упругости пружины на ось Х от координаты шарика. Работа силы упругости при смещении шарика из положения B в положение 0 в  составляет …

Решение: Работу силы упругости можно найти, определив площадь под графиком функции на участке ВО. 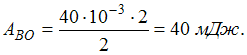 Работа положительна, так как шарик возвращается в положение равновесия.