
- •Контрольное тестирование по физике
- •Де n1. Механика.
- •1. Кинематика поступательного и вращательного движения
- •2. Динамика поступательного движения
- •3. Динамика вращательного движения
- •4. Работа. Энергия
- •5. Законы сохранения в механике
- •6. Элементы специальной теории относительности
- •Де n2. Молекулярная (статистическая) физика и термодинамика.
- •7. Средняя энергия молекул
- •8. Распределения Максвелла и Больцмана
- •9. Первое начало термодинамики. Работа при изопроцессах
- •10. Второе начало термодинамики. Энтропия
- •Де n3. Электричество и магнетизм.
- •11. Электростатическое поле в вакууме
- •12. Законы постоянного тока
- •13. Магнитостатика
- •14. Электрические и магнитные свойства вещества
- •15. Явление электромагнитной индукции
- •16. Уравнения Максвелла
- •Де n4. Механические и электромагнитные колебания и волны.
- •17. Свободные и вынужденные колебания
- •18. Сложение гармонических колебаний
- •19. Волны. Уравнение волны
- •20. Энергия волны. Перенос энергии волной
- •Де n5. Волновая и квантовая оптика.
- •21. Интерференция и дифракция света
- •22. Поляризация и дисперсия света
- •23. Эффект Комптона. Световое давление
- •24. Тепловое излучение. Фотоэффект
- •Де n6. Квантовая физика и физика атома.
- •25. Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
- •26. Спектр атома водорода. Правило отбора
- •27. Уравнение Шредингера (общие свойства)
- •28. Уравнение Шредингера (конкретные ситуации)
- •Де n7. Элементы ядерной физики и физики элементарных частиц.
- •29. Фундаментальные взаимодействия
- •30. Ядро. Элементарные частицы
- •31. Ядерные реакции.
- •32.Законы сохранения в ядерных реакциях
Де n6. Квантовая физика и физика атома.
25. Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
Ширина следа
электрона на фотографии, полученной с
использованием камеры Вильсона,
составляет
![]() Учитывая,
что постоянная Планка
Учитывая,
что постоянная Планка
![]() ,
а масса электрона
,
а масса электрона
![]() неопределенность
в определении скорости электрона будет
не менее …
неопределенность
в определении скорости электрона будет
не менее …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Из
соотношения неопределенностей Гейзенберга
для координаты и соответствующей
компоненты импульса
![]() следует,
что
следует,
что
![]() ,
где
,
где
![]() –
неопределенность координаты,
–
неопределенность координаты,
![]() –
неопределенность x-компоненты импульса,
–
неопределенность x-компоненты импульса,
![]() –
неопределенность x-компоненты скорости,
–
неопределенность x-компоненты скорости,
![]() –
масса частицы;
–
масса частицы;
![]() –
постоянная Планка, деленная на
–
постоянная Планка, деленная на
![]() .
Неопределенность x-компоненты скорости
электрона можно найти из соотношения
.
Неопределенность x-компоненты скорости
электрона можно найти из соотношения

Отношение длин волн де Бройля для молекул водорода и кислорода, соответствующих их наиболее вероятным скоростям при одной и той же температуре, равно …
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
Решение:
Длина
волны де Бройля определяется формулой где
где
![]() –
постоянная Планка,
–
постоянная Планка,
![]() и
и
![]() –
масса и скорость частицы. Наиболее
вероятная скорость молекулы
–
масса и скорость частицы. Наиболее
вероятная скорость молекулы
 Здесь
k
– постоянная Больцмана, R
– универсальная газовая постоянная,
Здесь
k
– постоянная Больцмана, R
– универсальная газовая постоянная,
![]() –
молярная масса газа. Тогда
–
молярная масса газа. Тогда
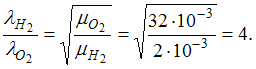
1. Если протон и дейтрон прошли одинаковую ускоряющую разность потенциалов, то отношение их длин волн де Бройля равно …
|
|
|
|
1 |
|
2 |
|
|
Решение: Дейтрон – ядро тяжелого
водорода (дейтерия). Длина волны де
Бройля определяется по формуле
 ,
где p – импульс частицы. Импульс
частицы можно выразить через ее
кинетическую энергию:
,
где p – импульс частицы. Импульс
частицы можно выразить через ее
кинетическую энергию:
 .
По теореме о кинетической энергии,
согласно которой работа сил электрического
поля идет на приращение кинетической
энергии,
.
По теореме о кинетической энергии,
согласно которой работа сил электрического
поля идет на приращение кинетической
энергии,
![]() .
Отсюда можно найти
.
Отсюда можно найти
![]() ,
полагая, что первоначально частица
покоилась:
,
полагая, что первоначально частица
покоилась:
![]() .
Окончательное выражение для длины
волны де Бройля через ускоряющую разность
потенциалов имеет вид:
.
Окончательное выражение для длины
волны де Бройля через ускоряющую разность
потенциалов имеет вид:
 .
Учитывая, что
.
Учитывая, что
![]() и
и
![]() ,
отношение длин волн де Бройля протона
и дейтрона равно:
,
отношение длин волн де Бройля протона
и дейтрона равно:

2. Отношение неопределенностей проекций скоростей нейтрона и α-частицы на некоторое направление при условии, что соответствующие координаты частиц определены с одинаковой точностью, равно …
|
|
4 |
|
|
|
2 |
|
|
Решение: Из соотношения неопределенностей
Гейзенберга для координаты и соответствующей
компоненты импульса
![]() следует,
что
следует,
что
![]() ,
где
,
где
![]() –
неопределенность координаты,
–
неопределенность координаты,
![]() –
неопределенность x-компоненты импульса,
–
неопределенность x-компоненты импульса,
![]() –
неопределенность x-компоненты скорости,
–
неопределенность x-компоненты скорости,
![]() –
масса частицы;
–
масса частицы;
![]() –
постоянная Планка, деленная на
–
постоянная Планка, деленная на
![]() .
Неопределенность x-компоненты скорости
можно найти из соотношения
.
Неопределенность x-компоненты скорости
можно найти из соотношения
![]() .
Поскольку
.
Поскольку
![]() для
обеих частиц одинаковы, искомое отношение
равно:
для
обеих частиц одинаковы, искомое отношение
равно:
 .
.
3. Высокая монохроматичность лазерного
излучения обусловлена относительно
большим временем жизни электронов в
метастабильном состоянии, равном
![]() .
Учитывая, что постоянная Планка
.
Учитывая, что постоянная Планка
![]() ,
ширина метастабильного уровня будет
не менее …
,
ширина метастабильного уровня будет
не менее …
|
|
0,66 пэВ |
|
66 пэВ |
|
1,52 ТэВ |
|
0,66 нэВ |
Решение: Соотношение неопределенностей
для энергии и времени имеет вид
![]() ,
где
,
где
![]() неопределенность
в задании энергии (ширина энергетического
уровня),
неопределенность
в задании энергии (ширина энергетического
уровня),
![]() время
жизни частицы в данном состоянии. Тогда
время
жизни частицы в данном состоянии. Тогда
 .
.
