13. Магнитостатика

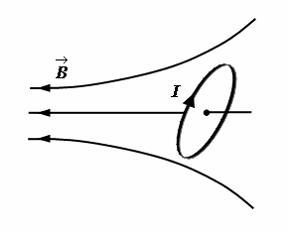
Небольшой контур с током I помещен в неоднородное магнитное поле с индукцией . Плоскость контура перпендикулярна плоскости чертежа, но не перпендикулярна линиям индукции. Под действием поля контур …

			повернется против часовой стрелки и сместится влево
			повернется против часовой стрелки и сместится вправо
			повернется по часовой стрелке и сместится вправо
			повернется по часовой стрелке и сместится влево

Решение: На контур с током в однородном магнитном поле действует вращающий момент , стремящийся расположить контур таким образом, чтобы вектор его магнитного момента  был сонаправлен с вектором магнитной индукции  поля. Если контур с током находится в неоднородном магнитном поле, то на него действует еще и результирующая сила, под действием которой незакрепленный контур втягивается в область более сильного поля, если угол между векторами  и  острый (α < 90°). Если же указанный угол тупой (α > 90°), то контур с током выталкивается в область более слабого поля, поворачивается под действием вращающего момента, так что угол становится острым, и затем втягивается в область более сильного поля. В соответствии с этим контур повернется против часовой стрелки и сместится влево.

10. Электрон влетает в магнитное поле, создаваемое прямолинейным длинным проводником с током в направлении, параллельном проводнику (рис.). При этом сила Лоренца, действующая на электрон,

	лежит в плоскости чертежа и направлена вправо
	лежит в плоскости чертежа и направлена влево
	перпендикулярна плоскости чертежа и направлена «от нас»
	перпендикулярна плоскости чертежа и направлена «к нам»

Решение: На заряженную частицу, движущуюся в магнитном поле, действует сила Лоренца. В данном случае магнитное поле создается прямолинейным длинным проводником с током I. В соответствии с правилом правого винта (буравчика) вектор магнитной индукции в месте расположения электрона направлен перпендикулярно плоскости чертежа «от нас». Поскольку скорость электрона перпендикулярна вектору магнитной индукции, для нахождения направления силы Лоренца удобно воспользоваться правилом левой руки. С учетом знака заряда двигающейся частицы сила Лоренца лежит в плоскости чертежа и направлена вправо.

11. Поле создано прямолинейным длинным проводником с током I1. Если отрезок проводника с током I2 расположен в одной плоскости с длинным проводником так, как показано на рисунке, то сила Ампера

	лежит в плоскости чертежа и направлена вправо
	лежит в плоскости чертежа и направлена влево
	перпендикулярна плоскости чертежа и направлена «от нас»
	перпендикулярна плоскости чертежа и направлена «к нам»

Решение: На проводник с током в магнитном поле действует сила Ампера. В данном случае магнитное поле создается прямолинейным длинным проводником с током I₁. В соответствии с правилом правого винта (буравчика) вектор магнитной индукции в месте расположения отрезка проводника с током I₂ направлен перпендикулярно плоскости чертежа «к нам». В случае прямолинейного отрезка проводника с током в перпендикулярном проводнику магнитном поле для нахождения направления силы Ампера удобно воспользоваться правилом левой руки, согласно которому сила Ампера лежит в плоскости чертежа и направлена вправо.

12. На рисунке показаны траектории заряженных частиц, с одинаковой скоростью влетающих в однородное магнитное поле, перпендикулярное плоскости рисунка. При этом для зарядов и удельных зарядов частиц верным является утверждение …

	, ,		, ,
	, ,		, ,

Решение: На заряженную частицу, двигающуюся в магнитном поле, действует сила Лоренца. В том случае, когда скорость частицы  перпендикулярна линиям магнитной индукции, направление силы Лоренца удобно находить по правилу левой руки. Тогда из рисунка следует, что , , , . В данном случае траектории заряженных частиц – дуги окружностей с различающимися радиусами. Поскольку радиус окружности обратно пропорционален удельному заряду частицы, , то из рисунка следует, что .

13. На рисунке изображены сечения двух прямолинейных длинных параллельных проводников с противоположно направленными токами, причем  . Индукция  магнитного поля равна нулю на участке … Решение: Линии магнитной индукции прямолинейных длинных проводников с токами  и  представляют собой концентрические окружности, плоскости которых перпендикулярны проводникам, а центры лежат на их осях. Направления этих линий определяют правилом правого винта: направление вращения винта дает направление силовой линии магнитной индукции, если поступательное движение винта совпадает с направлением тока в проводнике. Индукция  результирующего магнитного поля определяется по принципу суперпозиции  и равна нулю, если векторы  и  противоположно направлены и равны по модулю.  Это может быть только в точках интервалов а и d. Поскольку магнитная индукция прямолинейного длинного проводника с током вычисляется по формуле , то модули векторов  и равны, если , так как по условию . Следовательно, индукция  результирующего магнитного поля равна нулю в некоторой точке интервала а.