§ 2.3. Метод потенціалів розв’язування транспортної задачі
Перейдемо до опису методу розв’язування задачі (2.1.1) – (2.1.3). Вважатимемо, що початковий невироджений базисний план перевезень
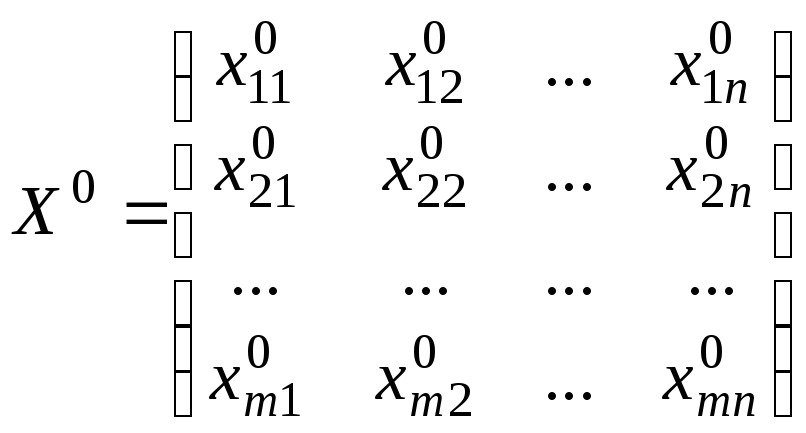
знайдено.
Серед компонент
є рівно
більших нуля. Побудуємо таблицю
-
...
...
...
...
...
...
...
...
...
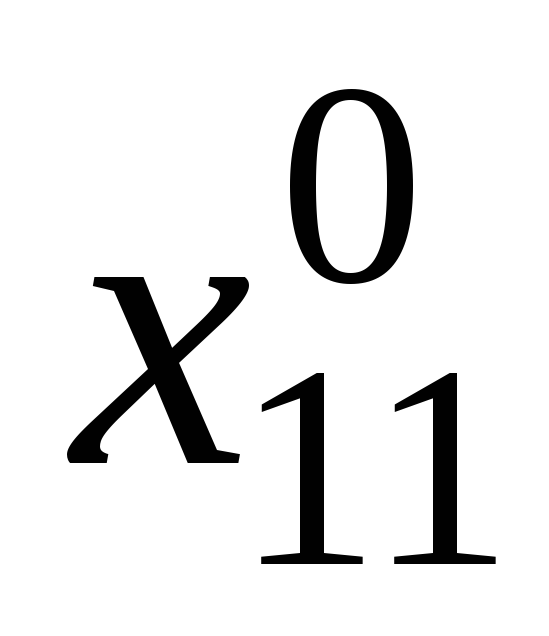
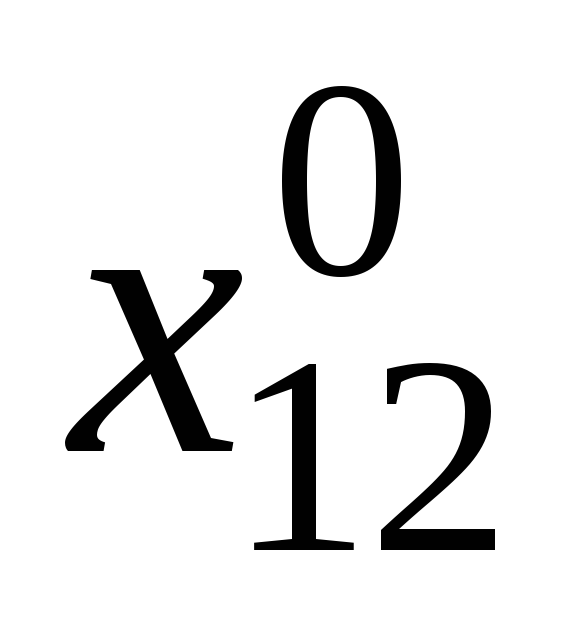
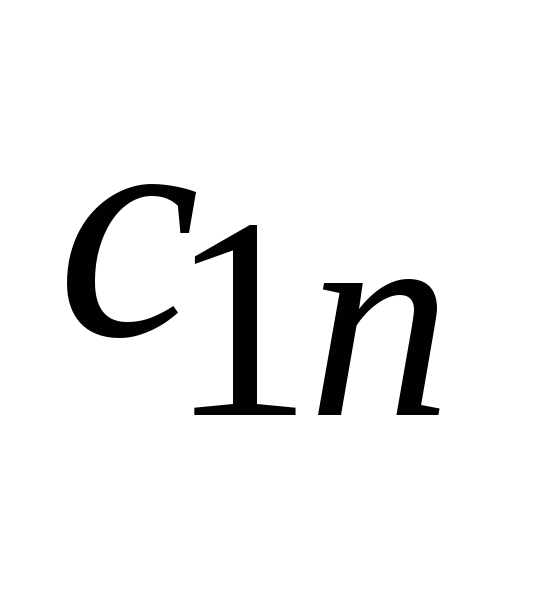
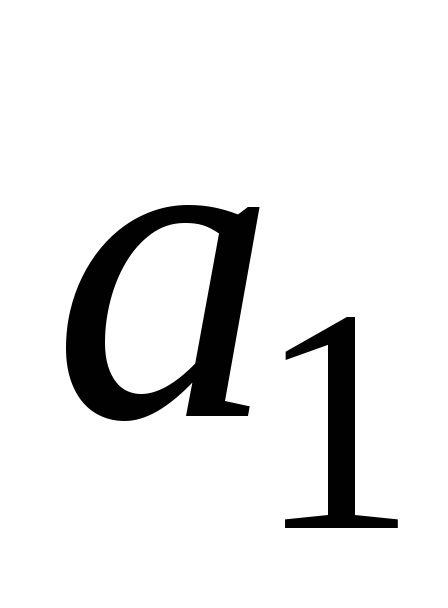
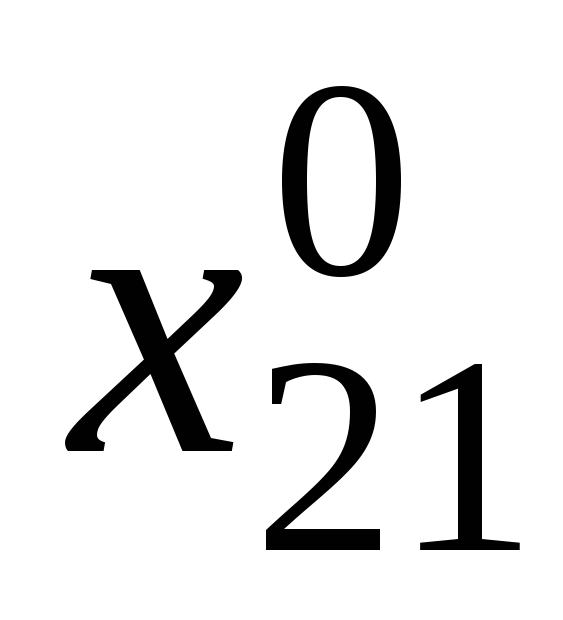
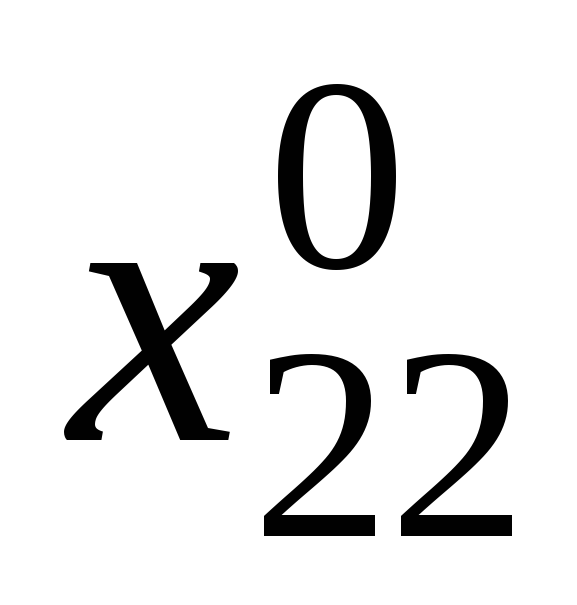
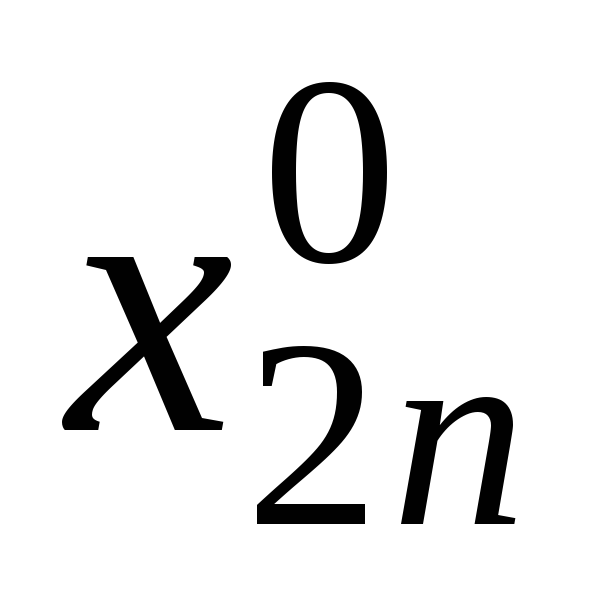
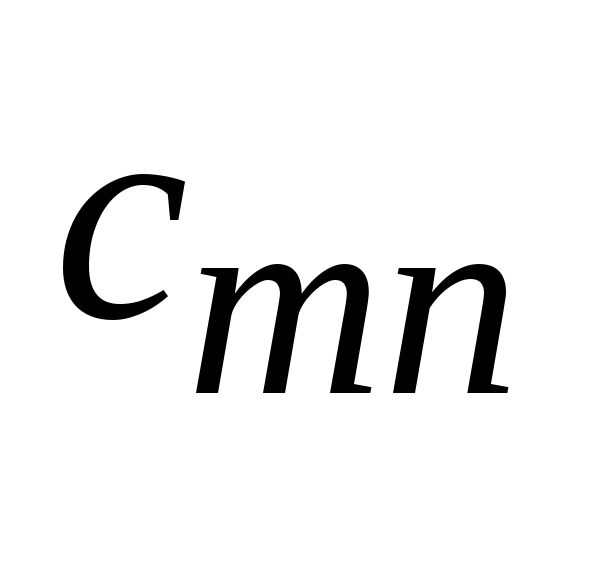
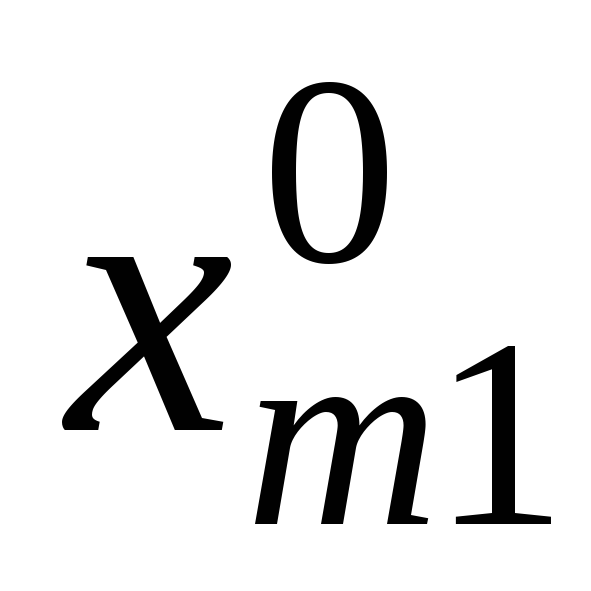
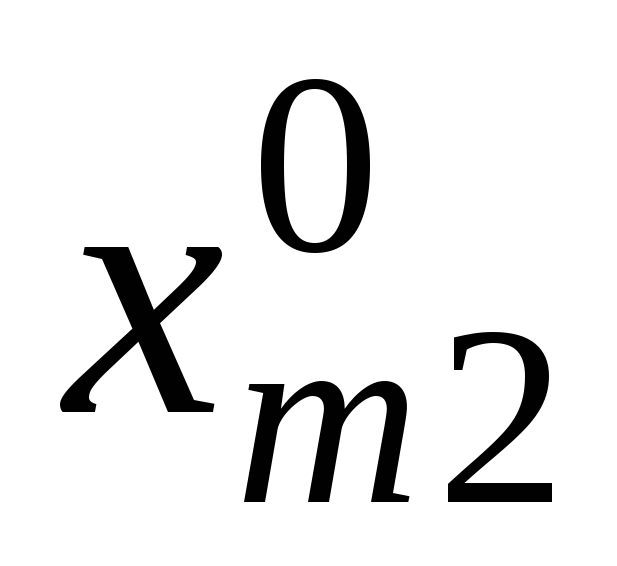
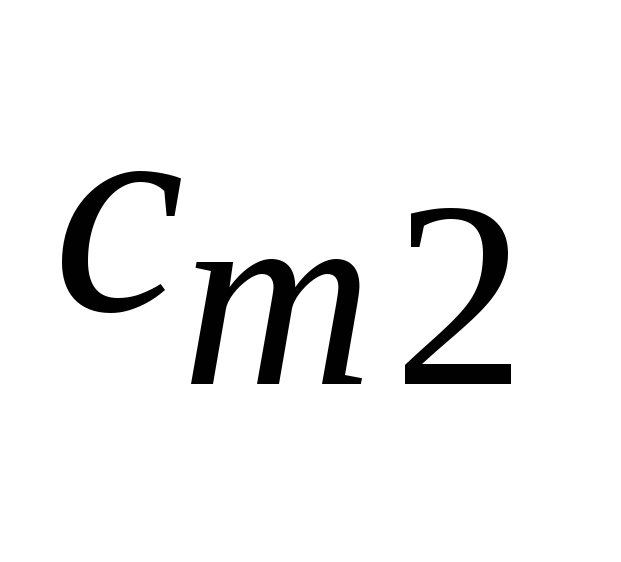
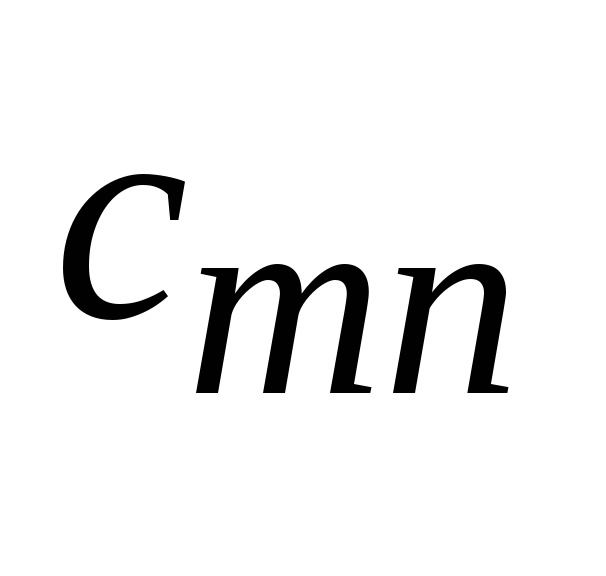
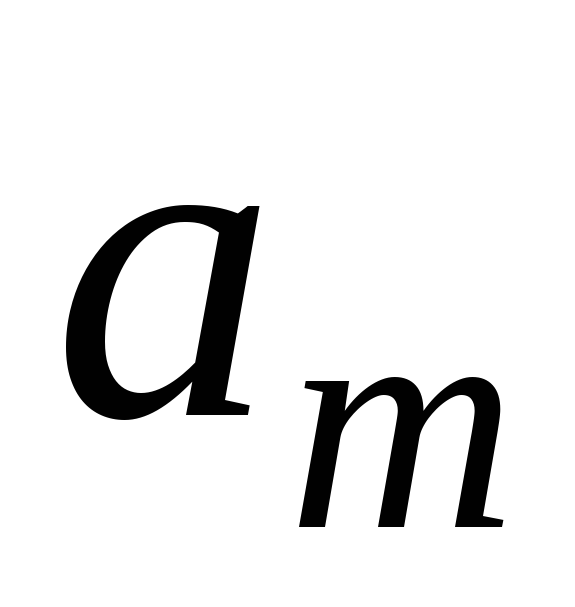
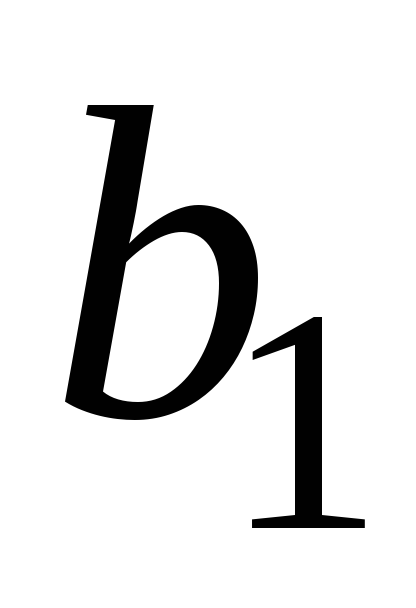
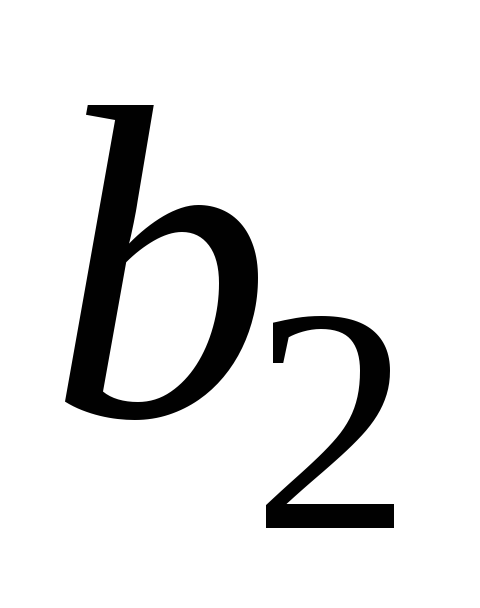
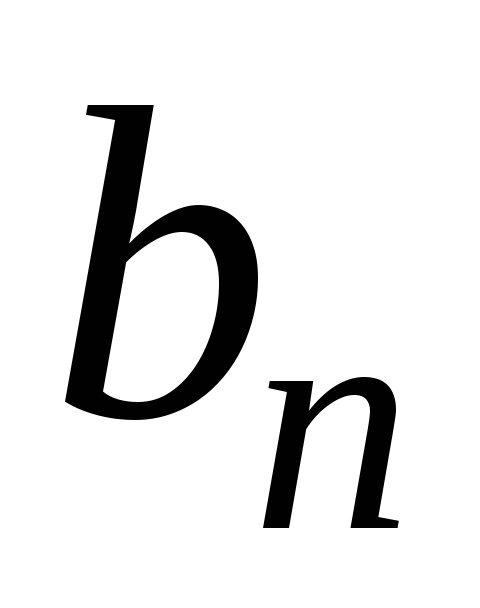
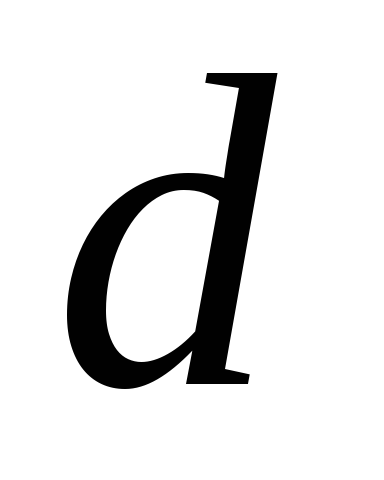
Як і
раніше,
.
У клітинку
таблиці вписано
(правий верхній кут) та компоненти
початкового плану (лівий нижній кут).
Теоретичною
основою запропонованого нижче методу
потенціалів
є друга теорема двоїстості в лінійному
програмуванні. Як уже зазначалося,
невироджений базисний план оптимальний,
якщо для цього існують такі потенціали
та
,
що задовольняють умови (2.1.7) і (2.1.8). Всякий
базисний невироджений план (у тому числі
)
можна перевірити на оптимальність,
використовуючи (2.1.7), (2.1.8). Для
ці умови є умовами існування
та
,
таких, що
,
якщо
, (2.3.1)
,
якщо
. (2.3.2)
Оскільки
у плані
рівно
компонент
,
більших нуля, то (2.3.1) є системою
рівнянь із
невідомими
та
.
Невідомих на одиницю більше, ніж рівнянь.
У зв’язку з базисністю плану
система (2.3.1) має розв’язок. Один із
таких розв’язків може бути легко
визначений, якщо припустити, наприклад,
що
(можна надати довільного фіксованого
значення будь-якому з невідомих
потенціалів, а інші визначити із системи
(2.3.1)).
Наприклад,
якщо розглянути початковий базисний
план
,
визначений методом північно-західного
кута в попередньому параграфі,
-
20
2
10
1
2
2
30
3
5
2
35
1
3
40
1
3
5
3
25
1
30
20
15
40
25
100
то система рівнянь (2.3.1) матиме вигляд
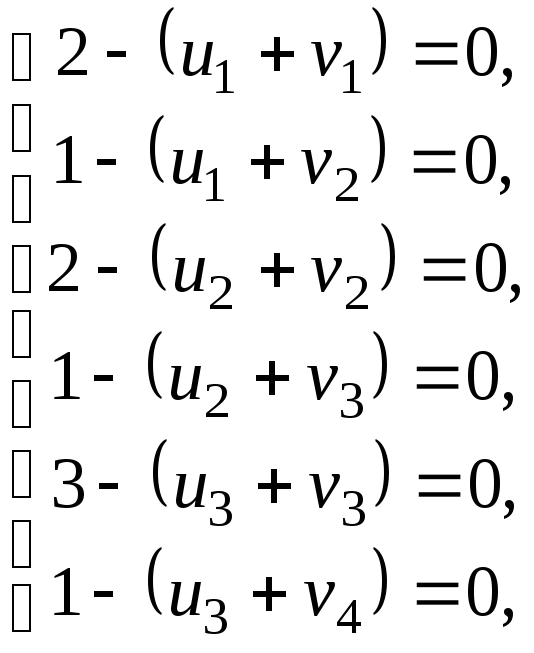
або
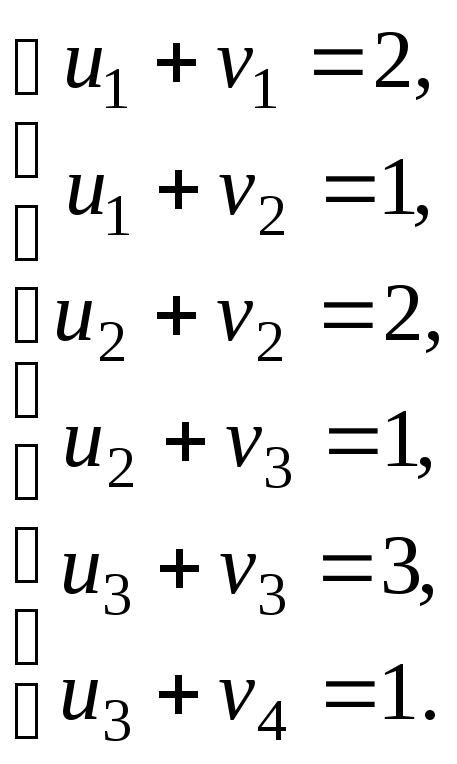
Вважатимемо,
що
,
легко визначаємо послідовно
,
,
,
,
,
.
Перевірка умов (2.3.2) дає
,
,
,
,
,
.
Ми
бачимо, що умови (2.3.2) не виконуються, бо
і
.
План не оптимальний. Що стосується цього
конкретного плану, то наперед було
відомо, що він і не міг бути оптимальним,
бо план, визначений за методом мінімального
елемента, як ми переконались раніше,
кращий
.
Нижче буде запропоновано метод, який дозволяє перейти до нового базисного плану
,
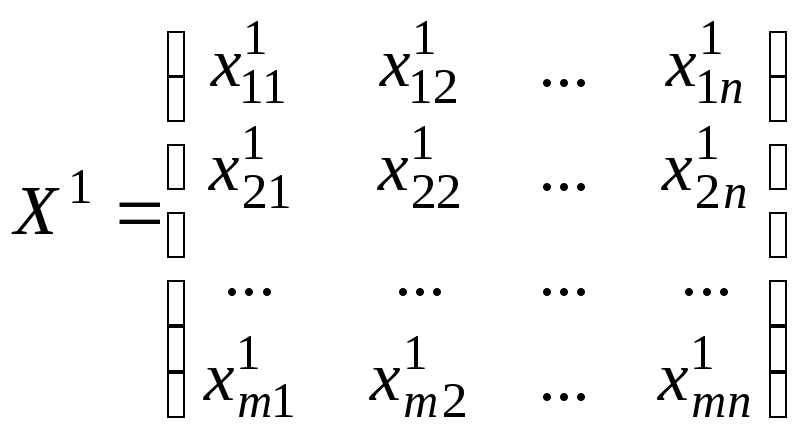причому значення цільової функції на цьому плані буде меншим.
Нехай,
наприклад, для плану
не виконуються умови (2.3.2), бо для деякої
клітинки
та деякої клітинки таблиці такої, що
,
справджується нерівність 
.
Побудуємо
в таблиці цикл, вершинами якого є клітинка
та деякі клітинки таблиці, відповідні
лише базисним змінним плану
(клітинки, в яких
).
Клітинку
таблиці позначимо ще знаком “+” чи “–”
так, щоб при обході циклу знаки чергувалися.
Визначимо найменше значення серед
компонент плану
,
які вписані в клітинки, позначені знаком
“–”. Позначимо отримане число символом
.
Перейдемо до нового плану
за правилом:
,
якщо клітинка
не є вершиною циклу;
,
якщо клітинка
є вершиною циклу і позначена в ньому
знаком “+”;
,
якщо клітинка
є вершиною циклу і позначена в ньому
знаком “–”.
Не важко
довести, що
є планом і що
,
тобто значення функції затрат зменшується
на число
.
Зважаючи
на це, серед клітинок таблиці, в яких не
виконується умова (2.3.2) як
бажано вибирати таку, для якої
найбільше. Але, щоб не будувати багато
циклів, дещо спрощують алгоритм і
вибирають як
клітинку, для якої
найбільше.
Проілюструємо сказане на прикладі, який розглядався вище.
Оскільки
,
позначаємо знаком “+” клітинку (3,1) і
будуємо цикл. Він зображений у таблиці.
При цьому
.
-
2
0–2
1
0+1
2
2
30
3
5
–2
3
5+1
3
40
+
1
3
5–
3
25
1
30
20
15
40
25
100
Здійснимо
перехід до нового плану
згідно зі сформульованим вище правилом
і отримаємо таблицю
-
15
2
15
1
2
2
30
3
2
40
1
3
40
5
1
3
3
25
1
30
20
15
40
25
100
Відповідне отриманому плану
значення функції затрат рівне
.
Це
значення на
менше за значення затрат на плані 
.
Розв’яжемо методом потенціалів два приклади.
Приклад 1. Розв’язати транспортну задачу
-
2
3
3
1
26
1
4
1
3
31
2
2
3
2
23
20
15
25
20
80
Тут у
клітинках таблиці (верхній правий кут)
уписані питомі затрати
на перевезення з пункту
в пункт
.
У правому стовпці вписано запаси в
пунктах
,
а в нижньому рядку – потреби пунктів
.
Легко перевірити, що, згідно із Твердженням 2.2.1, запропонована ТЗ невироджена.
Початковий
план
визначимо за методом північно-західного
кута, виписуючи
в лівому нижньому кутку клітинки.
Отримаємо
-
20
2
6
3
3
1
26
1
9
–4
2
2+1
3
31
2
+
2
3–
3
20
2
23
20
15
25
20
80
У нас
,
,
і отриманий базисний план перевезень
невироджений. Затрати на його реалізацію
дорівнюють
.
Вважаючи
,
обчислимо потенціали
із системи рівнянь
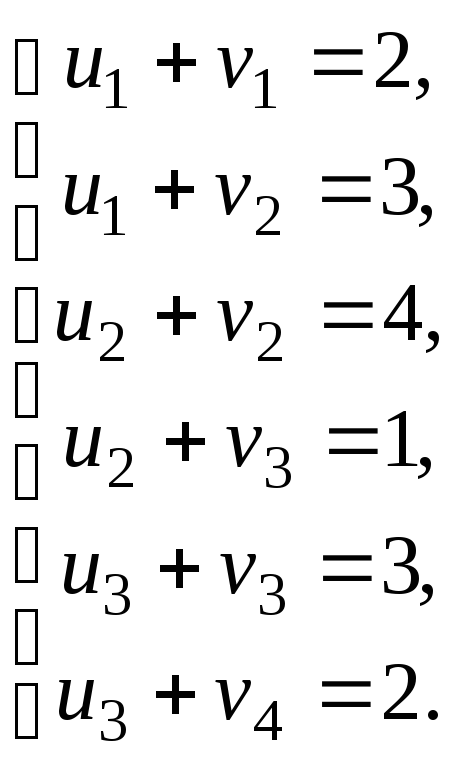
Маємо
,
,
,
,
,
,
.
Легко
обчислити оцінки
і побудувати матрицю
оцінок
.
Умови
оптимальності найбільше не задовольняються
в клітинці (3;2), бо
.
Будуємо
цикл і здійснюємо перерахунок плану.
.
Далі не
будемо виписувати в таблиці об’єми
запасів та потреб, а замість них
вписуватимемо потенціали
та
,
розраховані усно за новим планом. У
правому нижньому кутку таблиці будемо
замість
вписувати
величину затрат, відповідну новому
плану. Побудований цикл зображатимемо
в таблиці:
-
20
2
6
–3
3
+
1
0
1
6
4
25
1
3
1
2
3
+2
3
20 –
2
-1
2
3
0
3
153
.
Побудуємо
цикл із вершиною в клітинці
.
Тут
,
.
Отримуємо новий план
-
2
0–2
3
3
6
+1
0
+
1
6
–4
25
1
3
3
2
9
+2
3
14–
2
1
2
1
-2
1
141
,
,
.
-
1
4
–2
3
3
1
2
+1
0
6
1
4
25
1
3
-1
+
2
15
2
3
8 –
2
1
2
1
2
1
117
,
.
-
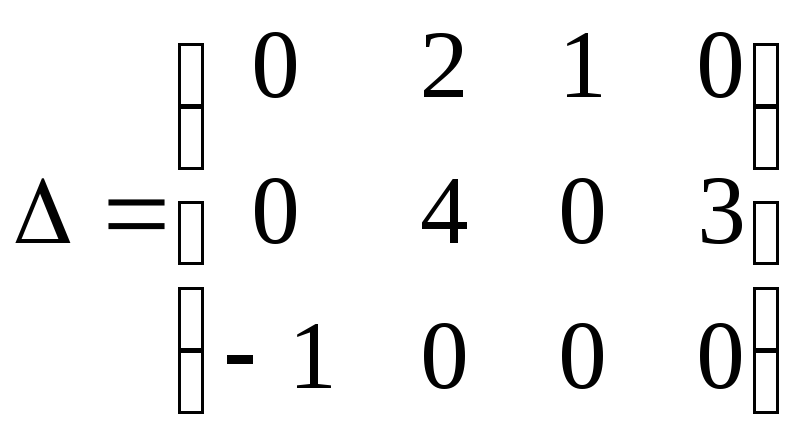
6
2
3
3
20
1
0
6
1
4
25
1
3
-1
8
2
15
2
3
2
0
2
2
0
1
109
.
Усі
невід’ємні. Отже, отриманий план
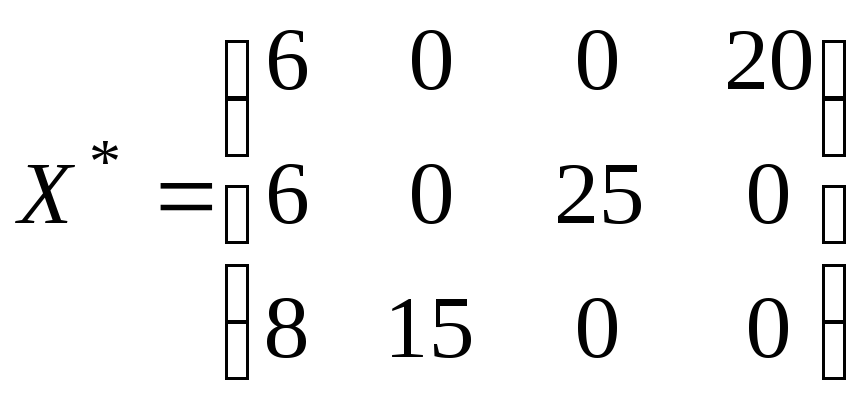
оптимальний.
Мінімальні затрати на перевезення
.
Приклад 2. Розв’язати транспортну задачу
-
2
2
1
3
20
3
1
3
2
15
1
2
1
1
35
10
20
20
20
70
Зрозуміло, що задача вироджена, бо
,
.
Розв’яжемо збурену задачу
-
2
2
1
3
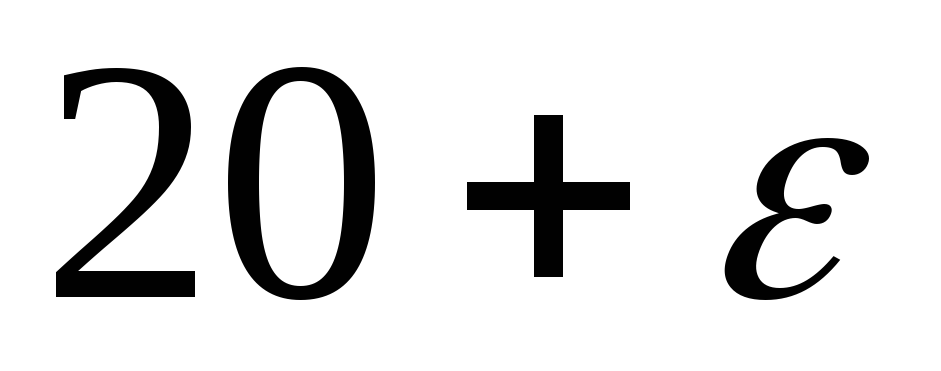
3
1
3
2
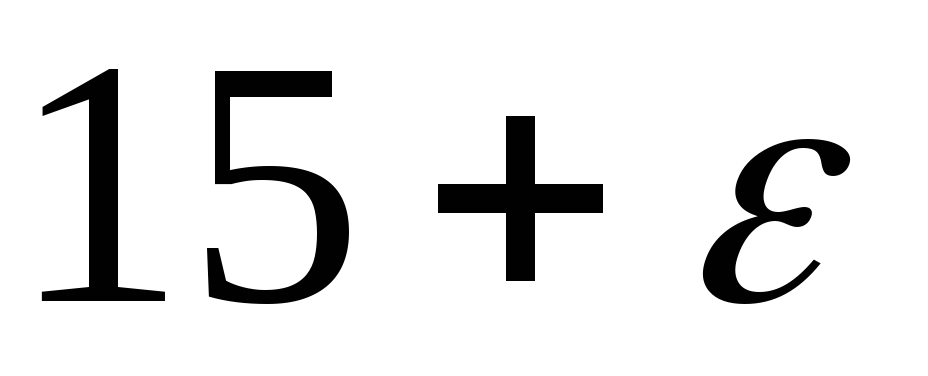
1
2
1
1
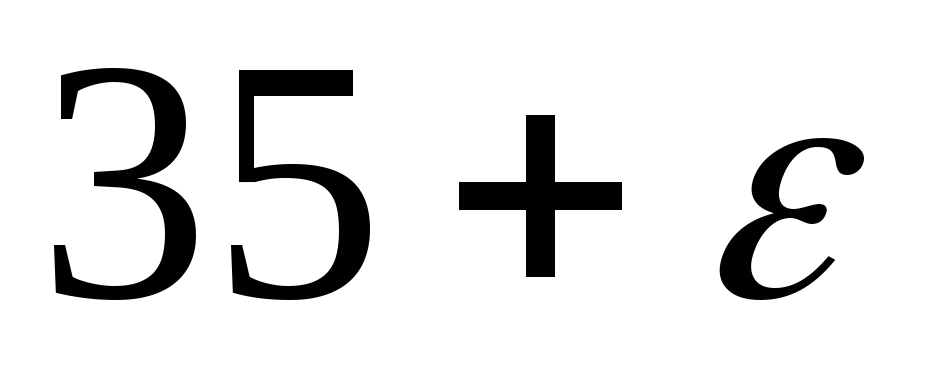
10
20
20
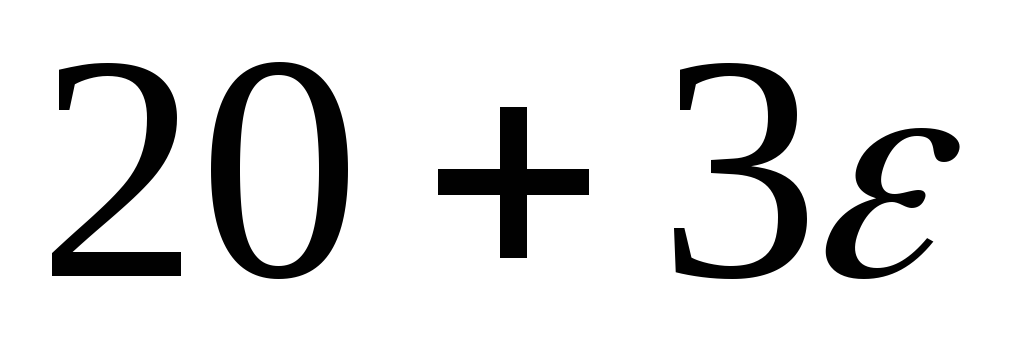
Методом північно-західного кута знаходимо початковий план і в подальшому замість запасів і потреб у таблиці виписуємо потенціали.
-
10
2
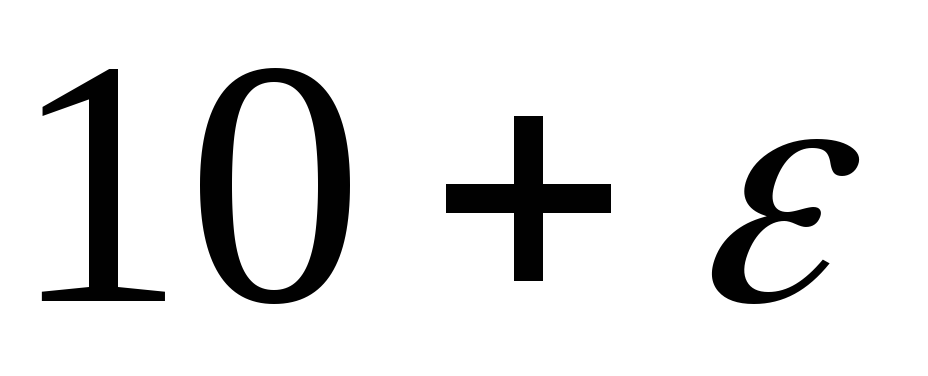
–2
+
1
3
0
3
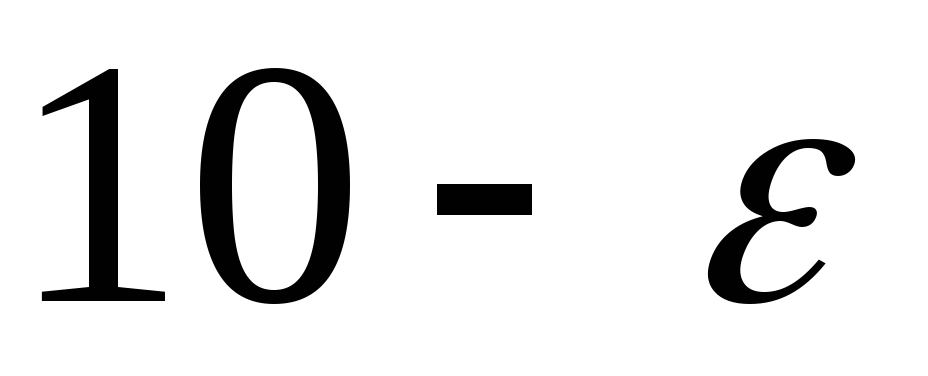
+1
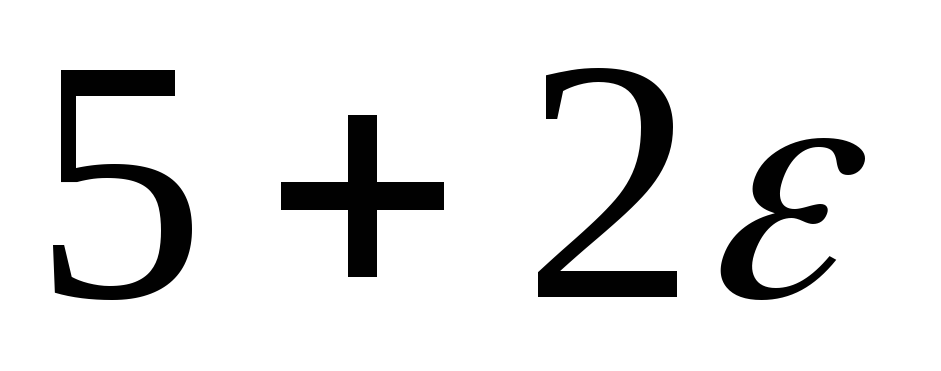–3
2
-1
1
2
1
1
-3
2
2
4
4
.
,
.
-
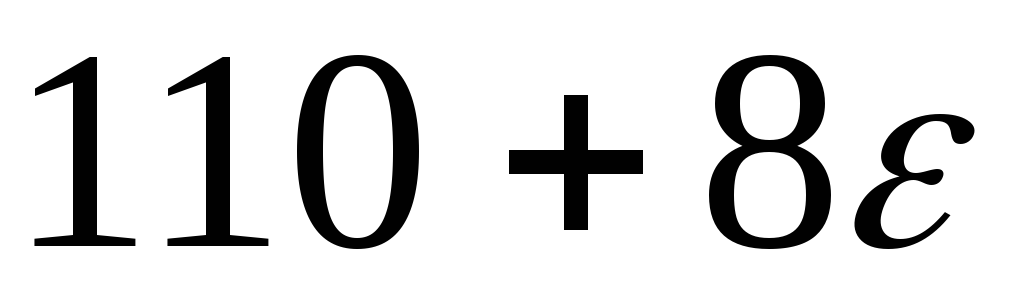
1
0–2
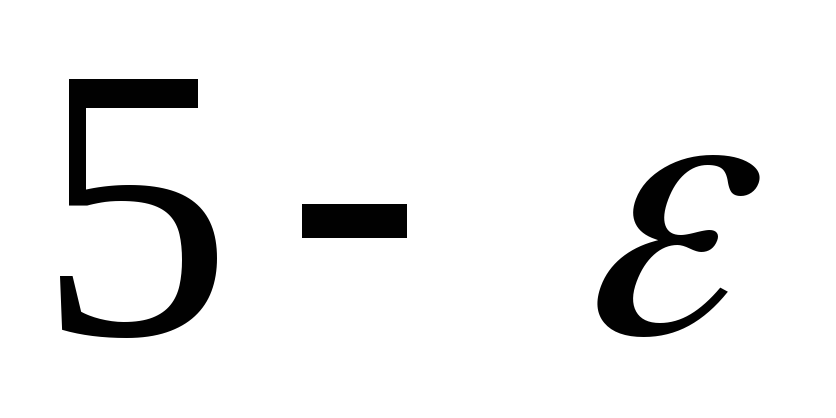
2
+1
3
0
3
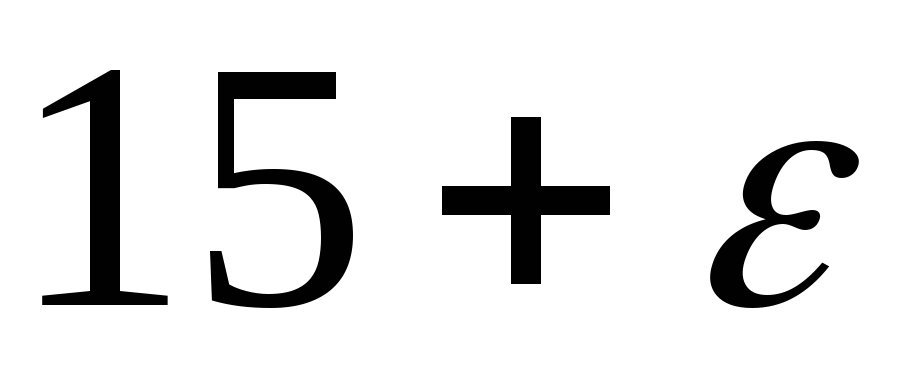
1
3
2
-1
+
1
2
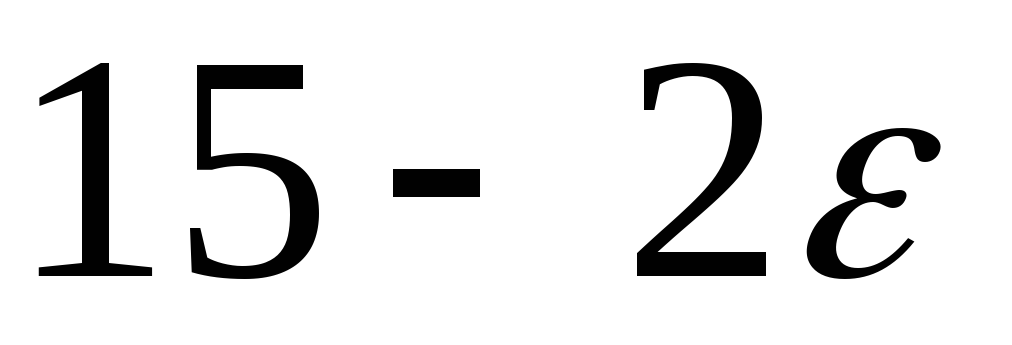–1
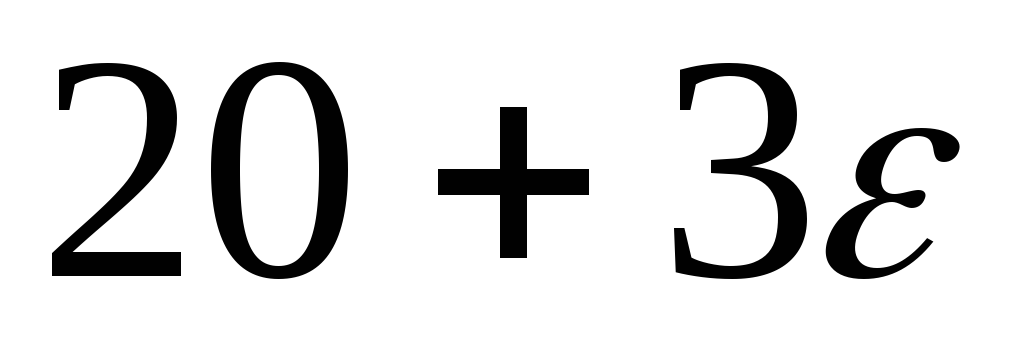
1
0
2
2
1
1
.
,
.
-
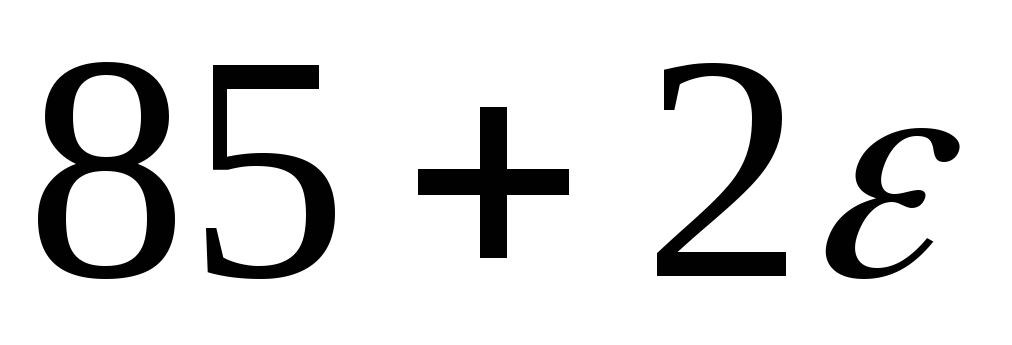
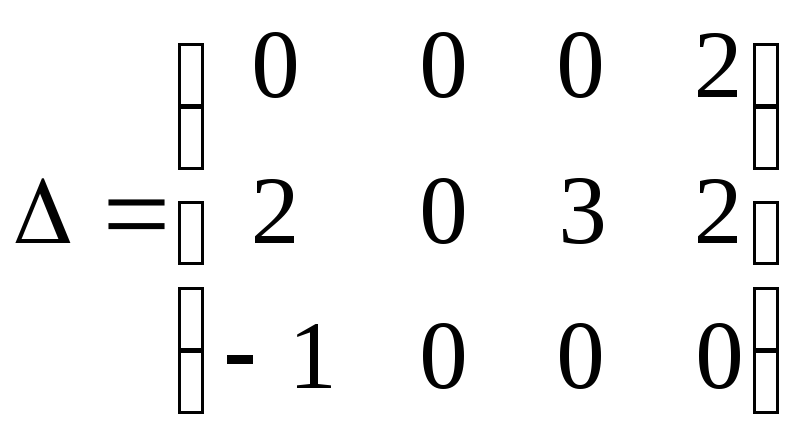2
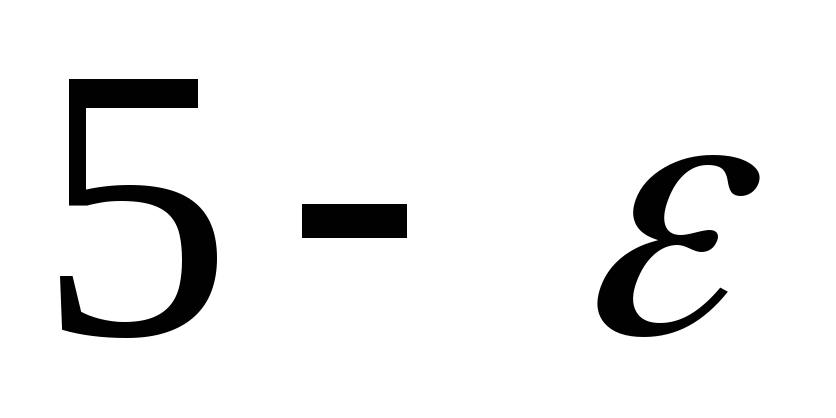
2
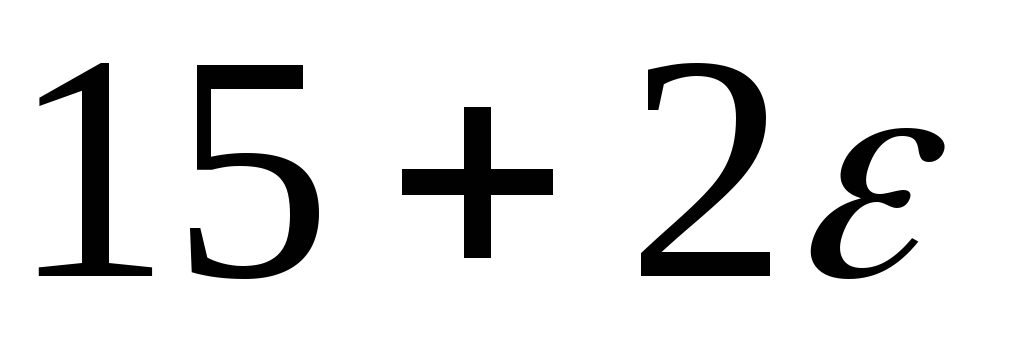
1
3
0
3
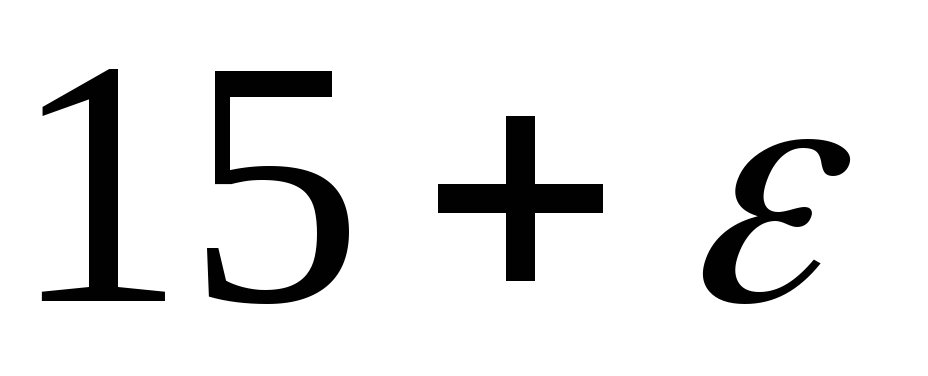
1
3
2
-1
10
1
2
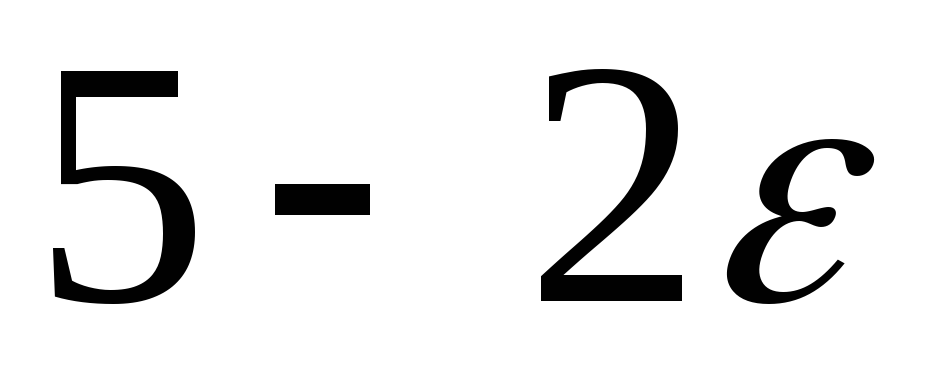
1
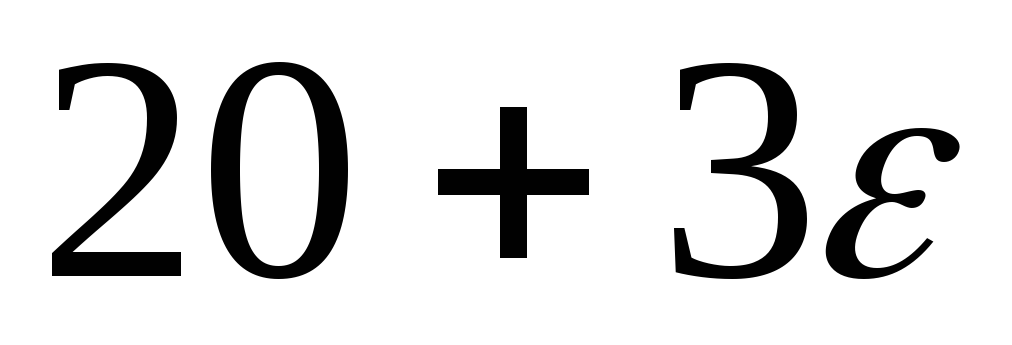
1
0
1
2
1
1
,
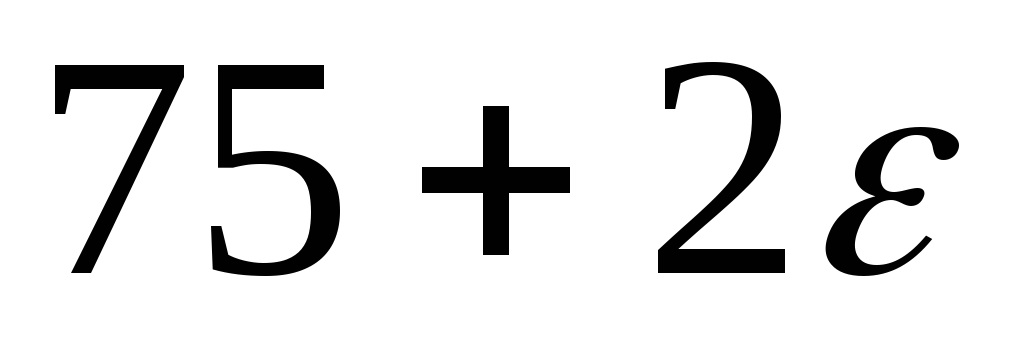
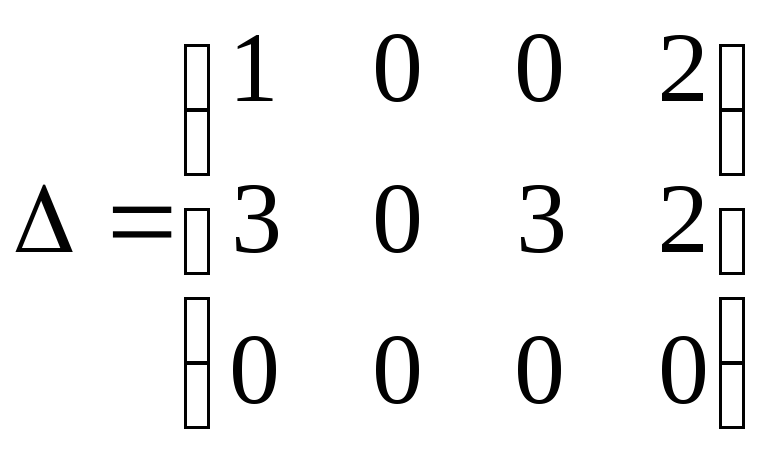всі
.
Оптимальним планом збуреної задачі є
.
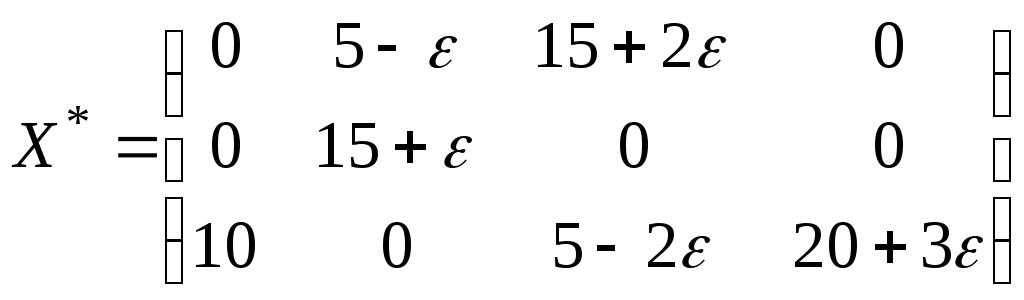Вважаючи,
що
,
отримуємо оптимальний план заданої
задачі
.
При
цьому
.
Зазначимо, що оптимальний план виявився невиродженим, хоча існують і невироджені базисні плани, наприклад
.
Зауваження.
На практиці часто появляються задачі
лінійного програмування з двосторонніми
обмеженнями на пропускні здатності
комунікацій (шляхів сполучення). Ми
розглянули лише випадки
,
.
Загальні властивості задач із двосторонніми
обмеженнями можна отримати, включивши
обмеження вигляду
чи
у непрямі обмеження. Наявність цих
обмежень вносить в алгоритми розв’язування
задач деякі зміни, часом істотні. І
загальні властивості можуть дещо
змінюватися. Зокрема, якщо у транспортній
задачі пропускні здатності
малі в порівнянні з потребами, то
розв’язку задачі може не існувати.