§ 13. Свойства функций, непрерывных в замкнутом промежутке
1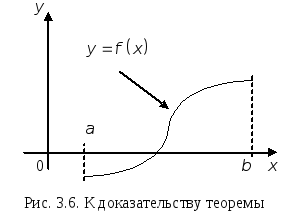
.
Первая теорема Больцано-Коши (теорема
об обращении функции в нуль).
Пусть функция
определена и непрерывна в замкнутом
промежутке
.
Если значения функции на концах промежутка
суть числа разных знаков (т. е.
),
то между точками
и
обязательно найдется хотя бы одна точка
такая, что
.
На рис. 3.6. дано геометрическое пояснение; оно не является доказательством теоремы.
► Пусть для
определенности
,
.
Положим
.
Если окажется, что
,
то точка
будет искомой.
Пусть же
.
Тогда один и только один из двух
промежутков
,
будет таким, у которого на левом конце
функция
принимает отрицательное значение, а на
правом — положительное. Обозначим этот
промежуток
.
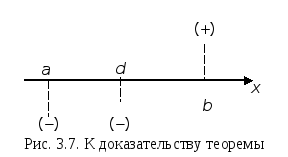
Если реализуется
случай 1) (см. рис. 3.7), то
.
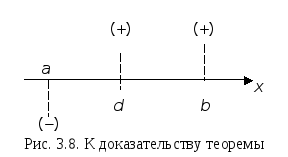
Если реализуется случай 2) (см. рис. 3.8),
то
.
Ясно, что
и что
;
.
Положим, затем
.
Если окажется, что
,
то точка
будет искомой.
Пусть же
.
Тогда один и только один из двух
промежутков
,
будет таким, у которого на левом конце
функция
принимает отрицательное значение, а на
правом — положительное. Обозначим этот
промежуток
.
Будем иметь:
;
,
;
,
.
Станем продолжать
этот процесс аналогичным образом. Если
на каком-нибудь шаге мы получим точку
такую, что
,
то эта точка
будет искомой. В противном случае мы
получим две бесконечные последовательности
(1)
и
.
(2)
такие что при всех
:
,
,
.
Так как
,
а
,
то при всех
:
.
Значит последовательность (1) монотонно
возрастает (по крайней мере, в широком
смысле) и ограничена сверху. Следовательно,
у последовательности (1) существует
конечный предел. Пусть
.
У нас при всех
.
Переходя здесь к пределу при
,
получим:
,
т. е.
.
Покажем, что
последовательность (2) сходится к тому
же пределу
.
В самом деле, имеем
.
Так как
,
то
.
Итак, показано,
что в промежутке
существует точка
такая, что
и
.
По условию функция
непрерывна в промежутке
.
Значит, в частности, функция
будет непрерывна в точке
.
Но тогда из соотношений
,
следует
и
.
У нас при всех
:
.
(3)
Переходя в
неравенствах (3) к пределу при
,
получим
.
Совместное
осуществление этих двух неравенств
возможно лишь тогда, когда
.
Было показано, сто точка
.
Так как по условию
и
,
то заключаем, что
,
т. е.
.
◄
|
|
|
Рис. 3.9. К замечанию. |
во всех точках промежутка
существенно. Возьмем, например, функцию
и рассмотрим ее в промежутке
(рис. 3.9). Хотя эта функция и принимает
значения разных знаков на концах
промежутка
,
но в нуль в
нигде не обращается. Эта функция не
является непрерывной в точке
.
2. Вторая теорема
Больцано-Коши (теорема о промежуточном
значении).
Пусть функция
определена и непрерывна в замкнутом
промежутке
и на концах этого промежутка принимает
не равные значения. (пусть для определенности
).
Тогда, какое бы число
,
лежащее между
и
ни взять (
),
между точками
и
обязательно найдется хотя бы одна точка
такая, что будет
.
Иначе: непрерывная функция, переходя от одного своего значения к другому, принимает и все промежуточные значения.
► Введем в
рассмотрение вспомогательную функцию:
.
Ясно, что функция
определена и непрерывна в замкнутом
промежутке
.
У нас
.
Поэтому
.
Видим, что функция
на концах промежутка
принимает значения разных знаков. А
тогда, по первой теореме Больцано-Коши,
между точками
и
обязательно найдется хотя бы одна точка
такая, что будет
,
т. е.
или
.
◄