
- •Глава 3 Предельное значение функции. Непрерывность § 1. Предел функции
- •§ 2. Односторонние пределы функции
- •§ 3. Предел отношения синуса к своей дуге
- •§ 4. Число e
- •§ 5. Предел функции при
- •§ 6. Натуральные логарифмы. Показательная функция . Гиперболические функции
- •§ 7. Бесконечно малые и бесконечно большие функции
- •§ 8. Свойства конечных пределов, связанные с арифметическими действиями над функциями
- •§ 9. Сравнение бесконечно малых функций
- •§ 10. Непрерывность функций
- •§ 11. Свойства непрерывных функций
- •2. Арифметические операции над непрерывными функциями.
- •3. Непрерывность сложной функции.
- •§ 12. Непрерывность элементарных функций
- •§ 13. Свойства функций, непрерывных в замкнутом промежутке
- •§ 14. Понятие обратной функции
- •§ 15. Непрерывность элементарных функций (продолжение)
- •§ 16. Три важных предела
- •§ 17. Степенно-показательные выражения
- •§ 18. Теоремы Вейерштрасса
- •§ 19. Понятие равномерной непрерывности функции. Теорема Кантора
- •§ 20. Точки разрыва функций и их классификация
2. Арифметические операции над непрерывными функциями.
Теорема.
Пусть функции
![]() и
и
![]() определены в промежутке
определены в промежутке
![]() и непрерывны в точке
и непрерывны в точке
![]() .
Тогда в точке
.
Тогда в точке
![]() будут непрерывны также функции:
будут непрерывны также функции:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
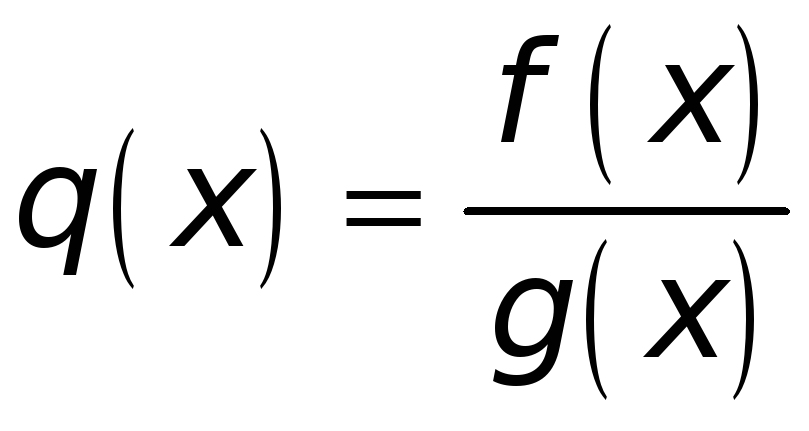 (частное при условии:
(частное при условии:
![]() ).
).
► В случае частного
![]() .
А тогда по теореме о стабильности знака
.
А тогда по теореме о стабильности знака
![]() для
для
![]() и удовлетворяющих условию
и удовлетворяющих условию
![]() .
Следовательно,
.
Следовательно,
 определена для
определена для
![]() (
(![]() ).
Установим, например, непрерывность в
точке
).
Установим, например, непрерывность в
точке
![]() функции
функции
 .
По условию
.
По условию
![]() и
и
![]() непрерывны в точке
непрерывны в точке
![]() .
Значит,
.
Значит,
![]() ,
,
![]() (
(![]() и
и
![]() — определенные числа).
— определенные числа).
Но тогда по теореме
о пределе частного двух функций (так
как предел знаменателя
![]() ),
имеем:
),
имеем:
 .
.
А это равенство
означает, что функция
![]() непрерывна в точке
непрерывна в точке
![]() . ◄
. ◄
3. Непрерывность сложной функции.
Определение.
Пусть функция
![]() определена в некотором промежутке
определена в некотором промежутке
![]() ,
а функция
,
а функция
![]() определена в промежутке
определена в промежутке
![]() и такая, что, если
и такая, что, если
![]() ,
то
,
то
![]() .
Тогда для
.
Тогда для
![]() имеет смысл выражение
имеет смысл выражение
![]() .
Выражение
.
Выражение
![]() представляет собой функцию аргумента
представляет собой функцию аргумента
![]() ,
определенную в промежутке
,
определенную в промежутке
![]() .
Эта функция называется сложной
функцией
или суперпозицией
функций
.
Эта функция называется сложной
функцией
или суперпозицией
функций
![]() и
и
![]() .
.
Замечание.
Предположение, что значения функции
![]() не выходят за пределы промежутка
не выходят за пределы промежутка
![]() ,
в котором определена функция
,
в котором определена функция
![]() ,
весьма существенно: если его опустить,
то может получиться и нелепость. Например.
полагая
,
весьма существенно: если его опустить,
то может получиться и нелепость. Например.
полагая
![]() ,
а
,
а
![]() ,
мы можем рассматривать лишь такие
значения
,
мы можем рассматривать лишь такие
значения
![]() ,
для которых
,
для которых
![]() ,
ибо иначе выражение
,
ибо иначе выражение
![]() не имело бы смысла.
не имело бы смысла.
Теорема.
Суперпозиция непрерывных функций
непрерывна, т.е. если функция
![]() непрерывна в некоторой точке
непрерывна в некоторой точке
![]() ,
а функция
,
а функция
![]() непрерывна в соответствующей точке
непрерывна в соответствующей точке
![]() (
(![]() ),
то суперпозиция
),
то суперпозиция
![]() непрерывна в точке
непрерывна в точке
![]() .
.
► Возьмем
последовательность
![]() любую, но такую, что
любую, но такую, что
![]() и
и
![]() .
Тогда, в силу непрерывности функции
.
Тогда, в силу непрерывности функции
![]() в точке
в точке
![]() ,
будет
,
будет
![]() ,
т.е.
,
т.е.
![]() .
.
(т.к.
![]() ,
то
,
то
![]() при всех
при всех
![]() ).
Т.к.
).
Т.к.
![]() и
и
![]() ,
то, в силу непрерывности функции
,
то, в силу непрерывности функции
![]() в точке
в точке
![]() ,
будет:
,
будет:
![]() ,
т.е
,
т.е
![]() ,
т.е.
,
т.е.
![]() .
А это и означает, что функция
.
А это и означает, что функция
![]() непрерывна в точке
непрерывна в точке
![]() .
◄
.
◄
§ 12. Непрерывность элементарных функций
1.
![]() .
Эта функция непрерывна в любой точке
.
Эта функция непрерывна в любой точке
![]() .
.
► В самом деле,
пусть точка
![]() — любая из
— любая из
![]() .
Возьмем последовательность
.
Возьмем последовательность
![]() любую, но такую, что
любую, но такую, что
![]() .
Соответствующая последовательность
значений функции будет такой:
.
Соответствующая последовательность
значений функции будет такой:
![]()
Значит,
![]() .
А это означает, что
.
А это означает, что
![]() — непрерывна в точке
— непрерывна в точке
![]() .
У нас точка
.
У нас точка
![]() — любая из промежутка
— любая из промежутка
![]() .
Следовательно,
.
Следовательно,
![]() — непрерывна в промежутке
— непрерывна в промежутке
![]() .
◄
.
◄
2.
![]() .
Эта функция непрерывна в любой точке
.
Эта функция непрерывна в любой точке
![]() .
.
► Выберем и закрепим
любую точку
![]() из
из
![]() .
Возьмем последовательность
.
Возьмем последовательность
![]() любую, но такую, что
любую, но такую, что
![]() .
Соответствующая последовательность
значений функции будет такой:
.
Соответствующая последовательность
значений функции будет такой:
![]()
Значит,
![]() .
А это означает, что
.
А это означает, что
![]() — непрерывна в точке
— непрерывна в точке
![]() .
У нас точка
.
У нас точка
![]() — любая из промежутка
— любая из промежутка
![]() .
Следовательно,
.
Следовательно,
![]() — непрерывна в промежутке
— непрерывна в промежутке
![]() .
◄
.
◄
3.
![]() .
.
► Эта функция
непрерывна в любой точке
![]() ибо
ибо
![]() .
.
Следовательно,
![]() непрерывна в промежутке
непрерывна в промежутке
![]() как произведение конечного числа
функций, непрерывных в этом промежутке. ◄
как произведение конечного числа
функций, непрерывных в этом промежутке. ◄
4.
![]() (
(![]() — целая рациональная функция, полином).
— целая рациональная функция, полином).
► Эта функция
непрерывна в любой точке
![]() как сумма конечного числа функций,
непрерывных в этом промежутке. ◄
как сумма конечного числа функций,
непрерывных в этом промежутке. ◄
5.

![]() и
и
![]()
![]() (
(![]() — целая рациональная функция, полином).
— целая рациональная функция, полином).
► Эта функция, как
отношение двух непрерывных функций,
будет непрерывна в любой точке
![]() ,
в которой знаменатель отличен от нуля;
т. е.
,
в которой знаменатель отличен от нуля;
т. е.
![]() будет непрерывна в каждой точке области
своего существования. ◄
будет непрерывна в каждой точке области
своего существования. ◄
Лемма.
Для всех вещественных значений
![]() справедливо неравенство
справедливо неравенство
![]() (*)
(*)
► 1) Если
![]() ,
то соотношение (*) справедливо (это
очевидно).
,
то соотношение (*) справедливо (это
очевидно).
2) Пусть
![]() .
При доказательстве соотношения
.
При доказательстве соотношения
![]() было получено неравенство
было получено неравенство
![]() ,
если
,
если
![]() .
Так как
.
Так как
![]() и
и
![]() для
для
![]() ,
то
,
то
![]() и потому неравенство
и потому неравенство
![]() может быть записано в виде
может быть записано в виде
![]() .
Следовательно, соотношение (*) справедливо
для значений
.
Следовательно, соотношение (*) справедливо
для значений
![]() ,
удовлетворяющих условию
,
удовлетворяющих условию
![]() .
.
3) Пусть
![]() .
Имеем в этом случае
.
Имеем в этом случае
![]() .
Так как всегда
.
Так как всегда
![]() ,
то получаем
,
то получаем
![]() .
Значит соотношение (*) справедливо для
значений
.
Значит соотношение (*) справедливо для
значений
![]() .
.
4) Пусть
![]() ,
т. е.
,
т. е.
![]() .
Имеем
.
Имеем
![]() ;
;
![]() ,
если
,
если
![]() .
В п.п.2) и 3) было доказано:
.
В п.п.2) и 3) было доказано:
![]() ,
если
,
если
![]() .
Значит
.
Значит
![]() ,
если
,
если
![]() .
.
Показано,
следовательно, что соотношение (*)
справедливо и для значений
![]() .
◄
.
◄
6.
![]() .
Утверждаем, что
.
Утверждаем, что
![]() непрерывна в промежутке
непрерывна в промежутке
![]() .
.
► Выберем и закрепим
любую точку
![]() из промежутка
из промежутка
![]() .
Возьмем последовательность
.
Возьмем последовательность
![]() любую, но такую, что
любую, но такую, что
![]() (а значит
(а значит
![]() ).
Этой последовательности значений
аргумента будет соответствовать
последовательность значений функции:
).
Этой последовательности значений
аргумента будет соответствовать
последовательность значений функции:
![]() .
Имеем
.
Имеем
![]()
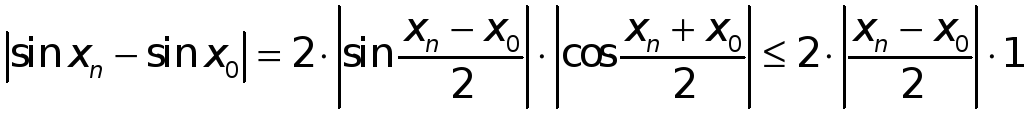 .
.
Таким образом, получили
![]() .
.
У нас
![]() А тогда, по теореме о «сжатой переменной»,
находим, что
А тогда, по теореме о «сжатой переменной»,
находим, что
![]() .
Так как последнее соотношение справедливо
для любой последовательности
.
Так как последнее соотношение справедливо
для любой последовательности
![]() ,
сходящейся к
,
сходящейся к
![]() ,
то заключаем, что
,
то заключаем, что
![]() .
А это означает, что функция
.
А это означает, что функция
![]() непрерывна в точке
непрерывна в точке
![]() .
У нас точка
.
У нас точка
![]() — любая из промежутка
— любая из промежутка
![]() .
Следовательно, функция
.
Следовательно, функция
![]() непрерывна в промежутке
непрерывна в промежутке
![]() .
◄
.
◄
7.
![]() .
Утверждаем, что
.
Утверждаем, что
![]() непрерывна в промежутке
непрерывна в промежутке
![]() .
.
► Известно, что
 .
Следовательно, функция
.
Следовательно, функция
![]() непрерывна в промежутке
непрерывна в промежутке
![]() как суперпозиция двух непрерывных
функций. ◄
как суперпозиция двух непрерывных
функций. ◄
8.
![]() .
.
► Имеем
![]() — непрерывна как отношение двух
непрерывных функций на всей вещественной
оси, за исключением точек, в которых
— непрерывна как отношение двух
непрерывных функций на всей вещественной
оси, за исключением точек, в которых
![]() ,
т.е. за исключением точек
,
т.е. за исключением точек
![]() .
таким образом, функция
.
таким образом, функция
![]() непрерывна в каждой точке области своего
существования. ◄
непрерывна в каждой точке области своего
существования. ◄
9.
![]() .
.
► Имеем
![]() — непрерывна как отношение двух
непрерывных функций на всей вещественной
оси, за исключением точек, в которых
— непрерывна как отношение двух
непрерывных функций на всей вещественной
оси, за исключением точек, в которых
![]() ,
т.е. за исключением точек
,
т.е. за исключением точек
![]() .
таким образом, функция
.
таким образом, функция
![]() непрерывна в каждой точке области своего
существования. ◄
непрерывна в каждой точке области своего
существования. ◄
