§ 5. Предел функции при
1.
Установим сначала, что
.
На этот раз воспользуемся определением
предела функции "на языке
последовательностей".
► Составим
последовательность
— любую, но такую, что
и
.
Соответствующая последовательность
значений функции будет такой:
.
Выше мы показали, что
.
Так как
— любая последовательность, удовлетворяющая
условиям
и
,
то в соответствии с определением предела
функции"на языке последовательностей"
можно написать
.
◄
2.
покажем
теперь, что и
.
► Составим
последовательность
— любую, но такую, что
и
.
Если положить
,
то
при
(и все
).
Имеем
=
.
Так как
и
,
то получаем
.
Так как
— любая последовательность, удовлетворяющая
условиям
и
,
то в соответствии с определением предела
функции «на языке последовательностей»
можно написать
.
◄
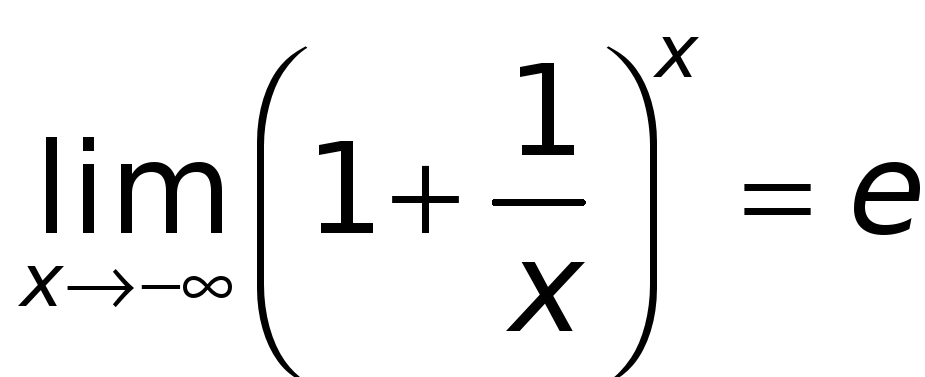В выражении
заменим переменную
на
.
Получим функцию
.
Возьмем
последовательность
— любую, но такую, что
и
.
Тогда
и, следовательно,
.
А это означает,
что
.
Возьмем теперь
последовательность
— любую, но такую, что
и
.
Но тогда
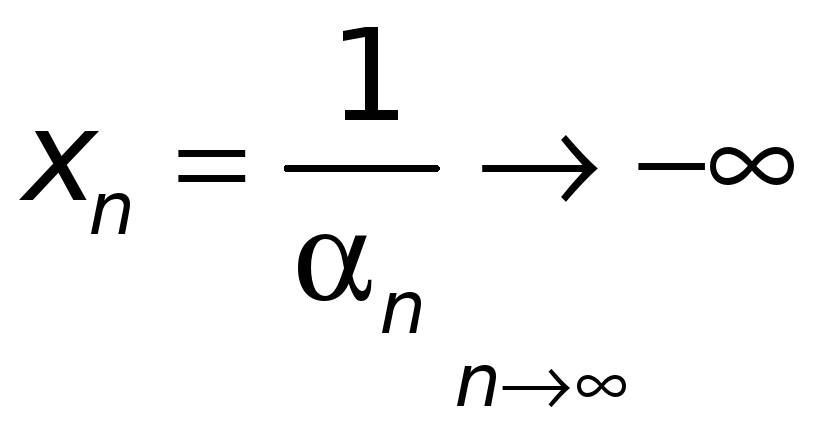и, следовательно,
.
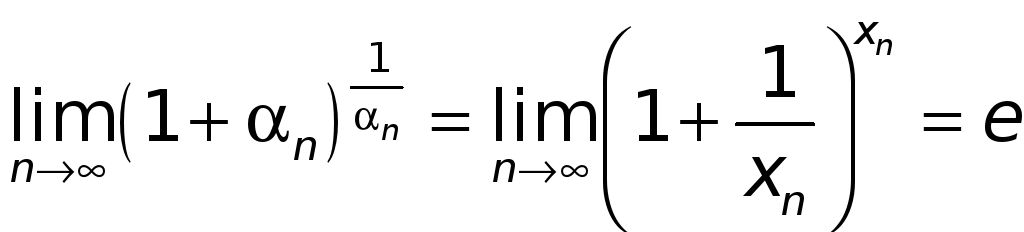А это означает,
что
.
Так как правый и
левый пределы функции
в точке
существуют и равны
,
то у этой функции в точке
существует обычный (двусторонний)
предел, и он равен
.
Таким образом, установлено, что
.
Отметим, что
полученный результат лежит в основе
всех приложений числа
.
§ 6. Натуральные логарифмы. Показательная функция . Гиперболические функции
Некоторые свойства числа е, которые будут установлены позже, делают выгодным выбор этого числа в качестве основания для системы логарифмов.
Определение.
Логарифм числа х
(х
> 0) вычисленный по основанию е,
называют натуральным логарифмом и
обозначают знаком:
(без указания основания), т. е.
.
Установим связь между натуральным логарифмом числа е и логарифмом этого числа по основанию а (а > 0, а ≠ 1).
Имеем
.
Прологарифмируем это равенство по
основанию а.
Получим
(
— модуль перехода). В частности, если а
= 10, то будем иметь
,
где
.
Такова связь между десятичными и натуральными логарифмами.
Известно, что если
,
то
— показательная функция. На рис. 3.2
показаны графики этой функции при
различных значениях
(
и
).
Если
,
то получим показательную функцию
— экспоненту.
|
|
|
Рис. 3.2. Показательная функция |
тесно связаны гиперболические функции,
представляющие интерес в технических
приложениях математики.
1. Гиперболический
синус
.
Так называют функцию вида (рис. 3.3)
.
|
|
|
Рис. 3.3. Функции
|
и
;
область изменения:
.
2. Гиперболический
синус
.
Так называют функцию вида (рис. 3.3)
.
Область существования:
;
область изменения:
.
3. Гиперболический
тангенс
.
Так называют функцию вида (рис. 3.4)
.
Область существования:
;
область изменения:
.
4. Гиперболический
котангенс
.
Так называют функцию вида (рис. 3.4)
|
|
|
Рис. 3.4. Функции
|
и
.
Область существования:
;
область изменения:
.
Эти функции проявляют замечательную аналогию с тригонометрическими функциями. Так, имеют место формулы (обратите внимание на знаки!)
,
,
из которых при
,
в частности, следует
,
.