
- •Глава 3 Предельное значение функции. Непрерывность § 1. Предел функции
- •§ 2. Односторонние пределы функции
- •§ 3. Предел отношения синуса к своей дуге
- •§ 4. Число e
- •§ 5. Предел функции при
- •§ 6. Натуральные логарифмы. Показательная функция . Гиперболические функции
- •§ 7. Бесконечно малые и бесконечно большие функции
- •§ 8. Свойства конечных пределов, связанные с арифметическими действиями над функциями
- •§ 9. Сравнение бесконечно малых функций
- •§ 10. Непрерывность функций
- •§ 11. Свойства непрерывных функций
- •2. Арифметические операции над непрерывными функциями.
- •3. Непрерывность сложной функции.
- •§ 12. Непрерывность элементарных функций
- •§ 13. Свойства функций, непрерывных в замкнутом промежутке
- •§ 14. Понятие обратной функции
- •§ 15. Непрерывность элементарных функций (продолжение)
- •§ 16. Три важных предела
- •§ 17. Степенно-показательные выражения
- •§ 18. Теоремы Вейерштрасса
- •§ 19. Понятие равномерной непрерывности функции. Теорема Кантора
- •§ 20. Точки разрыва функций и их классификация
§ 17. Степенно-показательные выражения
Это выражения вида
![]() (*)
(*)
Здесь
![]() и
и
![]() — функции от
— функции от
![]() ,
определенные на множестве
,
определенные на множестве
![]() .
Предполагаем, что для всех
.
Предполагаем, что для всех
![]() из множества
из множества
![]() :
:
![]() .
Пусть требуется найти предел выражения
.
Пусть требуется найти предел выражения
![]() при
при
![]() .
Считаем, что точка
.
Считаем, что точка
![]() обладает тем свойством, что в любой
обладает тем свойством, что в любой
![]() -окрестности
точки
-окрестности
точки
![]() имеются точки множества
имеются точки множества
![]() ,
отличные от
,
отличные от
![]() .
Представим выражение (*) в виде
.
Представим выражение (*) в виде
![]() .
.
Пусть существуют
конечные пределы:
![]() и
и
![]() ,
причем
,
причем
![]() (значит, существует конечный предел
(значит, существует конечный предел
![]() ;
здесь использована непрерывность
логарифмической функции). Следовательно,
;
здесь использована непрерывность
логарифмической функции). Следовательно,
![]() .
.
А тогда, в силу непрерывности показательной функции, получаем
![]() .
.
Заметим, что предел
выражения
![]() при
при
![]() можно установить не только в случае,
рассмотренном выше, но и во всех случаях,
когда удается найти конечный или
бесконечный предел с
произведения
можно установить не только в случае,
рассмотренном выше, но и во всех случаях,
когда удается найти конечный или
бесконечный предел с
произведения
![]() ,
когда оно представляет неопределенность
вида
,
когда оно представляет неопределенность
вида
![]() при
при
![]() :
:
-
если с — конечное число, то
 ;
; -
если
 ,
то
,
то
 ;
; -
если
 ,
то
,
то
 .
.
Случаи, когда
произведение
![]() представляет при
представляет при
![]() неопределенность вида
неопределенность вида
![]() ,
отвечают следующим комбинациям:
,
отвечают следующим комбинациям:
-
 ,
,
 ;
; -
 ,
,
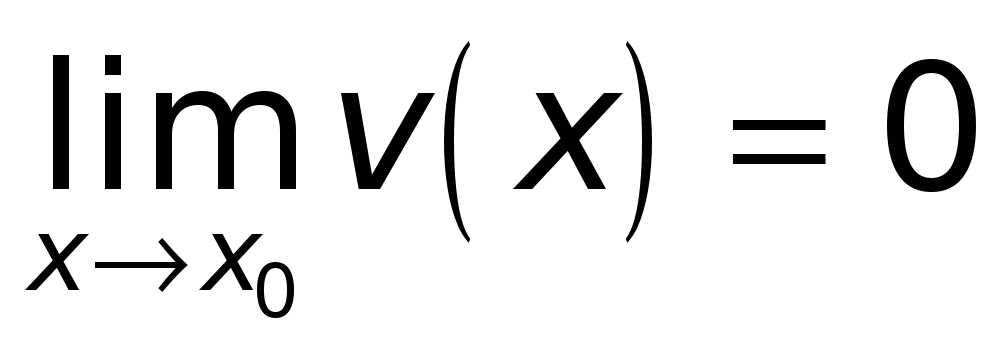 ;
; -
 ,
,
 .
.
В этих случаях
говорят, что выражение
![]() при
при
![]() представляет соответственно
неопределенности вида:
представляет соответственно
неопределенности вида:
![]() ,
,
![]() ,
,
![]() .
.
Для решения вопроса
о пределе выражения
![]() при
при
![]() здесь мало знать лишь пределы функций
здесь мало знать лишь пределы функций
![]() и
и
![]() при
при
![]() ,
а нужно непосредственно учитывать
законы, по которым они стремятся к своим
пределам при
,
а нужно непосредственно учитывать
законы, по которым они стремятся к своим
пределам при
![]() .
.
Приведем несколько примеров для раскрытия этих новых видов неопределенностей.
Пример 1.
Найти

►Имеем
 .
Станем искать
.
Станем искать
 .
.


 .
.
Ответ:
 .
◄
.
◄
Пример 2.
Найти

►Имеем
 .
Станем искать
.
Станем искать
 .
.
Положим
![]() ,
если
,
если
![]() .
Тогда
.
Тогда
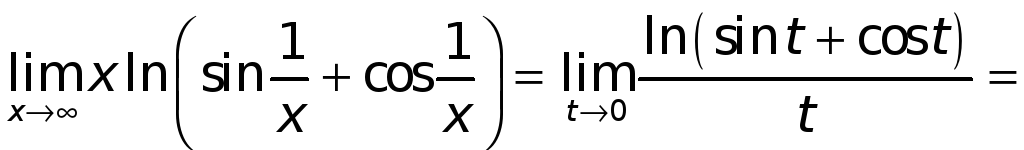


 .
.
§ 18. Теоремы Вейерштрасса
Первая теорема
Вейерштрасса (об ограниченности функции).
Если функция
![]() определена и непрерывна в замкнутом
промежутке
определена и непрерывна в замкнутом
промежутке
![]() ,
то она ограничена, т.е. существуют числа
,
то она ограничена, т.е. существуют числа
![]() и
и
![]() такие, что
такие, что
![]() для
для
![]() .
.
► Предположим
противное, а именно, допустим, что
![]() не
является ограниченной в промежутке
не
является ограниченной в промежутке
![]() .
Но тогда не может оказаться, чтобы для
всех
.
Но тогда не может оказаться, чтобы для
всех
![]() было бы:
было бы:
![]() .
Поэтому в промежутке
.
Поэтому в промежутке
![]() обязательно найдется хотя бы одно
обязательно найдется хотя бы одно
![]() такое, что будет:
такое, что будет:
![]() .
.
Точно также не
может оказаться, чтобы для всех
![]() было бы
было бы
![]() .
Поэтому в промежутке
.
Поэтому в промежутке
![]() обязательно найдется хотя бы одно
обязательно найдется хотя бы одно
![]() такое, что будет:
такое, что будет:
![]() .
.
и т. д.
Продолжая этот процесс, мы придем к последовательности
![]() (1)
(1)
такой, что при
каждом
![]() :
:
![]() и
и
![]() .
Но тогда
.
Но тогда
![]() (2)
(2)
У нас последовательность
(1) — ограниченная, ибо при любом
![]()
![]() (3)
(3)
Следовательно, по
принципу выбора Больцано-Вейерштрасса,
из последовательности (1) можно выделить
подпоследовательность, сходящуюся к
конечному пределу. Пусть это будет
![]() и пусть
и пусть
![]() .
Из неравенства (3) заключаем, что при
любом
.
Из неравенства (3) заключаем, что при
любом
![]() :
:
![]() .
.
Переходя здесь к
пределу при
![]() ,
получаем
,
получаем
![]() ,
т. е.
,
т. е.
![]() .
.
По условию функция
![]() непрерывна в
непрерывна в
![]() .
Значит, в частности,
.
Значит, в частности,
![]() непрерывна в точке
непрерывна в точке
![]() .
А тогда из того, что
.
А тогда из того, что
![]() ,
следует:
,
следует:
![]() (4)
(4)
(![]() — определенное число).
— определенное число).
С другой стороны,
последовательность
![]() является подпоследовательностью для
последовательности
является подпоследовательностью для
последовательности
![]() .
Из этого факта и из (2) вытекает, что
должно быть
.
Из этого факта и из (2) вытекает, что
должно быть
![]() (5)
(5)
Сопоставляя соотношения (4) и (5), видим, что получено противоречие. Это противоречие и доказывает теорему. ◄
Замечание.
Требование непрерывности функции
![]() в замкнутом промежутке
в замкнутом промежутке
![]() существенно. Если функция
существенно. Если функция
![]() непрерывна лишь в открытом промежутке
непрерывна лишь в открытом промежутке
![]() или в полуоткрытом промежутке
или в полуоткрытом промежутке
![]() (или
(или
![]() ),
то нельзя гарантировать ограниченность
),
то нельзя гарантировать ограниченность
![]() в этих промежутках.
в этих промежутках.
Рассмотрим,
например, функцию
![]() .
Она непрерывна в промежутке (0,1]. В каждой
конкретной точке этого промежутка она
принимает конечное значение, но
.
Она непрерывна в промежутке (0,1]. В каждой
конкретной точке этого промежутка она
принимает конечное значение, но
![]() — не ограничена, ибо при приближении х
к 0 может принимать сколь угодно большие
значения.
— не ограничена, ибо при приближении х
к 0 может принимать сколь угодно большие
значения.
Вторая теорема
Вейерштрасса (о наибольшем и наименьшем
значении). Если функция
![]() определена и непрерывна в замкнутом
промежутке
определена и непрерывна в замкнутом
промежутке
![]() ,
то она достигает в этом промежутке как
своего наибольшего, так и своего
наименьшего значений.
,
то она достигает в этом промежутке как
своего наибольшего, так и своего
наименьшего значений.
► По первой теореме
Вейерштрасса множество значений, которые
принимает функция
![]() на
на
![]() ,
является ограниченным. Мы знаем, что
для всякого непустого числового
множества, ограниченного и сверху, и
снизу, существуют точная верхняя и
точная нижняя границы.
,
является ограниченным. Мы знаем, что
для всякого непустого числового
множества, ограниченного и сверху, и
снизу, существуют точная верхняя и
точная нижняя границы.
Пусть
![]() (
(![]() и
и
![]() — конечные числа). Мы установим, что
функция
— конечные числа). Мы установим, что
функция
![]() достигает в промежутке
достигает в промежутке
![]() ,
например, своего наибольшего значения,
если покажем, что в промежутке
,
например, своего наибольшего значения,
если покажем, что в промежутке
![]() имеется хотя бы одна точка
имеется хотя бы одна точка
![]() такая, что
такая, что
![]() .
Рассуждаем от противного. Допустим, что
такой точки
.
Рассуждаем от противного. Допустим, что
такой точки
![]() в промежутке
в промежутке
![]() нет. Но тогда при всех х из промежутка
нет. Но тогда при всех х из промежутка
![]() будет:
будет:
![]() .
.
Введем в рассмотрение вспомогательную функцию
 .
.
Функция
![]() определена и непрерывна в промежутке
определена и непрерывна в промежутке
![]() как отношение двух непрерывных функций
с не обращающимся в нуль знаменателем.
Отметим еще, что
как отношение двух непрерывных функций
с не обращающимся в нуль знаменателем.
Отметим еще, что
![]() — положительная в
— положительная в
![]() .
.
К функции
![]() применима первая теорема Вейерштрасса.
Это позволяет утверждать, что существует
число
применима первая теорема Вейерштрасса.
Это позволяет утверждать, что существует
число
![]() такое, что при всех х из
такое, что при всех х из
![]() будет:
будет:
![]() или
или

![]() ,
для всех
,
для всех
![]() . (6)
. (6)
Так как неравенство
(6) выполняется для всех
![]() ,
то заключаем, что число
,
то заключаем, что число
![]() — есть верхняя граница множества
— есть верхняя граница множества
![]() ,
,
![]() .
А это невозможно, ибо у нас
.
А это невозможно, ибо у нас
![]() и, следовательно, любое число, меньшее,
чем М не является верхней границей
множества
и, следовательно, любое число, меньшее,
чем М не является верхней границей
множества
![]() ,
,
![]() .
Полученное противоречие доказывает,
что на промежутке
.
Полученное противоречие доказывает,
что на промежутке
![]() обязательно имеется хотя бы одна точка
обязательно имеется хотя бы одна точка
![]() ,
в которой функция
,
в которой функция
![]() принимает свое наибольшее значение.
принимает свое наибольшее значение.
Совершенно
аналогично устанавливается, что функция
![]() принимает в промежутке
принимает в промежутке
![]() свое наименьшее значение. ◄
свое наименьшее значение. ◄
