
- •Глава 3 Предельное значение функции. Непрерывность § 1. Предел функции
- •§ 2. Односторонние пределы функции
- •§ 3. Предел отношения синуса к своей дуге
- •§ 4. Число e
- •§ 5. Предел функции при
- •§ 6. Натуральные логарифмы. Показательная функция . Гиперболические функции
- •§ 7. Бесконечно малые и бесконечно большие функции
- •§ 8. Свойства конечных пределов, связанные с арифметическими действиями над функциями
- •§ 9. Сравнение бесконечно малых функций
- •§ 10. Непрерывность функций
- •§ 11. Свойства непрерывных функций
- •2. Арифметические операции над непрерывными функциями.
- •3. Непрерывность сложной функции.
- •§ 12. Непрерывность элементарных функций
- •§ 13. Свойства функций, непрерывных в замкнутом промежутке
- •§ 14. Понятие обратной функции
- •§ 15. Непрерывность элементарных функций (продолжение)
- •§ 16. Три важных предела
- •§ 17. Степенно-показательные выражения
- •§ 18. Теоремы Вейерштрасса
- •§ 19. Понятие равномерной непрерывности функции. Теорема Кантора
- •§ 20. Точки разрыва функций и их классификация
Глава 3 Предельное значение функции. Непрерывность § 1. Предел функции
Станем рассматривать
функцию
![]() ,
определенную на некотором множестве
,
определенную на некотором множестве
![]() ,
и точку а.
Точка а
может принадлежать, а может и не
принадлежать множеству X,
но обладает тем свойством, что в любой
,
и точку а.
Точка а
может принадлежать, а может и не
принадлежать множеству X,
но обладает тем свойством, что в любой
![]() -окрестности
точки а
имеются точки множества X,
отличные от а.
Например, точка а
может быть граничной точкой интервала,
на котором определена функция
-окрестности
точки а
имеются точки множества X,
отличные от а.
Например, точка а
может быть граничной точкой интервала,
на котором определена функция
![]() .
.
Определение 1 («на языке последовательностей»). Составляем последовательность значений аргумента х:
![]() ,
(1)
,
(1)
произвольную, но
такую, что
![]() и
и
![]() .
Последовательности (1) будет соответствовать
последовательность значений функции
.
Последовательности (1) будет соответствовать
последовательность значений функции
![]() :
:
![]() .
(2)
.
(2)
Если для любой
последовательности (1), сходящейся к а,
последовательность (2) имеет своим
пределом одно и то же число А,
то это число А
называется пределом
функции
![]() при
при
![]() .
.
Запись:
![]() ,
или
,
или
![]() при
при
![]() .
.
Замечание 1.
Условие
![]() ,
нужно для того, чтобы имело смысл говорить
о последовательности (2).
,
нужно для того, чтобы имело смысл говорить
о последовательности (2).
Замечание 2. Чтобы убедиться в справедливости соотношения:
![]() ,
,
недостаточно взять какую-нибудь последовательность (1), сходящуюся к а, и показать, что соответствующая последовательность (2) сходится к А. Нужно убедиться в том, что последовательность (2) сходится к А при любой последовательности (1), сходящейся к а.
Например, пусть
![]() .
Эта функция определена на множестве
.
Эта функция определена на множестве
![]() (т. е. определена на всей вещественной
оси, кроме точки х = 0).
Выясним, существует или нет
(т. е. определена на всей вещественной
оси, кроме точки х = 0).
Выясним, существует или нет
![]() .
.
Для этого возьмем
последовательность
 .
(Здесь
.
(Здесь
![]() ,
,
![]() ,
,
![]() ,
…,
,
…,
![]() ,
…) Видим, что
,
…) Видим, что
![]() и
и
![]() .
Соответствующая последовательность
значений функции будет такой:
.
Соответствующая последовательность
значений функции будет такой:
![]() .
.
Следовательно,
![]() .
.
Тем не менее,
соотношение
![]() неверно.
неверно.
В самом деле, возьмем другую последовательность

(Здесь
 ,
,
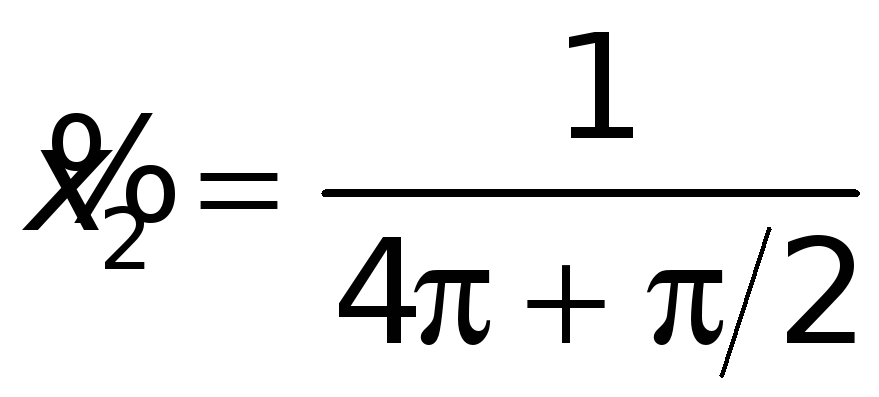 ,
,
 ,
…,
,
…,
 ,
… .) Видим, что
,
… .) Видим, что
![]() и
и
![]() ,
а соответствующая последовательность
значений функции
,
а соответствующая последовательность
значений функции
![]() ,
ибо
,
ибо
![]() .
.
Вывод:
![]() — не существует.
— не существует.
Рассмотрим теперь другой пример.
Пусть
 (корень арифметический). Эта функция
определена на множестве
(корень арифметический). Эта функция
определена на множестве
![]() .
Возьмем последовательность
.
Возьмем последовательность
![]() любую, но такую, что
любую, но такую, что
![]() (
(![]() )
и
)
и
![]() .
Для соответствующей последовательности
значений функции
.
Для соответствующей последовательности
значений функции
![]() :
:
 будем иметь:
будем иметь:

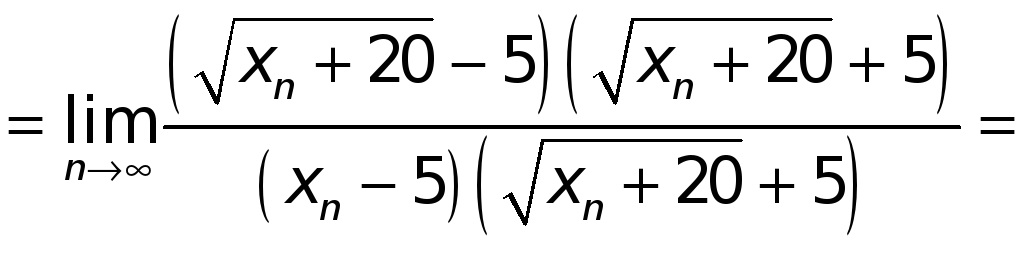
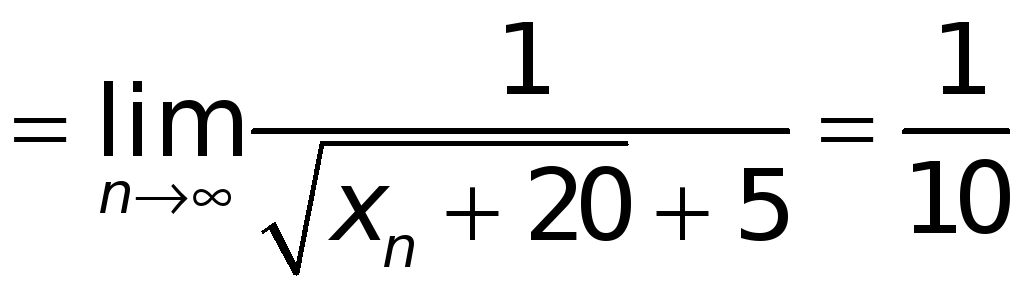 .
.
В этом примере
вычисление, приведшее нас к числу
![]() ,
использует лишь условия
,
использует лишь условия
![]() (
(![]() )
и
)
и
![]() ,
оставляя последовательность
,
оставляя последовательность
![]() в остальном произвольной. Значит, всякий
раз, когда
в остальном произвольной. Значит, всякий
раз, когда
![]() ,
пробегая любую последовательность
значений (лишь бы
,
пробегая любую последовательность
значений (лишь бы
![]() (
(![]() )),
величина
)),
величина
![]() пробегает последовательность, имеющую
своим пределом всегда одно и то же число
пробегает последовательность, имеющую
своим пределом всегда одно и то же число
![]() .
.
Вывод:
 .
.
Замечание 3.
В определении 1 предела функции
![]() а
и А
могут обозначать и числа, и символы
а
и А
могут обозначать и числа, и символы
![]() .
Если А
— число, то предел называется конечным.
Если же А
есть один из символов
.
Если А
— число, то предел называется конечным.
Если же А
есть один из символов
![]() ,
то предел называется бесконечным.
,
то предел называется бесконечным.
Определение 2
(«на языке
![]() »).
Пусть а
и А
— конечные числа. Число А
называется пределом функции
»).
Пусть а
и А
— конечные числа. Число А
называется пределом функции
![]() при
при
![]() ,
если для любого, сколь угодно малого,
числа
,
если для любого, сколь угодно малого,
числа
![]() можно указать число
можно указать число
![]() такое, что как только
такое, что как только
![]() и
и
![]() ,
так сейчас же
,
так сейчас же
![]() .
.
Множество значений
аргумента х
из X,
удовлетворяющих условиям:
![]() и
и
![]() будем называть проколотой
будем называть проколотой
![]() -окрестностью
точки а и обозначать через
-окрестностью
точки а и обозначать через
![]() .
.
Сущность соотношения
![]() состоит в следующем: значения функции
состоит в следующем: значения функции
![]() должны содержаться в любой, сколь угодно
малой, наперед заданной
должны содержаться в любой, сколь угодно
малой, наперед заданной
![]() -окрестности
предела А,
как только значения независимой
переменной оказываются лежащими в
надлежащим образом выбранной проколотой
-окрестности
предела А,
как только значения независимой
переменной оказываются лежащими в
надлежащим образом выбранной проколотой
![]() -окрестности
точки а
(
-окрестности
точки а
(![]() зависит от
зависит от
![]() ).
).
Замечание 1.
Определения 1 и 2 предела функции
![]() при
при
![]() равносильны. Это можно доказать.
равносильны. Это можно доказать.
Замечание 2.
В определении предела функции
![]() при
при
![]() у нас a
и А
были конечными числами. Отметим, что a
и А
могут быть и символами (несобственными
числами):
у нас a
и А
были конечными числами. Отметим, что a
и А
могут быть и символами (несобственными
числами):
![]() .
Если либо а,
либо А
(либо а
и А
оба сразу) — несобственные числа, то
определение предела функции
.
Если либо а,
либо А
(либо а
и А
оба сразу) — несобственные числа, то
определение предела функции
![]() (в зависимости оттого, какой случай
имеет место) будет следующим.
(в зависимости оттого, какой случай
имеет место) будет следующим.
1.
Пусть
![]() — конечное число.
— конечное число.
Число А
называется конечным
пределом функции
![]() при
при
![]() ,
если для любого, сколь угодно малого
числа
,
если для любого, сколь угодно малого
числа
![]() можно указать число
можно указать число
![]() такое, что как только
такое, что как только
![]() (
(![]() ),
так сейчас же
),
так сейчас же
![]() .
В этом случае пишут
.
В этом случае пишут
![]() .
.
2.
Пусть
![]() — конечное число.
— конечное число.
Число А
называется конечным
пределом функции
![]() при
при
![]() ,
если для любого, сколь угодно малого
числа
,
если для любого, сколь угодно малого
числа
![]() можно указать число
можно указать число
![]() такое, что как только
такое, что как только
![]() (
(![]() ),
так сейчас же
),
так сейчас же
![]() .
Запись:
.
Запись:
![]() .
.
3.
Пусть а
— конечное число;
![]() .
Говорят, что
.
Говорят, что
![]() при
при
![]() ,
и пишут
,
и пишут
![]() ,
если любому, как угодно большому, числу
М
> 0 отвечает число
,
если любому, как угодно большому, числу
М
> 0 отвечает число
![]() такое, что для всех
такое, что для всех
![]() (
(![]() )
имеет место неравенство:
)
имеет место неравенство:
![]() .
.
4.
Пусть а
— конечное число;
![]() .
Говорят, что
.
Говорят, что
![]() при
при
![]() ,
и пишут
,
и пишут
![]() ,
если любому, как угодно большому, числу
М
> 0 отвечает число
,
если любому, как угодно большому, числу
М
> 0 отвечает число
![]() такое, что для всех
такое, что для всех
![]() (
(![]() )
имеет место неравенство:
)
имеет место неравенство:
![]() .
.
5.
Пусть
![]() .
Говорят, что
.
Говорят, что
![]() при
при
![]() ,
и пишут
,
и пишут
![]() ,
если любому, как угодно большому, числу
М
> 0 отвечает число
,
если любому, как угодно большому, числу
М
> 0 отвечает число
![]() такое, что как только
такое, что как только
![]() (
(![]() ),
так сейчас же
),
так сейчас же
![]() .
.
6.
Пусть
![]() .
Говорят, что
.
Говорят, что
![]() при
при
![]() ,
и пишут
,
и пишут
![]() ,
если любому, как угодно большому, числу
М
> 0 отвечает число
,
если любому, как угодно большому, числу
М
> 0 отвечает число
![]() такое, что как только
такое, что как только
![]() (
(![]() ),
так сейчас же
),
так сейчас же
![]() .
.
7.
Пусть
![]() .
Говорят, что
.
Говорят, что
![]() при
при
![]() ,
и пишут
,
и пишут
![]() ,
если любому, как угодно большому, числу
М
> 0 отвечает число
,
если любому, как угодно большому, числу
М
> 0 отвечает число
![]() такое, что как только
такое, что как только
![]() (
(![]() ),
так сейчас же
),
так сейчас же
![]() .
.
8.
Пусть
![]() .
Говорят, что
.
Говорят, что
![]() при
при
![]() ,
и пишут
,
и пишут
![]() ,
если любому, как угодно большому, числу
М
> 0 отвечает число
,
если любому, как угодно большому, числу
М
> 0 отвечает число
![]() такое, что как только
такое, что как только
![]() (
(![]() ),
так сейчас же
),
так сейчас же
![]() .
.
