Капиллярные явления. Смачивание и несмачивание

При соприкосновении жидкости с твердым телом наблюдается смачивание или несмачивание этого тела жидкостью. Будет ли данная жидкость смачивать твердое тело или нет, зависит от взаимодействия молекул жидкости, твердого тела и газа, с которым граничат поверхности этого тела и жидкости.

К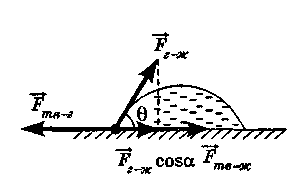огда жидкость смачивает поверхность твердого тела, то она растекается по ней, а когда не смачивает, то стягивается на этой поверхности в каплю. Явления смачивания или несмачивания определяются величинами поверхностного натяжения между жидкостью и твердым телом, жидкостью и газом и твердым телом и газом. Рассмотрим рисунок. Пусть капля на поверхности твердого тела находится в равновесии. Так будет, когда все силы поверхностного натяжения, приложенные к некоторому малому элементу контура, ограничивающего каплю, уравновешены. На элемент контура действуют: сила поверхностного натяжения , приложенная к элементу на границе твердое тело-газ, сила поверхностного натяжения , приложенная к этому элементу на границе твердое тело-жидкость, и составляющая силы F_г-ж, приложенной к нему на границе жидкость-газ. Условие равновесия будет , когда , откуда . Здесь  - краевой угол, т. е. угол между касательными к поверхностям твердого тела и жидкости, отсчитываемый через жидкость. Поскольку cos всегда меньше или равен 1, равновесие может наблюдаться только тогда, когда . Случай  = 0 называют полным смачиванием,  = 180 - полным несмачиванием. При смачивании краевой угол острый, при несмачивании – тупой.

Капиллярные явления. Дополнительное давление над искривленной поверхностью

Узкие трубки, диаметр которых во много раз меньше их длины, называют капиллярами.

Если капилляр опустить в жидкость, которая смачивает его поверхность, то жидкость поднимется по капилляру и ее верхний уровень в капилляре расположится выше уровня жидкости в сосуде. Если капилляр опустить в жидкость, которая не смачивает его поверхность, то она, наоборот, опустится по капилляру так, что ее верхний уровень в капилляре расположится ниже ее уровня в сосуде. Явления подъема жидкости по капилляру при смачивании и опускания при несмачивании называются капиллярными явлениями. Капиллярные явления обусловлены силами поверхностного натяжения и искривлением поверхности жидкости. Такое искривление называется мениском. При смачивании мениск вогнутый, а при несмачивании выпуклый. При полном смачивании мениск имеет форму вогнутой полусферы, а при полном несмачиваниивыпуклой полусферы.

Жидкость в капилляре находится в равновесии, если вес столба жидкости уравновешен силой поверхностного натяжения. , т.к. . Высота подъема жидкости в капилляре прямо пропорциональна ее поверхностному натяжению и обратно пропорциональна плотности жидкости и радиусу капилляра.

Т.к. давление на одном уровне в однородной жидкости одинаково, то для жидкости в капилляре и в сосуде должно выполняться условие: - давление над вогнутой поверхностью меньше атмосферного. Соответственно давление над выпуклой поверхностью больше атмосферного. Величину называют добавочным давлением Лапласа.