
- •Данель в.В.
- •Содержание 2
- •1. Плоская система сходящихся сил.
- •1.1. Сила-вектор
- •1.2. Сложение двух сил, сходящихся в одной точке.
- •1.3 Сложение нескольких сил, сходящихся в одной точке.
- •1.4 Равновесие системы сходящихся сил.
- •2. Плоская система произвольно расположенных сил.
- •2.1. Момент силы относительно точки.
- •2.2. Момент пары сил.
- •2.3. Главный вектор. Главный момент.
- •2.4. Влияние изменения центра приведения.
- •2.5. Равновесие твёрдого тела под действием плоской системы сил.
- •2.6. Типы опор.
- •2.7. Определение опорных реакций для простейших балок.
- •3. Анализ расчётных схем.
- •3.1. Переход от реальных сооружений к расчётным схемам.
- •3.2. Узлы стержневых систем.
- •3.2.1. Жёсткие узлы (рис.3.4).
- •3.2.2. Шарнирные узлы (рис3.5).
- •3.2.3. Упругие узлы (рис.3.6).
- •3.3. Чем опасна мгновенная изменяемость.
- •3.4. Принципы образования мгновенно и геометрически неизменяемых систем.
- •3.5. Степени свободы. Статическая определимость.
- •4. Виды стержневых систем.
- •4.1. Балки.
- •4.2. Рамы.
- •4.3. Фермы.
- •4.3.1 Элементы ферм.
- •4.3.2. Работа ферм.
- •5. Аналитические методы определения усилий в плоских статически определимых фермах. Рекомендации по конструированию.
- •5.1 Метод вырезания узлов
- •5.2. Метод моментных точек.
- •5.3. Метод проекций.
- •5.4. Рекомендации по конструированию ферм.
- •Подбор сечений растянутых элементов.
- •Подбор сечений сжатых элементов
- •Задание № 1.
- •Задание № 2
- •Темы рефератов по дисциплине «основы проектирования»
2.4. Влияние изменения центра приведения.
Главный момент изменяется с изменением центра приведения.
Зависимость главного момента от выбора центра приведения:
![]() ,
,
где
О и ![]() -два
разных центра приведения.
-два
разных центра приведения.
1)Т.к.
сила ![]() и пара с моментом
и пара с моментом ![]() лежат в одной плоскости, их можно привести
к одной силе
лежат в одной плоскости, их можно привести
к одной силе ![]() ,
приложенной в некоторой точке
,
приложенной в некоторой точке ![]() .Эта сила
.Эта сила ![]() является равнодействующей данной
плоской системы сил.
является равнодействующей данной
плоской системы сил.
ТЕОРЕМА
ВАРИНЬОНА. Если R≠0,![]() ,то
система сил приводится к одной
равнодействующей, не проходящей через
центр приведения О. При этом момент
равнодействующей относительно любой
точки будет равен алгебраической сумме
моментов всех данных сил относительно
той же точки.
,то
система сил приводится к одной
равнодействующей, не проходящей через
центр приведения О. При этом момент
равнодействующей относительно любой
точки будет равен алгебраической сумме
моментов всех данных сил относительно
той же точки.
Если
начало координат выбрано в центре
приведения и известны проекции ![]() всех сил на оси координат и координаты
всех сил на оси координат и координаты
![]() точек их приложения, то момент
равнодействующей находят по формуле
точек их приложения, то момент
равнодействующей находят по формуле
![]()
2)
Если R≠0
, ![]() ,система
приводитя к равнодействующей
,система
приводитя к равнодействующей ![]() ,
проходящей через центр приведения О.
,
проходящей через центр приведения О.
3)Если
главный вектор равен нулю (R=0),
а главный момент отличен от нуля (![]() ),
данная система эквивалентна паре сил.
Причём главный момент этой системы
будет равен моменту этой пары
),
данная система эквивалентна паре сил.
Причём главный момент этой системы
будет равен моменту этой пары ![]() и не зависит в данном случае от центра
приведения ( от выбора точки О).
и не зависит в данном случае от центра
приведения ( от выбора точки О).
4)
Если R=0,
![]() ,
система сил находится в равновесии. О
равновесии плоской системы сил после
рассмотрения примера.
,
система сил находится в равновесии. О
равновесии плоской системы сил после
рассмотрения примера.
Пример.
Дана плоская система сил ![]() В таблице 1.1. приведены проекции
В таблице 1.1. приведены проекции![]() этих сил на координатные оси, координаты
(
этих сил на координатные оси, координаты
( ![]() )
точек их приложения.
)
точек их приложения.
Привести эту систему к началу координат. Найти линию действия равнодействующей.
Таблица 1.1
|
Проекции и координаты |
Силы |
|||
|
P1 |
P2 |
P3 |
||
|
Проекции |
X |
1 |
-2 |
3 |
|
Y |
4 |
1 |
-3 |
|
|
Коорди- наты |
x |
2 |
-2 |
3 |
|
y |
1 |
-1 |
-3 |
|
Решение.
Найдём проекции главного вектора заданной системы сил:
![]()
![]()
Равнодействующая
![]() .
.
Главный
момент 
Пусть
А (x,y)
– точка действия линии искомой
равнодействующей ![]()
![]()
![]()
![]()
Поэтому
![]() .
.
С другой стороны, по теореме Вариньона
![]()
Следовательно,
![]() ,
т.е.
,
т.е.![]() .
.
Это и есть уравнение лини действия равнодействующей.
2.5. Равновесие твёрдого тела под действием плоской системы сил.
Для
равновесия плоской системы сил,
приложенных к твёрдому телу и не
пересекающихся в одной точке, необходимо
и достаточно, чтобы главный вектор ![]() этих сил и их главный момент
этих сил и их главный момент ![]() относительно произвольной точки О,
лежащей в плоскости действия этих сил,
были равны нулю, т.е.
относительно произвольной точки О,
лежащей в плоскости действия этих сил,
были равны нулю, т.е.
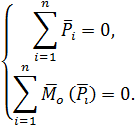
В проекциях на оси x и y:

Условия равновесия плоской системы сил, произвольно расположенных в плоскости, можно представить ещё в двух других видах.
1. Алгебраическая сумма моментов сил относительно трёх произвольных точек A,B,C, не лежащих на одной прямой, равна нулю, т.е.

2) Алгебраическая сумма моментов всех сил относительно трёх произвольных точек A и B равна нулю, и сумма проекций этих сил на какую-либо ось, не перпендикулярную прямой, соединяющий точки A и B, равна нулю, т.е.

В частном случае, когда все силы плоской системы параллельны, условия равновесия выражается двумя уравнениями вместо трёх (ось Ox параллельна данным силам):

Либо в виде

где прямая AB не параллельна данным силам.
Пример.
Балка
постоянного поперечного сечения весит
2000H
и имеет длину ![]() На
расстоянии
На
расстоянии ![]() от
правого торца приложена сила P=4000H
под углом
от
правого торца приложена сила P=4000H
под углом ![]() к горизонту. Определить усилия в тросах
1, 2 и 3 (рис. 2.4).
к горизонту. Определить усилия в тросах
1, 2 и 3 (рис. 2.4).

Рис. 2.4

Рис. 2.5.
Переходим
к расчётной схеме (рис. 2.5). Отбрасываем
подвески и заменяем их действия реакциями
![]() по направлению отброшенных связей. Вес
балки
по направлению отброшенных связей. Вес
балки ![]() сосредотачиваем в её середине . Оси x
и y
показаны на рисунке.
сосредотачиваем в её середине . Оси x
и y
показаны на рисунке.
Уравнение равновесия в проекции на ось x:

Здесь и далее уравнение равновесия будем составлять в такой последовательности, при которой в каждом уравнении будет только одно неизвестное усилие. Моментное уравнение равновесия относительно точки A:
![]() Pб
×АС
+ Р
×
Pб
×АС
+ Р
×![]() ×AD – N3×AB
= 0;
×AD – N3×AB
= 0;
2000×0,5×l
+ 4000×![]() - N3×l
= 0,
- N3×l
= 0,
N3= 2885,6 Н.
Моментное уравнение равновесия относительно точки B:
![]() N2
×АB
– Рб
×CB - P×
N2
×АB
– Рб
×CB - P× ![]() ×
×![]() = 0;
= 0;
N2×l
- 2000×0,5×l - 4000×![]() = 0;
= 0;
N2 = 1942,8 Н. Четвёртое уравнение равновесия используем для проверки правильности найденных реакций.
В проекции на ось y

Т.к.
это уравнение равновесия выполняется,
реакции ![]() и
и ![]() найдены правильно.
найдены правильно.
Ответ:![]() Все тросы растянуты.
Все тросы растянуты.
В рассмотренной системе число уравнений равновесия было достаточно для определения всех опорных реакций (статически определимая система).
