2.4.4. Другие методы

S: Для анализа индуктивно-связанных цепей рекомендуется применять метод …

+: контурных токов

-: узловых напряжений

-: переменных состояния

-: наложения

I:

S: Для анализа непланарных цепей рекомендуется применять метод …

-: контурных токов

+: узловых напряжений

-: переменных состояния

-: наложения

I:

S: В большинстве современных программ машинного анализа электронных схем применяется метод …

-: контурных токов

+: узловых напряжений

-: переменных состояния

-: наложения

I:

S: В качестве независимых переменных в методе токов ветвей используются …

+: токи ветвей

-: контурные токи

-: токи индуктивностей и напряжения ёмкостей

-: напряжения узлов

I:

S: В качестве независимых переменных в методе переменных состояния используются …

-: токи ветвей

-: контурные токи

+: токи индуктивностей и напряжения ёмкостей

-: напряжения узлов

I:

S: Обобщённая ветвь электрической цепи описывается уравнением

+:

-:

-:

-:

I:

S: Параметры эквивалентного источника ЭДС

+:

-:

-:

-:

I:

S: Наименьшее количество уравнений, необходимое для анализа данной цепи, даёт метод

+: узловых напряжений

-: контурных токов

-: токов ветвей

-: напряжений ветвей

2.5. Анализ цепей со связанными индуктивностями

2.5.1. Формирование уравнений с учётом индуктивных связей

S: Цепи, в которых наводятся ЭДС взаимной индукции, называются…

+: индуктивно связанными

-: взаимными

-: трансформаторы

-: реактивными

I:

S: В соответствии с законом электромагнитной индукции ЭДС взаимной индукции равна …

+:

-:

-:

-:

I:

S: Индуктивные катушки, изображённые на рисунке, включены

+: встречно

-: согласно

-: параллельно

-: независимо

I:

S: Индуктивные катушки, изображённые на рисунке, включены

+: согласно

-: встречно

-: параллельно

-: независимо

I:

S: Уравнения электрического равновесия:

+:

-:

-:

-:

I:

S: Уравнения электрического равновесия:

i₁

i₂

+:

-:

-:

-:

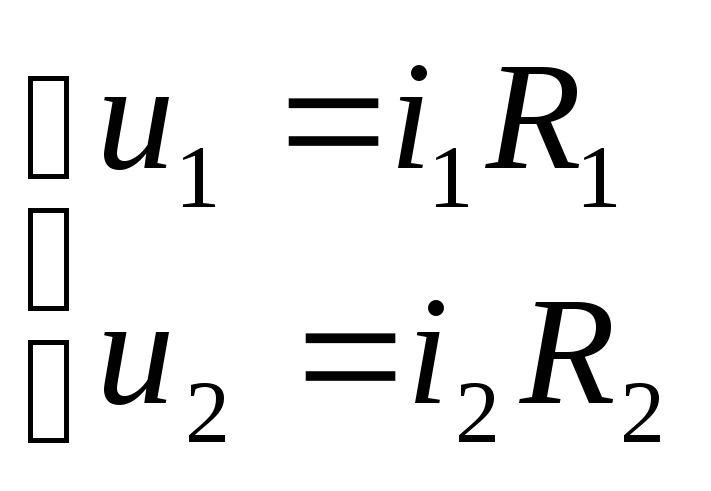
I:

S: Коэффициент связи между катушками

+:

-:

-:

-:

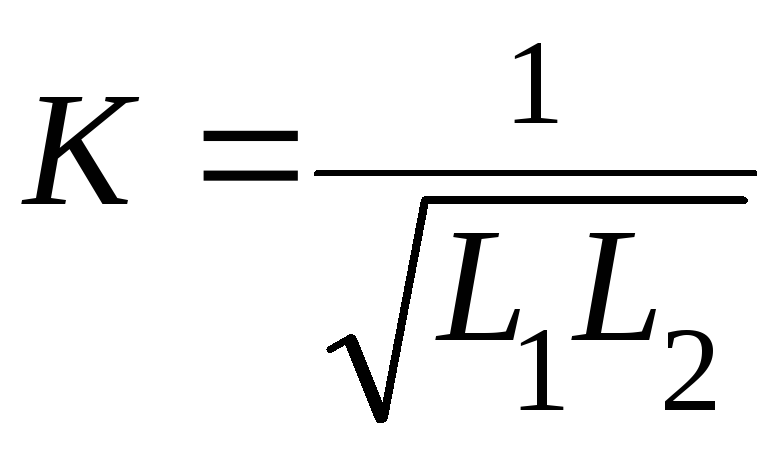
I:

S: Коэффициент связи между катушками изменяется в пределах …

+: 0…1

-: 1…

-: -1…1

-:-…

I:

S: Взаимная индуктивность может изменяться в пределах …

-: 0…1

+: 0…

-: -1…1

-:-…

I:

S: Взаимная индуктивность не связанных катушек равна

+: 0

+: 1

-: -1

-:-

I:

2.5.2. Связанные индуктивности при гармоническом воздействии

I:

S: Сопротивление связи индуктивных катушек …

+: Z_M = jM

-: Z_M = jwL

-: Z_M = R

-: Z_M = L

I:

S: Компонентные уравнения связанных индуктивностей в комплексной форме:

+:

-:

-:

-:

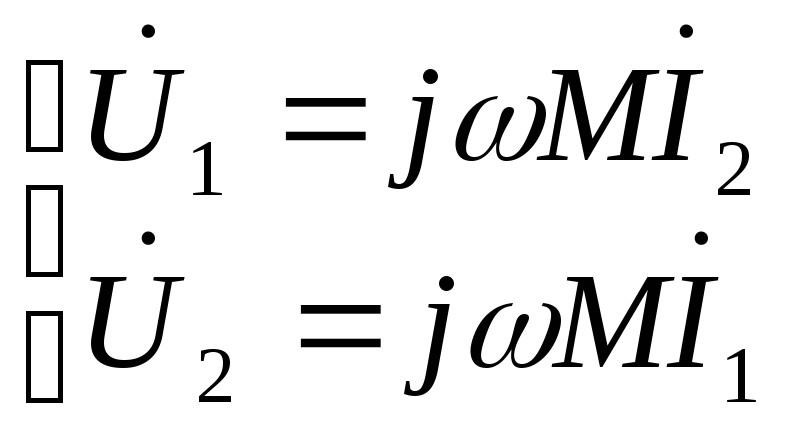
I:

S: Эквивалентное сопротивление двух последовательно соединённых связанных индуктивностей, включенных встречно, …

+: Z = j (L₁ + L₂ - 2M)

-: Z = j (L₁ + L₂ + M)

-: Z = jL₁ + jL₂

-: Z = R₁ + R₂

I:

S: Эквивалентное сопротивление двух последовательно соединённых связанных индуктивностей, включённых согласно…

+: Z = j (L₁ + L₂ + 2M)

-: Z = j (L₁ + L₂ + M)

-: Z = jL₁ + jL₂

-: Z = R₁ + R₂

I:

S: Для анализа сложных цепей со связанными индуктивностями рекомендуется применять …

+: метод контурных токов

-: метод узловых напряжений

-: метод эквивалентного генератора

-: метод наложения

I:

S: При замене связанных индуктивностей эквивалентной схемой без индуктивных связей

L_1Э

L_2Э

L₃

+: L_1Э = L₁ + M, L_2Э = L₂ + M, L₃ = M

-: L_1Э = L₁, L_2Э = L₂, L₃ = M

-: L_1Э = L₁ + 2M, L_2Э = L₂ + 2M, L₃ = 2M

-: L_1Э = M, L_2Э = M, L₃ = M

I:

S: Эквивалентная индуктивность равна ### мГн при L₁ = L₂ = 5 мГн, М = 2 мГн

+: 14

I:

S: Эквивалентная индуктивность равна ### мГн при L₁ = L₂ = 5 мГн, М = 2 мГн

+: 6

I:

S: Сопротивление связи индуктивных катушек зависит от…

+: частоты

+: взаимной индуктивности

-: индуктивности катушек

-: протекающего через катушки тока

I:

S: Уравнение электрического равновесия цепи

+:

-:

-:

-:

*

L₁

М

R₁

*

L₂

R₂

I: