Теоремы об изменении количества движения и кинетического момента при ударе.

Как указывалось в главе ………, теорема об изменении главного вектора количества движения имела вид

_{, (3.79)}

где - главный вектор внешних сил, действующих на систему. Умножим обе части формулы (3.79) на и проинтегрируем обе части, получим

,

здесь -главный импульс внешних сил. Вспоминая также, что

,

получаем окончательную формулу изменения главного вектора количества движения при ударе

(3.80)

Теорема об изменении главного вектора момента количества движения или кинетического момента имела вид

. (3.81)

Так же как и выше умножим обе части формулы (3.81) на 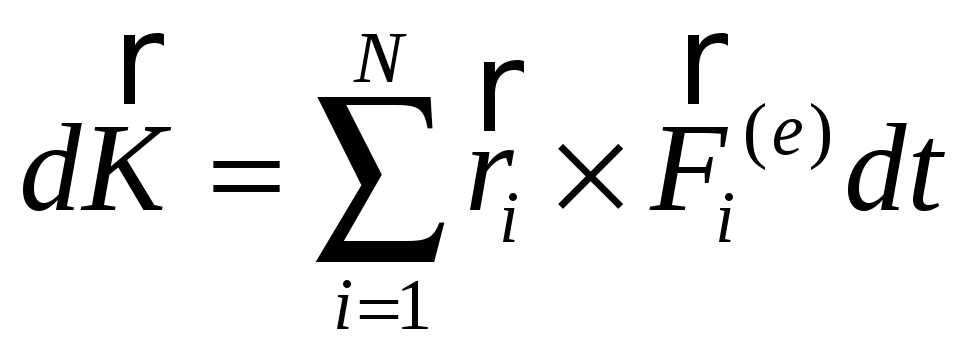и проинтегрируем обе части, получим

, (3.82)

где - главный момент импульсов внешних сил.

Запишем уравнения (3.81) в проекциях на оси координат. Для твердого тела в качестве осей координат удоб­нее выбрать оси, жестко связанные с телом; начало координат­ной системы следует выбрать либо в неподвижной точке О тела (если такая точка существует) либо в его центре масс С. Следует отметить, что при ударе все точки системы, в частности, твердого тела, не перемещаются. Поэтому можно выбрать лю­бую систему координатных осей, жестко связанных с телом и заменить векторные уравнения (3.81) тремя ска­лярными уравнениями (см. §………):

(3.83)

В этих уравнениях и — проекции вектора угловой скорости тела в начале и конце удара, — соответствующие моменты инерции тела, — проекции главного момента импульсов внешних ударных сил. Если за оси координат приняты главные оси инерции тела, то уравнения (3.83) примут такой вид:

.

Удар, действующий на тело, вращающегося вокруг неподвижной оси.

На тело, закрепленное в точке В шарнирно (рис.) и в точке А при помощи подпятника, действует ударный им­пульс . Во время удара в точках А и В возникают реакции, имеющие также характер ударных сил. При значительных ударных воздействиях реакции могут достигать значений, опас­ных с точки зрения прочности подшип­ников и оси. Возникает задача определения удар­ных импульсов реакций при заданных динамических характеристиках тела (масса, моменты инерции) и при извест­ном ударном импульсе, действующем на тело.

Пусть — ударный импульс, дей­ствующий в точке М на тело. Совместим плоскость уАz с плоскостью, проходящей через центр масс С тела. Теорема об из­менении количества движения при ударе и теорема об измене­нии момента количеств движения примут для нашего случая следующий вид:

(3.84)

(3.85)

где и — импульсы реакций, а — радиус-вектор точки М.

Заметим, что скорость центра масс параллельна оси х

и, следовательно, векторное уравнение (3.84) в проекциях на оси координат приводит к трем скалярным уравнениям:

(3.86)

Здесь — проекции ударных импульсов на соответствующие оси координат.

Теперь перейдем к составлению второй группы уравнений, вытекающей из векторного равенства (3.85). В проекции на оси координат эти уравнения в общем виде совпадают с урав­нениями (3.83). Для того чтобы воспользоваться этими урав­нениями, вычислим, прежде всего, момент ударного импульса. Имеем:

Где и — координаты точки М приложения им­пульса .

Уравнения (3.83) принимают следующий вид:

(3.87)

Из последнего уравнения определяется приращение угловой скорости вращения за время удара:

Для определения неизвестных импульсов ударных сил остается подставить в левые части уравнений (3.86) и (3.87) и решить систему пяти уравнений с пятью неизвестными .