Вариант 1.

Тема: «Дифференциальное исчисление

функции одной переменной»

1. Найти производные первого порядка:

1) ; 3) ; 5) ;

2) ; 4) ; 6) .

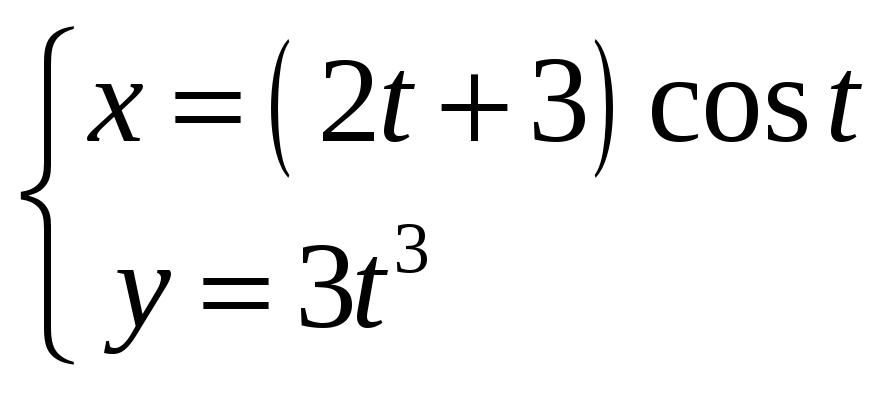2. Дана функция .

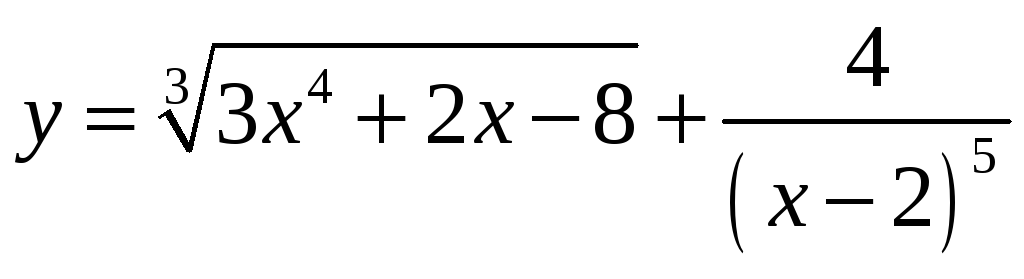а) Найти дифференциал первого порядка в общем виде.

б) Записать уравнение касательной и нормали к данной кривой в точке с абсциссой .

3. Для функции и аргумента вычислить .

4. Найти указанные пределы, используя правило Лопиталя:

1) ; 2) ; 3) .

5. Найти наименьшее и наибольшее значения функции на отрезке .

6. Провести полное исследование функции и построить ее график:

1) ; 2) .

Тема: «Приложения производной функции»

1. Закон движения тела имеет вид: (м). Найти:

1) скорость и ускорение движения тела в момент время с;

2) кинетическую энергию тела через с после начала движения, если его масса кг (ответ записать в кДж).

2. Измерения величины заряда (в микрокулонах) на обкладках конденсатора показали, что заряд меняется со временем по закону . Найти, в какой момент времени (время в секундах, ) сила тока будет равна нулю.

3. Полотняный шатер объемом куб.ед. имеет форму прямого конуса. Каково должно быть отношение высоты конуса к радиусу его основания, чтобы на шатер пошло наименьшее количество полотна?

Вариант 2.

Тема: «Дифференциальное исчисление

функции одной переменной»

1. Найти производные первого порядка:

1) ; 3) ; 5) ;

2) ; 4) ; 6) .

2. Дана функция .

а) Найти дифференциал первого порядка в общем виде.

б) Записать уравнение касательной и нормали к данной кривой в точке с абсциссой .

3. Для функции и аргумента вычислить .

4. Найти указанные пределы, используя правило Лопиталя:

1) 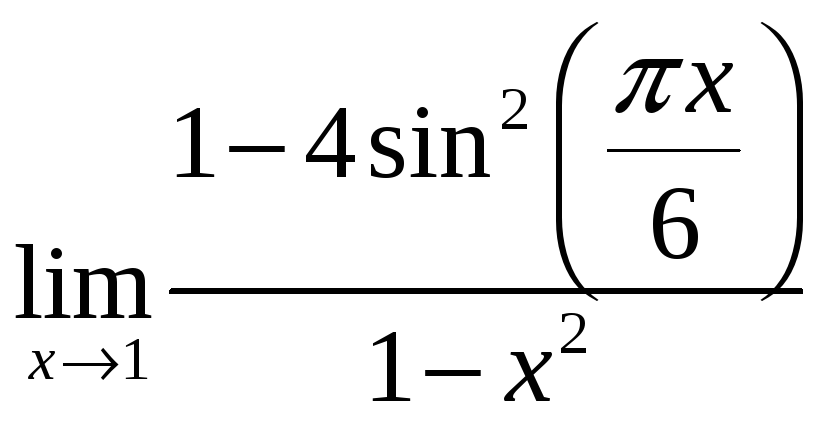; 2) 3) .

5. Найти наименьшее и наибольшее значения функции на отрезке .

6. Провести полное исследование функции и построить ее график:

1) ; 2) .

Тема: «Приложения производной функции»

1. Закон движения тела имеет вид: (м). Найти:

1) скорость и ускорение движения тела в момент время с;

2) кинетическую энергию тела через с после начала движения, если его масса кг (ответ записать в кДж).

2. Измерения величины заряда (в микрокулонах) на обкладках конденсатора показали, что заряд меняется со временем по закону . Найти, в какой момент времени (время в секундах, ) сила тока будет равна нулю.

3. Требуется сделать коническую воронку с образующей, равной 20 см. Какой должна быть высота воронки, чтобы ее объем был наибольшим?

Вариант 3.

Тема: «Дифференциальное исчисление

функции одной переменной»

1. Найти производные первого порядка:

1) ; 3) ; 5) ;

2) ; 4) ; 6) .

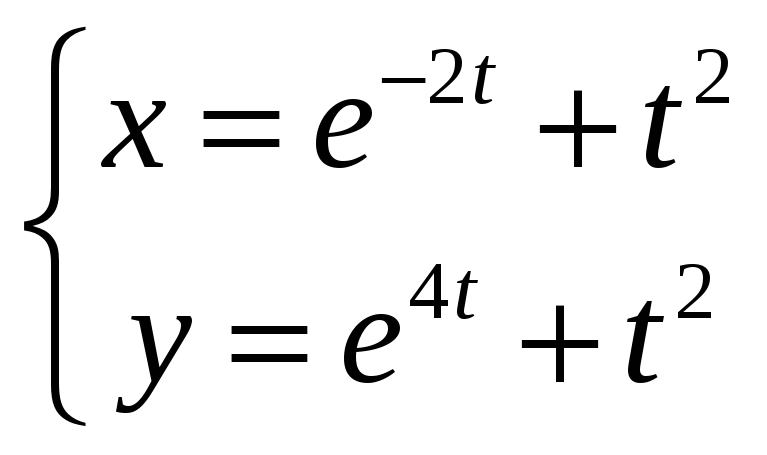2. Дана функция .

а) Найти дифференциал первого порядка в общем виде.

б) Записать уравнение касательной и нормали к данной кривой в точке с абсциссой .

3. Для функции и аргумента вычислить .

4. Найти указанные пределы, используя правило Лопиталя:

1) ; 2) ; 3) .

5. Найти наименьшее и наибольшее значения функции на отрезке .

6. Провести полное исследование функции и построить ее график:

1) ; 2) .

Тема: «Приложения производной функции»

1. Закон движения тела имеет вид: (м). Найти:

1) скорость и ускорение движения тела в момент время с;

2) кинетическую энергию тела через с после начала движения, если его масса кг (ответ записать в кДж).

2. Измерения величины заряда (в микрокулонах) на обкладках конденсатора показали, что заряд меняется со временем по закону . Найти, в какой момент времени (время в секундах, ) сила тока будет равна нулю.

3. Проволокой, длина которой м, необходимо огородить клумбу, имеющую форму кругового сектора. Каким должен быть радиус круга, чтобы площадь клумбы была наибольшей?