
- •Часть 2
- •Часть 2
- •1. Механические колебания
- •Уравнение гармонических колебаний
- •2. Механические волны
- •3. Электромагнитные колебания. Переменный ток. Электромагнитные волны
- •4. Уравнения максвелла
- •5. Шкала электромагнитных волн
- •6. Геометрическая оптика
- •7. Интерференция света
- •8. Дифракция света
- •9. Поляризация света
- •10. Дисперсия света
- •11. Квантовая природа излучения
- •12. Элементы квантовой физики атомов, молекул и твердых тел
- •12.1. Теория атома водорода по Бору
- •12.2. Элементы квантовой механики
- •12.3. Квантовые свойства атомов, молекул и твердых тел
- •13. Элементы физики атомного ядра и элементарных частиц
- •13.1. Элементы физики атомного ядра
- •13.2. Элементарные частицы Классификация элементарных частиц
- •Типы взаимодействия элементарных частиц
- •14. Выдержки из демонстрационного варианта по физике сайта федерального интернет-экзамена в сфере профессионального образования (www.Fepo.Ru)
- •15. Правильные ответы
- •Содержание
- •Механические колебания …………………………… 6
- •Часть 2 колебания, волны, оптика, атомная и ядерная физика
СПРАВОЧНОЕ РУКОВОДСТВО ПО ФИЗИКЕ
Часть 2
Колебания, волны, оптика,
атомная и ядерная физика
Ростов-на-Дону 2009
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
СПРАВОЧНОЕ РУКОВОДСТВО ПО ФИЗИКЕ
Часть 2
Колебания, волны, оптика,
атомная и ядерная физика
Учебное пособие
Ростов-на-Дону 2009
УДК 530.1
С 74
Авторы: Егоров И.Н., Егорова С.И., Кунаков В.С., Лемешко Г.Ф., Наследников Ю.М.
С 74 Справочное руководство по физике. Ч.2. колебания, волны, оптика, атомная и ядерная физика: Учеб. пособие. - Ростов н/Д: Издательский центр ДГТУ, 2009. – 49 с.
Цель пособия – помощь студентам в самостоятельной работе при решении задач, подготовке к экзаменам, а также при подготовке к Интернет-тестированию.
Предназначено для студентов всех специальностей очной, заочной и ускоренной форм обучения
Печатается по решению редакционно-издательского совета
Донского государственного технического университета
Научный редактор: д-р техн.наук, проф. В.С. Кунаков
Егоров И.Н., Егорова С.И.,
Кунаков В.С., Лемешко Г.Ф.,
Наследников Ю.М.
2009
Издательский центр ДГТУ
1. Механические колебания
-
Уравнение гармонических колебаний
![]() ,
,
где
![]() –
смещение точки от положения равновесия,
А
–
амплитуда колебаний,
–
смещение точки от положения равновесия,
А
–
амплитуда колебаний,![]() -
фаза колебаний, 0–
круговая (циклическая частота), t
– время,
-
фаза колебаний, 0–
круговая (циклическая частота), t
– время,
![]() – начальная фаза колебаний.
– начальная фаза колебаний.
![]() ,
,
где
![]() –
частота колебаний,
–
частота колебаний,
![]() –
период колебаний.
–
период колебаний.
-
Скорость и ускорение при гармонических колебаниях
![]() ,
,
![]() -
амплитуда скорости (максимальное
значение);
-
амплитуда скорости (максимальное
значение);
![]() ,
,
![]() -
амплитуда ускорения (максимальное
значение).
-
амплитуда ускорения (максимальное
значение).
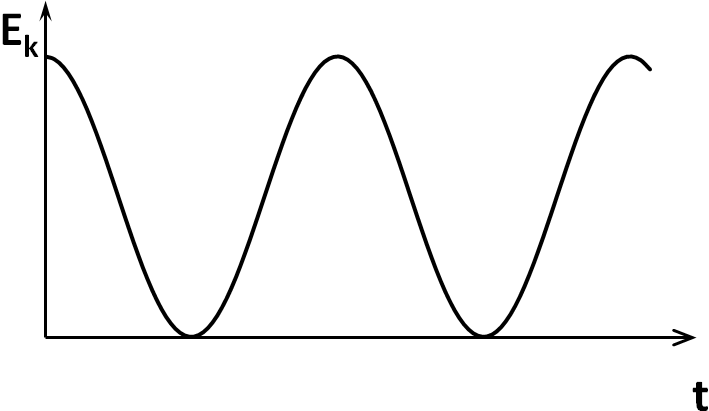
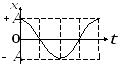
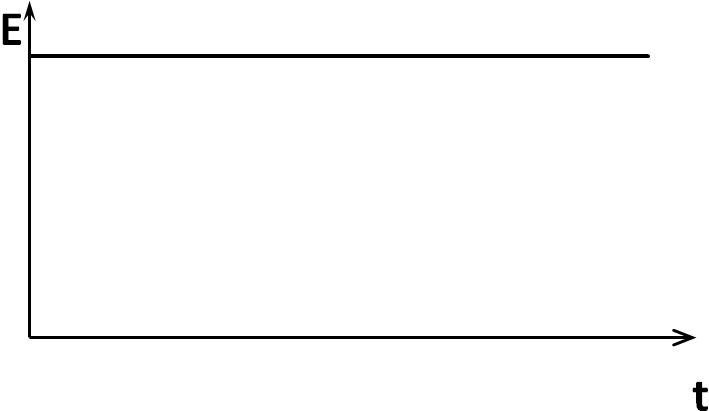
При
![]() графики зависимостей
графики зависимостей
![]() представлены на рис. 1(а,б,в), соответственно.
представлены на рис. 1(а,б,в), соответственно.
-
Возвращающая сила
![]() ,
,
где
![]() –
коэффициент упругой (квазиупругой)
силы, m
– масса материальной точки;
–
коэффициент упругой (квазиупругой)
силы, m
– масса материальной точки;
![]() -
амплитуда силы (максимальное значение).
-
амплитуда силы (максимальное значение).
-
Кинетическая энергия колеблющейся точки
![]()
![]() -амплитуда
кинетической энергии (максимальное
значение).
-амплитуда
кинетической энергии (максимальное
значение).![]()
а а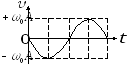
б б
в в
Рис. 1 Рис. 2
-
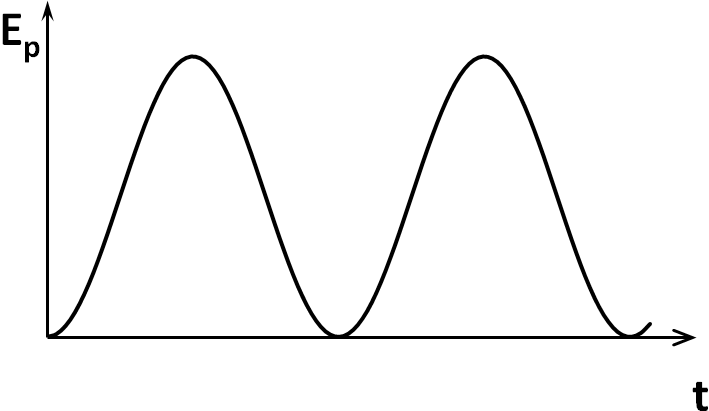
Потенциальная энергия колеблющейся точки
![]()
![]() -амплитуда
потенциальной энергии (максимальное
значение).
-амплитуда
потенциальной энергии (максимальное
значение).
При
![]() графики зависимостей кинетической и
потенциальной энергии от времени
представлены на рис. 2а и 2б, соответственно.
графики зависимостей кинетической и
потенциальной энергии от времени
представлены на рис. 2а и 2б, соответственно.
-
Полная энергия при гармонических колебаниях (рис. 2в)
![]() .
.
-
Уравнения гармонических колебаний могут быть заданы функциями синуса или косинуса. В таблице 1 даны значения скорости, ускорения, силы и энергии в обоих случаях.
Таблица 1
|
|
|
-
Периоды колебаний:
![]() –
математический
маятник (
–
математический
маятник (![]() –
длина нити);
–
длина нити);
![]() –
пружинный
маятник (m
– масса тела,
–
пружинный
маятник (m
– масса тела,
![]() –
коэффициент жесткости);
–
коэффициент жесткости);
![]() – физический
маятник (
– физический
маятник (![]() –
момент инерции тела относительно оси,
проходящей через точку подвеса,
определяется по теореме Штейнера, m
–
масса тела,
d
–
расстояние от точки подвеса до центра
масс).
–
момент инерции тела относительно оси,
проходящей через точку подвеса,
определяется по теореме Штейнера, m
–
масса тела,
d
–
расстояние от точки подвеса до центра
масс).
Пример:
Однородный диск радиусом
![]() колеблется около горизонтальной оси,
проходящей на расстоянии
колеблется около горизонтальной оси,
проходящей на расстоянии
![]() от центра диска. Определить период
от центра диска. Определить период
![]() колебаний диска относительно этой оси
(рис. 3).
колебаний диска относительно этой оси
(рис. 3).
П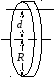 ериод
определяется по формуле
ериод
определяется по формуле
![]() ,
где
,
где
![]()
![]()
![]() (нашли
по теореме Штейнера). Тогда
(нашли
по теореме Штейнера). Тогда
![]() Рис.
3
Рис.
3
-
Уравнение затухающих колебаний (рис. 4)
![]() ,
,
где
![]() –
амплитуда колебаний в начальный момент
времени,
–
амплитуда колебаний в начальный момент
времени,![]() –
коэффициент затухания,
–
коэффициент затухания,
![]() -
зависимость амплитуды затухающих
колебаний от времени,
-
зависимость амплитуды затухающих
колебаний от времени,
![]() -частота
затухающих колебаний,
-частота
затухающих колебаний,
![]() -
частота собственных колебаний,
-
частота собственных колебаний,
![]() -
период затухающих колебаний.
-
период затухающих колебаний.

-
Уравнение вынужденных колебаний, совершаемых под действием периодически изменяющейся силы
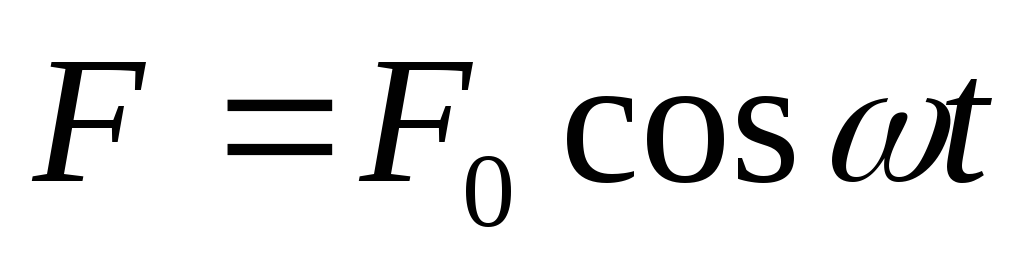
![]() ,
где
,
где
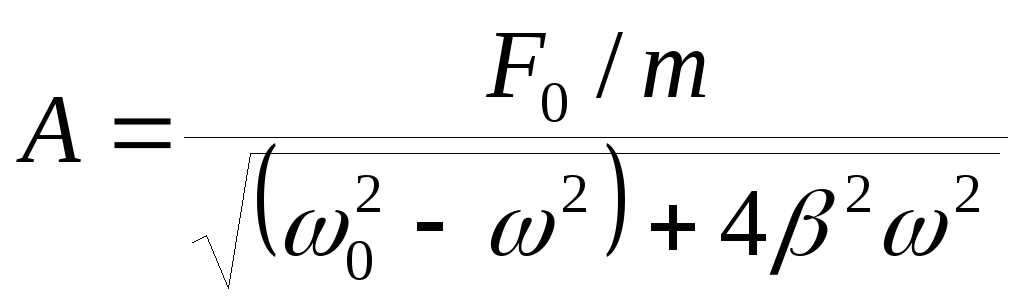 -
амплитуда вынужденных колебаний;
-
амплитуда вынужденных колебаний;
![]() -
начальная фаза вынужденных колебаний;
-
начальная фаза вынужденных колебаний;
![]() и
и
![]() -
частоты собственных и вынужденных
колебаний .
-
частоты собственных и вынужденных
колебаний .
-
Резонанс – резкое возрастание амплитуды вынужденных колебаний при частоте, близкой к частоте собственных колебаний.
-
Амплитуда при резонансе
![]() .
.
-
Резонансная частота
![]() .
.
Дифференциальные уравнения колебаний
![]() -
гармонические,
-
гармонические,
![]() -
затухающие,
-
затухающие,
![]() -
вынужденные.
-
вынужденные.
-
Уравнение колебания, полученного при сложении двух колебаний одинаковой частоты и одного направления, амплитуды колебаний которых
 и
и
 ,
а начальные фазы
,
а начальные фазы
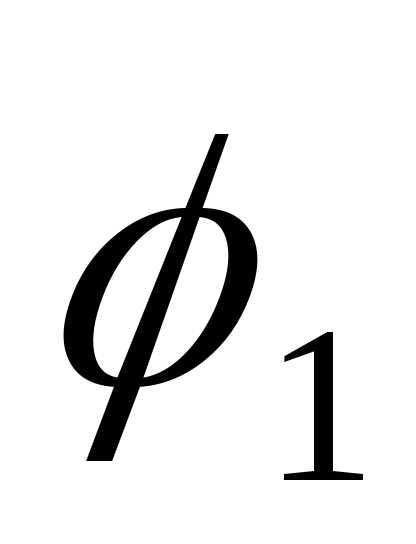 и
и
 ,
,
![]() ,
где
,
где
![]() -
-
амплитуда
результирующего колебания,
![]() - разность фаз слагаемых колебаний;
начальная фаза результирующего колебания
определяется формулой
- разность фаз слагаемых колебаний;
начальная фаза результирующего колебания
определяется формулой
![]() .
.
-
Уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях с одинаковыми частотами
![]() :
:
а)
если
![]() ,
то
,
то
![]() - уравнение прямой,
- уравнение прямой,
б)
если
![]() ,
то
,
то
![]() - уравнение прямой,
- уравнение прямой,
в)
если
![]() ,
то
,
то
![]() - уравнение эллипса, приведённого к
осям,
- уравнение эллипса, приведённого к
осям,
г)
если
![]() и
и
![]() ,
то
,
то
![]() - уравнение окружности, где
- уравнение окружности, где
![]() -
радиус окружности.
-
радиус окружности.
