1.1.3. Момент силы относительно точки и оси. Пара сил

Момент силы относительно центра. Опыт показывает, что эффект действия силы, приложенной к телу (например, к рычагу, штурвалу) на разных расстояниях от точки закрепления тела, зависит от так называемого м о м е н

т а с и л ы относительно точки закрепления.

Моментом силы относительно центра О называется произведение модуля силы на кратчайшее расстояние от центра О до линии действия силы.

M_о() = ± Fh, (1.6)

где h - кратчайшее расстояние от центра О до линии действия силы .

Момент силы считается положительным, если сила стремится повернуть тело вокруг центра О против хода часовой стрелки и отрицательным, если по ходу часовой стрелки (рис. 1.24, 1.25). Размерность момента силы Н·м.

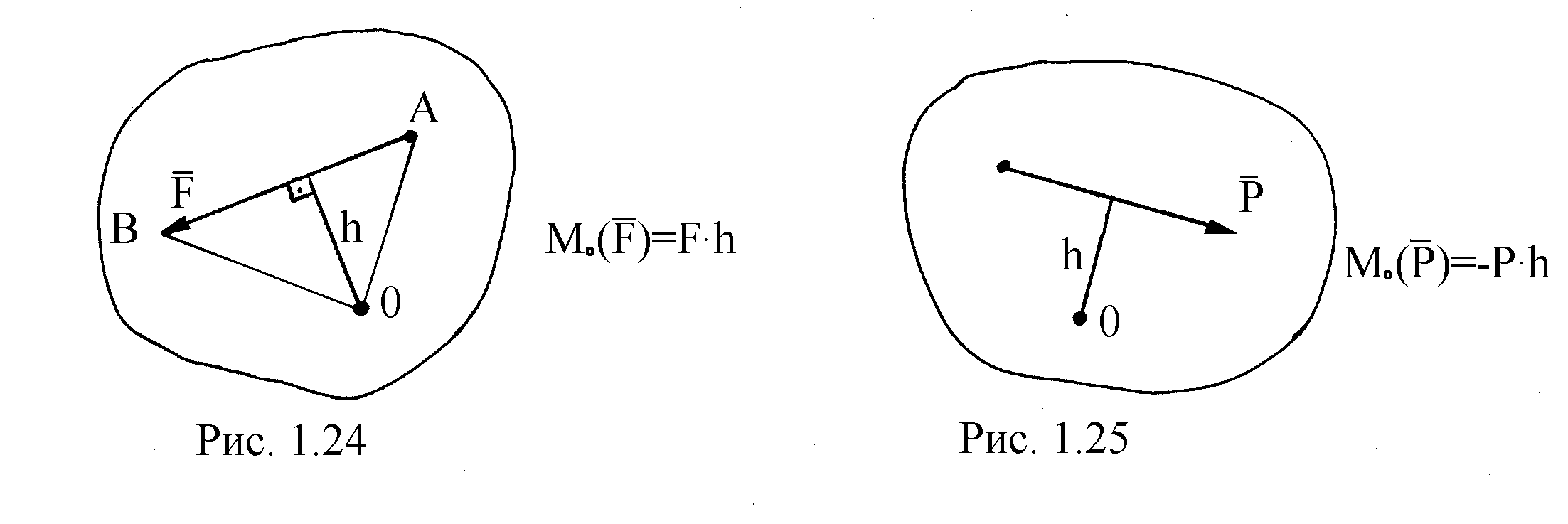Рис. 1.24 Рис. 1.25

Момент силы не изменяется при переносе точки приложения силы вдоль ее линии действия. Момент силы относительно центра О равен нулю, если сила равна нулю или, если линия действия силы проходит через центр О (плечо равно нулю).

Графически абсолютная величина момента силы относительно центра О выражается удвоенной площадью Δ ОАВ

M_o () = 2S ∆ ОАВ (1.7)

Момент силы относительно центра как векторное произведение. Введенного понятия "момент силы относительно центра как алгебраическая величина" оказывается недостаточно в случае сил, произвольно расположенных в пространстве. Плоскости поворота у разных сил будут различными и должны задаваться дополнительно. Удобно ввести понятие "момент силы относительно центра как в е к т о р", модуль которого равен произведению модуля силы на ее плечо, а направление перпендикулярно плоскости, проходящей через линию действия силы и центр момента.

Вектор момента силы прикладывают в центре момента и направляют в сторону, откуда сила видна вращающей тело в направлении, противоположном ходу часовой стрелки (рис. 1.26). Соединим центр момента О с точкой приложения силы радиусом-вектором и найдем векторное произведение .

По определению векторного произведения его модуль

| |= 2S ∆ ОАВ.

Модуль вектора момента силы также равен удвоенной площади ∆ОАВ. Тогда

‌ ‌ =‌ ‌ .

Направление векторного произведения также совпадает с направлением вектора момента. Следовательно, вектор-момент силы относительно центра О можно рассматривать как векторное произведение радиус-вектора , проведенного из этой точки в точку приложения силы, на вектор силы .

(1.8)

Рис. 1.26 Рис. 1.27

Момент силы относительно оси. Чтобы охарактеризовать вращательный эффект, создаваемый силой, стремящейся повернуть тело вокруг некоторой оси, вводится понятие «момента силы относительно оси».

Рассмотрим твердое тело, которое может вращаться вокруг оси OZ (рис.1.27). Пусть на тело действует сила , приложенная в точке А. Проведем через точку А плоскость OXY, перпендикулярную оси OZ, и разложим силу на две составляющие:, параллельную оси OZ, и , лежащую в плоскости XY. Составляющая, параллельная оси OZ, крутящего момента не создает, а, следовательно, весь вращательный эффект, создаваемый силой ,будет вызван ее составляющей _.

M_z () = M_o () = ± F_xy h = ± 2S ∆OAB₁ (1.9)

Моментом силы относительно оси называют момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.

Момент силы относительно оси считается положительным, если смотря навстречу оси Z, можно видеть проекцию F_xy стремящейся вращать плоскость XY вокруг оси Z в сторону, противоположную вращению часовой стрелки.

Момент силы относительно оси равен нулю:

1) если F_xy = 0, т.е. линия действия силы параллельна оси OZ;

2) если h = 0, т.е. линия действия силы пересекает ось OZ.

Следовательно, если сила и ось лежат в одной плоскости, то момент силы относительно этой оси равен нулю.

Пара сил. Момент пары. Система двух равных по модулю, параллельных и противоположно направленных сил называется п а р о й с и л (рис. 1.28).

Пара сил не имеет равнодействующей и силы пары не уравновешиваются.

Действие пары на тело характеризуется ее моментом.

1. Вектор-момент перпендикулярен плоскости действия пары.

2. Направлен в ту сторону, чтобы, смотря с его конца, вращение было происходящим против хода часовой стрелки.

3. Величина вектора равна в выбранном масштабе численному значению момента пары.

Вектор-момент пары равен векторному произведению радиуса-вектора на ту из сил пары, к началу которой направлен вектор

, (1.10)

или ; (1.11)

по модулю M = r Fsin α = Fh; M =  Fh (1.12)

Пары сил в пространстве эквивалентны, если их моменты геометрически равны. Геометрическая сумма моментов составляющих пар сил равна моменту эквивалентной им пары

(1.13)

Пары сил, произвольно расположенные в пространстве, взаимно уравновешиваются в том случае, если геометрическая сумма их моментов равна нулю. Если пары сил расположены в одной плоскости, то моменты этих пар сил, направленные по одной прямой, складываются а л г е б р а и ч е с к и.

Момент пары сил, эквивалентный системе пар сил на плоскости, равен алгебраической сумме моментов составляющих пар (рис. 1.29).

M =Σ M_i , (1.14)

где M_i = ± F_i d_i . Пары сил, расположенные в одной плоскости, взаимно уравновешиваются, если алгебраическая сумма их моментов равна нулю Σ M_i = 0.

Рис. 1.28 Рис. 1.29

Силовое воздействие на самолет часто приводится к паре сил. Например, аэродинамические силы (силы сопротивления воздуха вращению) воздушного винта складываются в пару, называемую аэродинамическим (реактивным) моментом винта М_в (рис. 1.30). Чем большую мощность развивает двигатель, тем больше реактивный момент, вызывающий крен самолета. Этот момент уравновешивают некоторым отклонением элеронов; аэродинамические силы ._пр и ._лев составляют пару с моментом, равным значению реактивного момента воздушного винта и обратным его направлению.

Рис. 1.30 Рис. 1.31 Рис. 1.32