Классификация кинематических пар

Кинематическая пара и её условное обозначение	Шар-плоскость	Цилиндр-плоскость	Сферическая	Цилиндрическая	Поступательная
			Плоскостная	Сферическая	Вращательная
					Винтовая
	5/1	4/2	3/3	2/4	1/5
	Число степеней свободы / класс пары

Кинематические цепи. Систему звеньев, связанных между собой кинематическими парами, называют кинематической цепью. Если звенья совершают движение в одной плоскости, кинематическая цепь будет плоской, в противном случае – пространственной.

В зависимости от строения кинематическая цепь может быть замкнутой и разомкнутой, простой и сложной. В замкнутой кинематической цепи (рис.3.1а, в) каждое звено входит не менее чем в две кинематические пары, в разомкнутой цепи (рис. 3.1б, г) имеются звенья, входящие лишь в одну кинематическую пару.

Простой (рис. 3.1а, б) называют кинематическую цепь, у которой каждое звено входит в соединение с другим звеном с помощью одной или двух кинематических пар. В противном случае цепь называют сложной (рис.3.1 в, г).

Рис. 3.1

3.2. Основные виды механизмов

Исходя из кинематических, конструктивных и функциональных свойств, механизмы подразделяют на:

1. Рычажные (рис. 3.2а, б)– предназначенные для преобразования вращательного движения входного звена в возвратно-поступательное движение выходного звена. Могут передавать большие усилия и мощности.

2. Кулачковые (рис. 3.2в, г) – предназначенные для преобразования вращательного или возвратно-поступательного движения входного звена в возвратно-поступательное или возвратно-вращательное движение выходного звена. Придавая профилям кулачка и толкателя соответствующие очертания всегда можно осуществить любой желательный закон движения толкателя.

3. Зубчатые (рис. 3.2е) – образованные с помощью зубчатых колес. Служат для передачи вращения между неподвижными и подвижными осями. Зубчатые передачи с параллельными осями осуществляются при помощи цилиндрических зубчатых колес, с пересекающимися осями – при помощи конических зубчатых колес, а со скрещивающимися осями – при помощи червяка и червячного колеса.

4. Фрикционные (рис. 3.2д) – движение от ведущего звена к ведомому передается за счет сил трения, возникающих в результате контакта этих звеньев.

3.3. Структурный синтез и анализ механизмов

Структурным синтезом механизма называется проектирование структурной схемы механизма, которая состоит из неподвижного и подвижных звеньев и кинематических пар. Он является начальной стадией составления схемы механизма, удовлетворяющего заданным условиям. Исходными данными обычно являются виды движения ведущего и рабочего звеньев механизма, взаимное расположение осей вращения и направления поступательного движения звеньев, их угловые и линейные перемещения, скорости и ускорения.Наиболее удобным методом нахождения структурной схемы является метод присоединения структурных групп Ассура к ведущему звену или основному механизму.

Рис. 3.2

Под структурным анализом механизма понимается определение количества звеньев и кинематических пар, определение степени подвижности механизма, а также установление класса и порядка механизма.

Степень подвижности пространственного механизма определяется по формуле Сомова - Малышева:

W = 6n – (5P₁ +4P₂ + 3P₃ + 2P₄ + P₅), (3.1)

где Р_1, Р_2, Р_3, Р_4, Р₅ - число одно-, двух-,трех-, четырех- и пятиподвижных кинематических пар; n – число подвижных звеньев.

Степень подвижности плоского механизма определяется по формуле Чебышева:

W = 3n – 2P_H – P_B, (3.2)

где Р_Н – число низших, а Р_В – число высших кинематических пар.

В качестве примера рассмотрим четырехзвенный механизм рулевого управления автопилота (рис. 3.3): звенья 1 и 2 образуют цилиндрическую пару четвертого класса, имеющую две степени свободы; звенья 2-3 и 4-1 образуют вращательные пары пятого класса, имеющие одну степень свободы;

звенья 3-4 образуют шаровую пару третьего класса, имеющую три степени свободы; число подвижных звеньев равно трем, тогда

W = 6·3 - 2·5 - 1·4 - 1·3 = 1

С

тепень подвижности данного механизма равна 1.

Рис. 3.3

Кинематическая цепь, число степеней свободы которой относительно элементов ее внешних кинематических пар равно нулю, называют структурной группой Ассура, по имени Л.В. Ассура, который впервые фундаментально исследовал и предложил структурную классификацию плоских стержневых механизмов. Пример образования плоского шестизвенного механизма дан на рис.3.4.

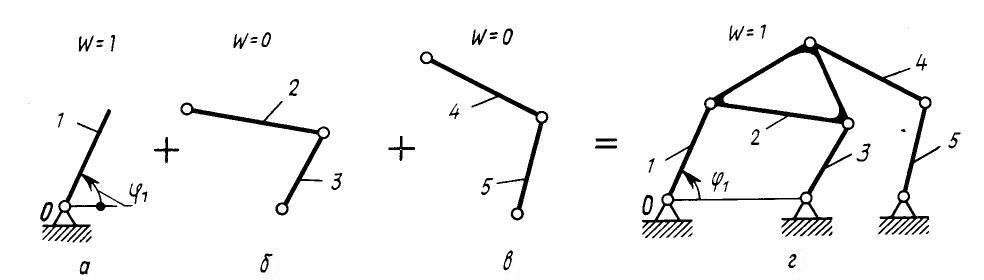
Рис. 3.4

Структурные группы подразделяют по классу и порядку. Класс группы определяется максимальным числом кинематических пар входящих в одно звено (рис. 3.5).

Рис. 3.5

Порядок группы определяется числом элементов, которыми группа присоединяется к основному механизму (рис. 3.6).

Рис. 3.6

Класс и порядок механизма зависят от того, какое звено является ведущим.