
- •Індивідуальне завдання з розділу
- •6.1. Скласти канонічне, загальне та параметричні рівняння прямої, яка проходить через точку м0(х0, у0) та задовольняє умові:
- •6.2. Знайти:
- •6.4. Розв’язати задачу:
- •7.1. Побудувати у полярній системі координат по точках лінію, яка задана своїм рівнянням, змінюючи кут з кроком 15°.
- •7.2. Виконати наступні завдання.
- •7.3. Розв’язати задачу:
7.3. Розв’язати задачу:
Записати рівняння кола, якщо кінці одного з його діаметрів знаходяться у точках А та В.
|
1. A
|
2. A
|
3. A
|
Записати рівняння кола, центр якого знаходиться на вісі абсцис, якщо відомо, що точки А та В належать йому.
|
4. |
5. |
6. |
Дано еліпс Г та точку М, що лежить на ньому. Скласти рівняння прямих, які проходять через точку М та фокуси еліпсу.
|
7.
|
8.
|
9. |
Скласти рівняння гіперболи, яка має спільні фокуси з еліпсом Г та проходить через точку М0.
|
10.
0 |
11.
0 |
12.
0 |
Написати рівняння кола радіусу R, якщо пряма L є дотичною до нього в точці М.
|
13.
L
|
14.
L
|
15.
L
|
Арка мосту має форму параболи. Визначити параметр цієї параболи та записати її рівняння, якщо відомо, що проліт арки дорівнює d м, а висота h м.
|
16.
|
17.
|
18.
|
Крізь лівий фокус еліпсу Г проведено перпендикуляр до його великої вісі. Визначити відстань від точок перетину цього перпендикуляру з еліпсом до фокусів.
|
19.
|
20.
|
21.
|
Сталевий
трос підвішений за два кінці; точки
кріплення розташовані на однаковій
висоті, відстань між ними d м. Величина
його прогину на відстані
![]() м
від точки кріплення (по горизонталі)
дорівнює h см. Визначити величину h0
прогину цього тросу в середині між
точками кріплення, якщо вважати що трос
має форму дуги параболи.
м
від точки кріплення (по горизонталі)
дорівнює h см. Визначити величину h0
прогину цього тросу в середині між
точками кріплення, якщо вважати що трос
має форму дуги параболи.
|
22.
|
23.
|
24.
|
Визначити,
при яких значеннях параметру m
пряма
![]() 1) перетинає еліпс Г; 2) торкається еліпса
Г; 3) проходить поза еліпсу Г.
1) перетинає еліпс Г; 2) торкається еліпса
Г; 3) проходить поза еліпсу Г.
|
25.
|
26.
|
27.
|
Під гострим кутом до горизонту кинуто камінь, який рухаючись по параболі, впав на відстані S м від початкового положення. Знайти рівняння траєкторії , якщо відомо, що найбільша висота, яку досягнув камінь, дорівнює h м.
|
28.
S |
29.
S |
30.
S |
7.4. Дано параметричні рівняння кривої. Виключенням параметру t знайти рівняння даної кривої у вигляді F(х,у) = 0 та побудувати її.
1.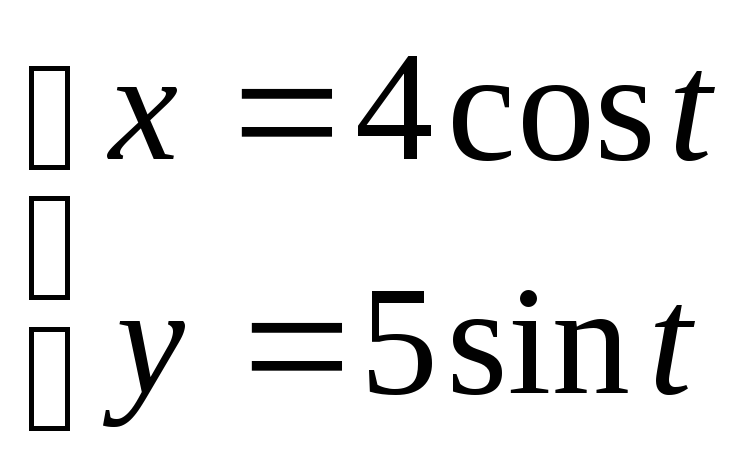 ; 2.
; 2.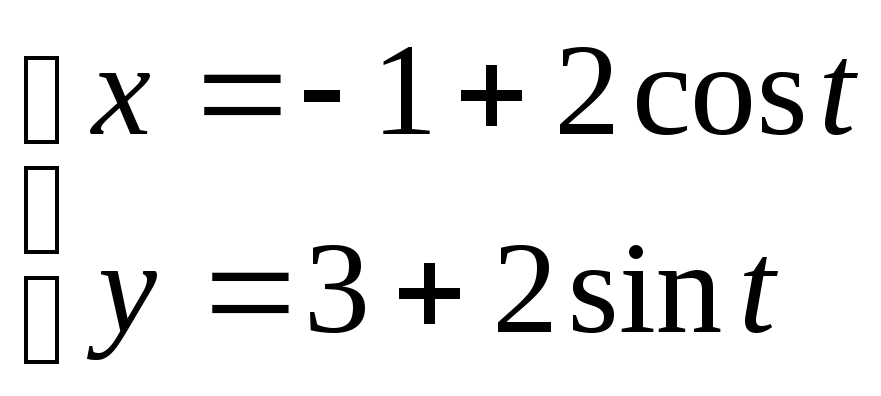 ;
3.
;
3.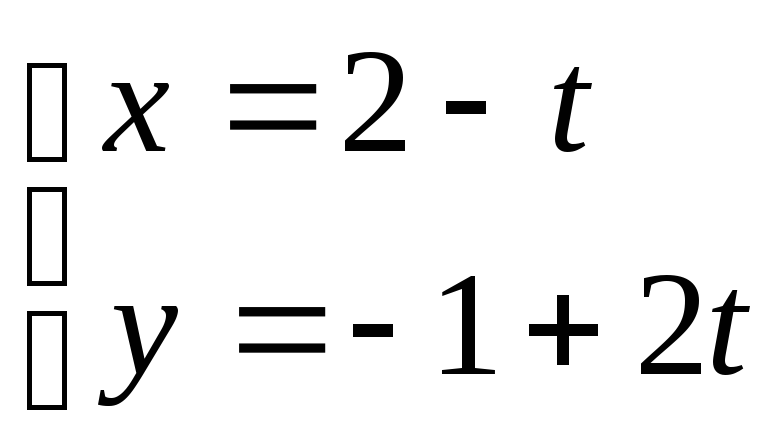 ;
;
4.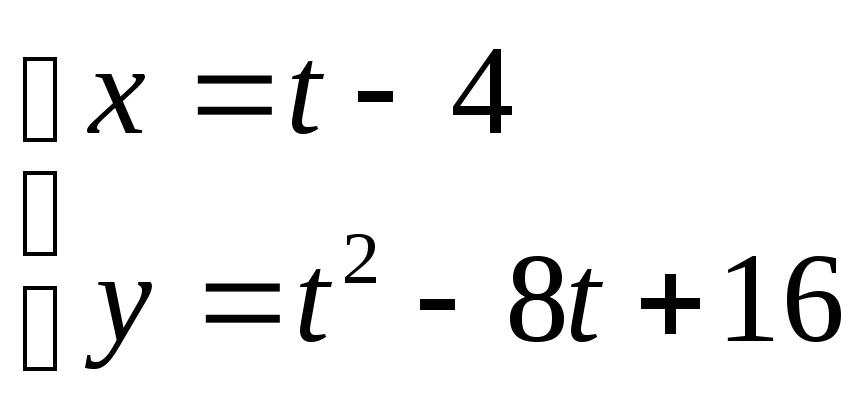 ; 5.
; 5.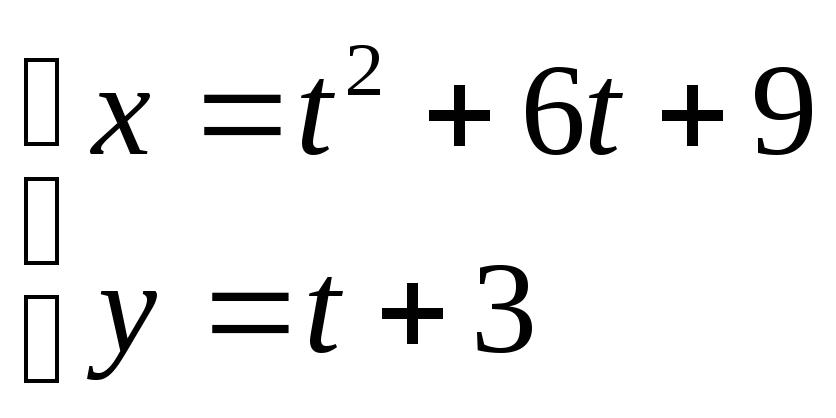 ;
6.
;
6.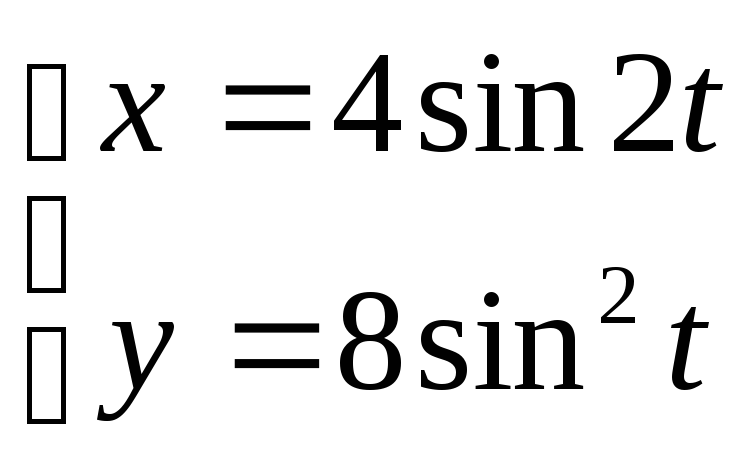 ;
;
7.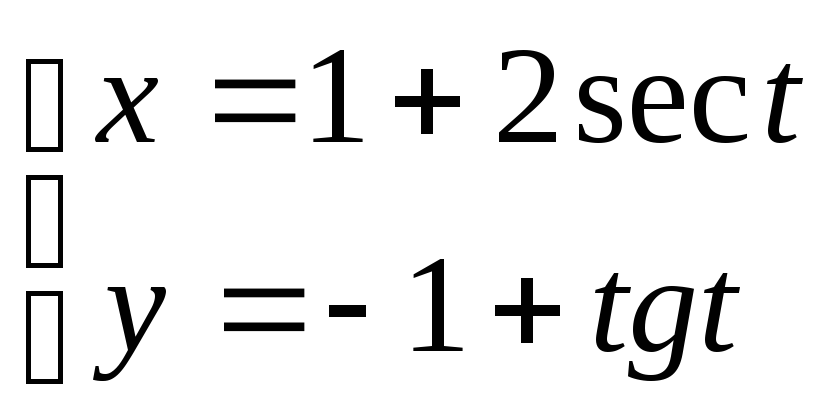 ;
8.
;
8.
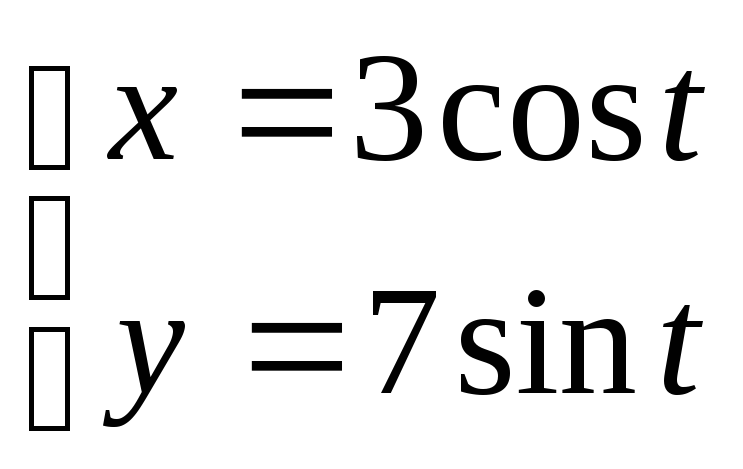 ; 9.
; 9.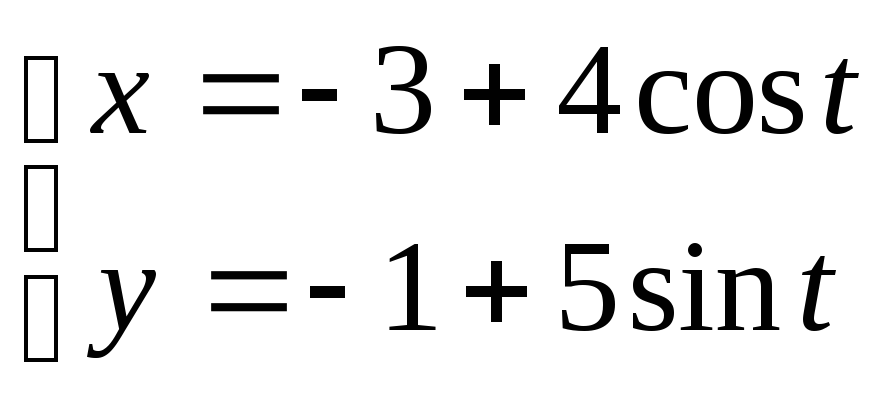 ;
;
10.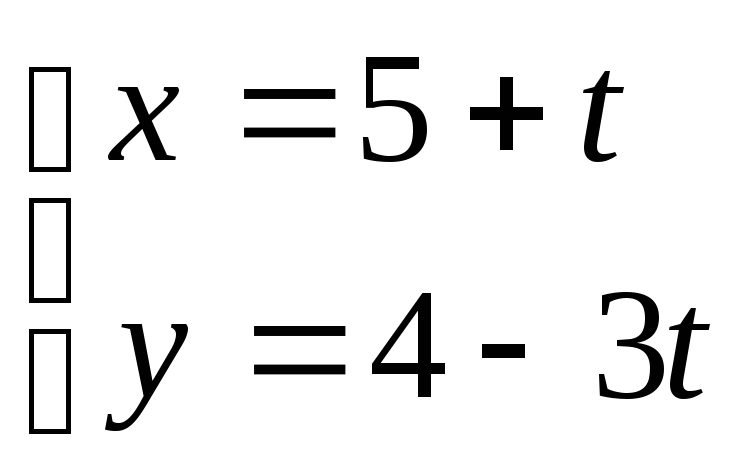 ; 11.
; 11.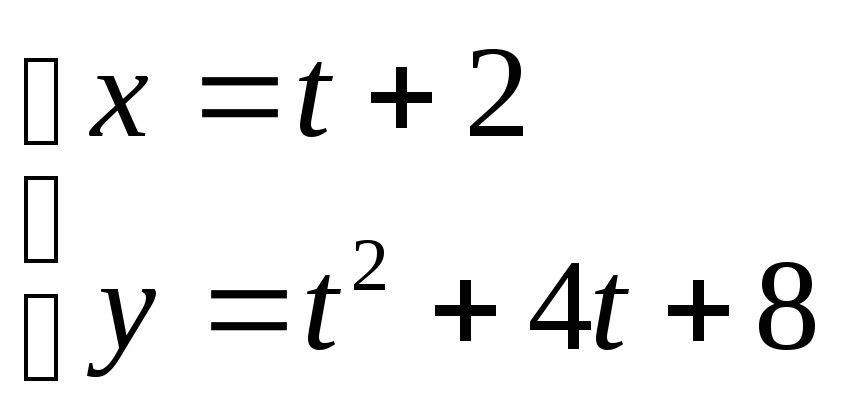 ;
12.
;
12.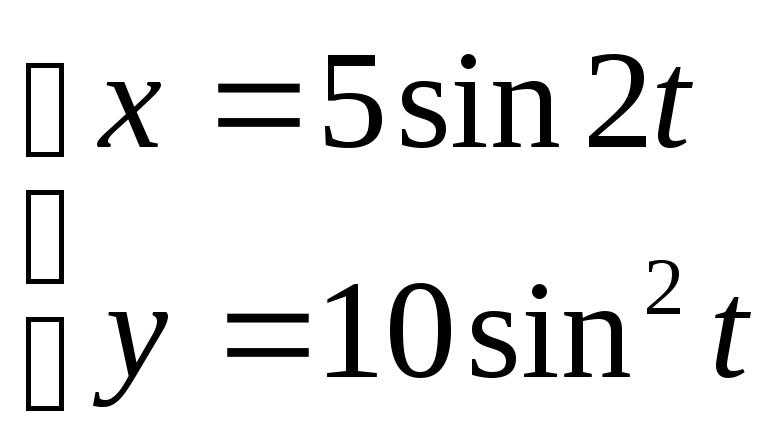 ;
;
13.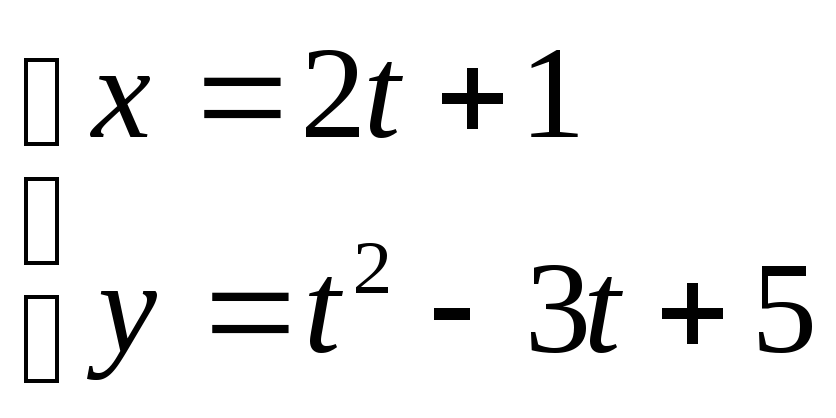 ;
14.
;
14.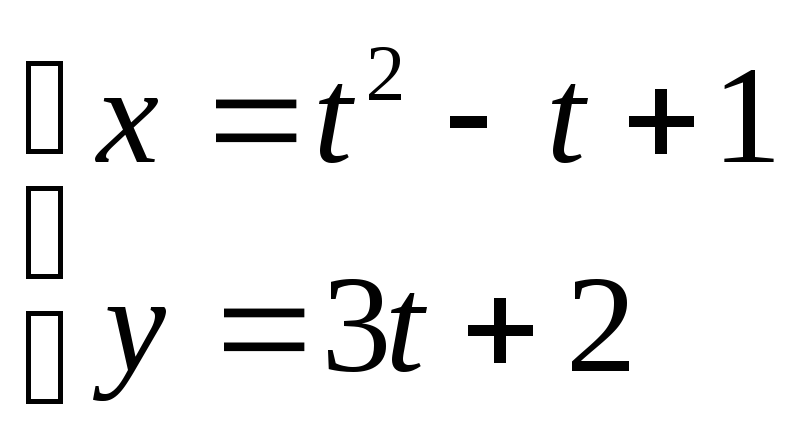 ;
15.
;
15.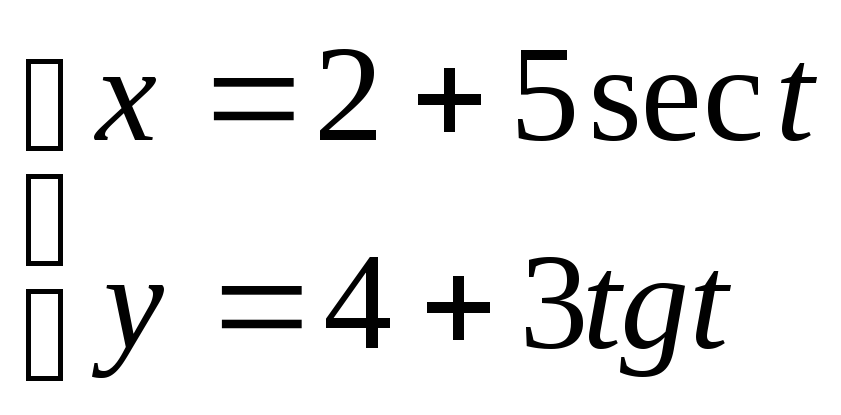 ;
;
16.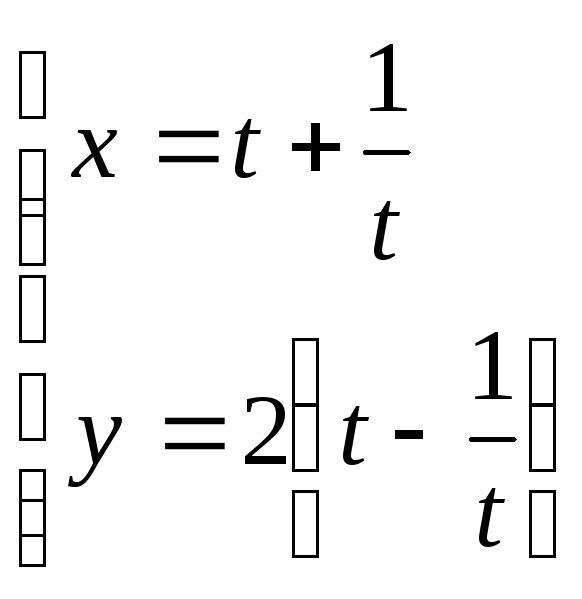 ;
17.
;
17.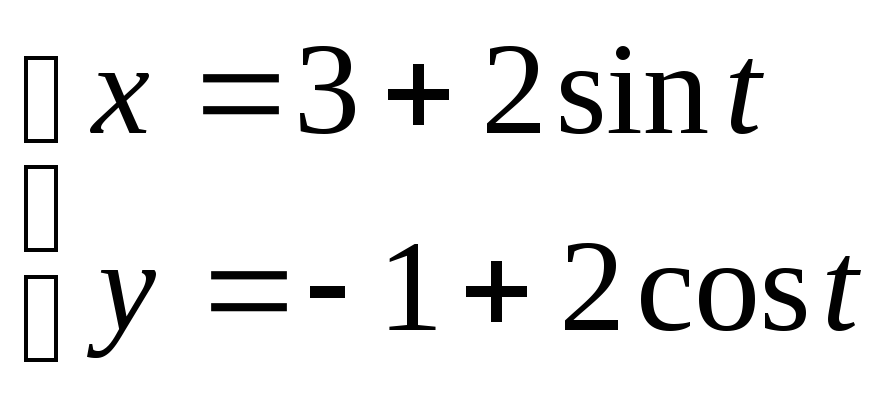 ;
18.
;
18.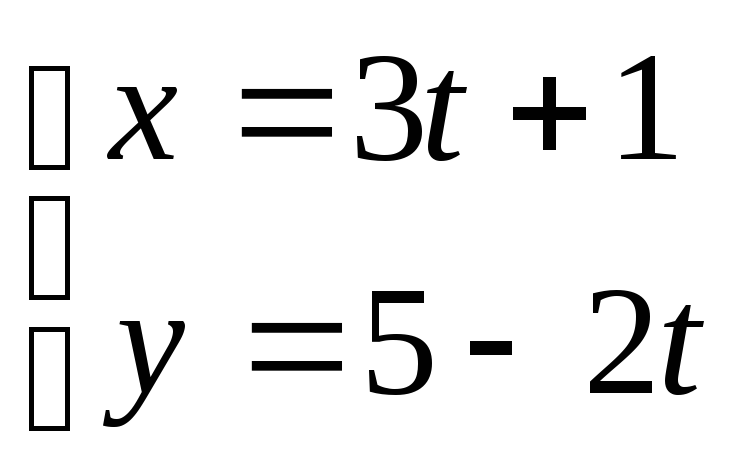 ;
;
19.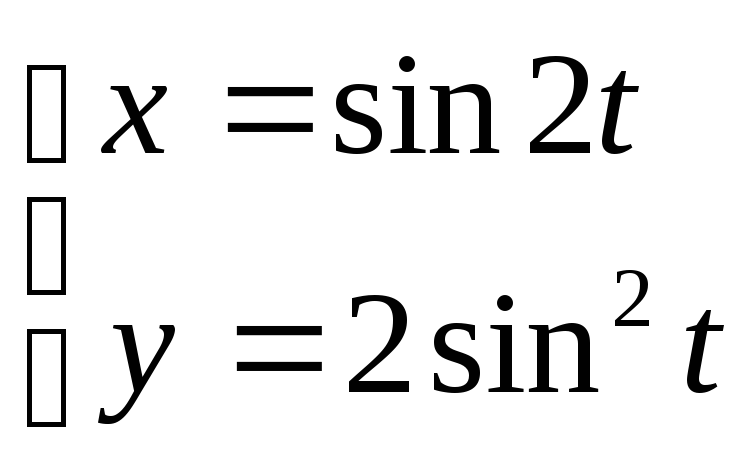 ;
20.
;
20.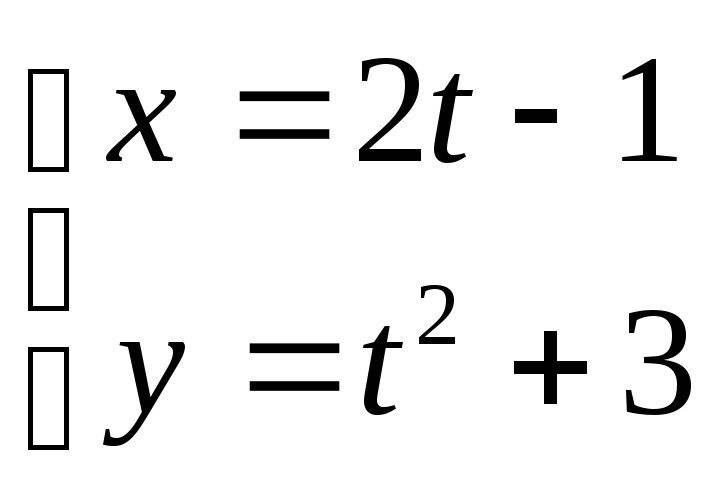 ;
21.
;
21.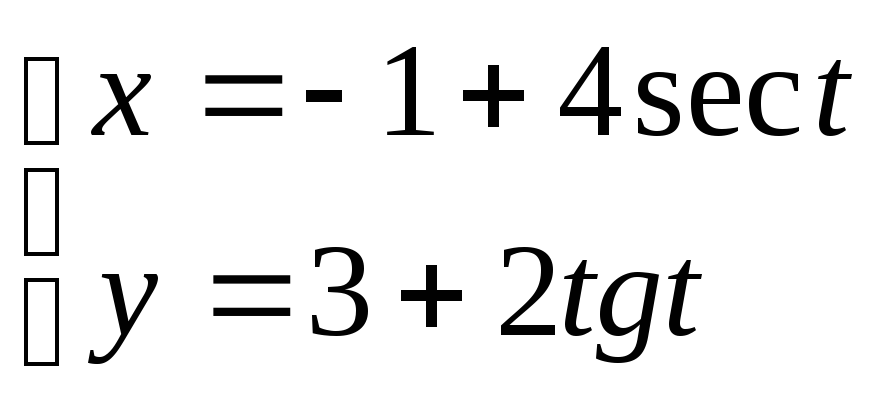 ;
;
22.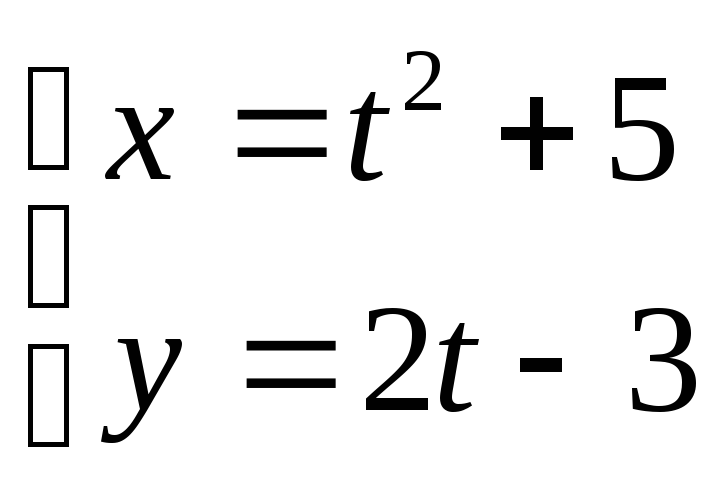 ; 23.
; 23.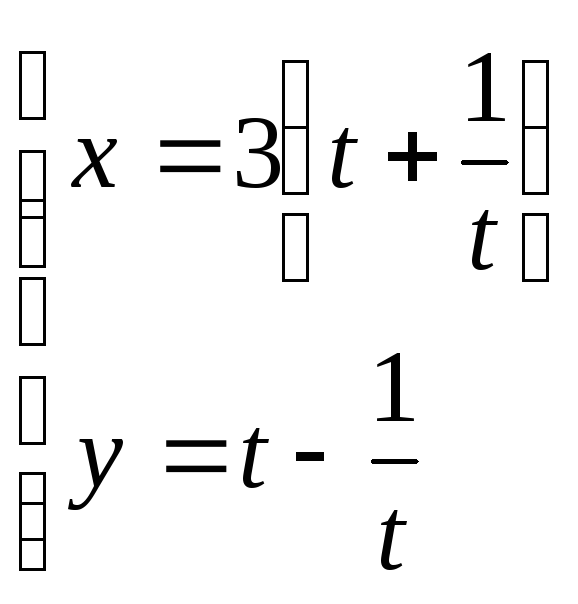 ;
24.
;
24.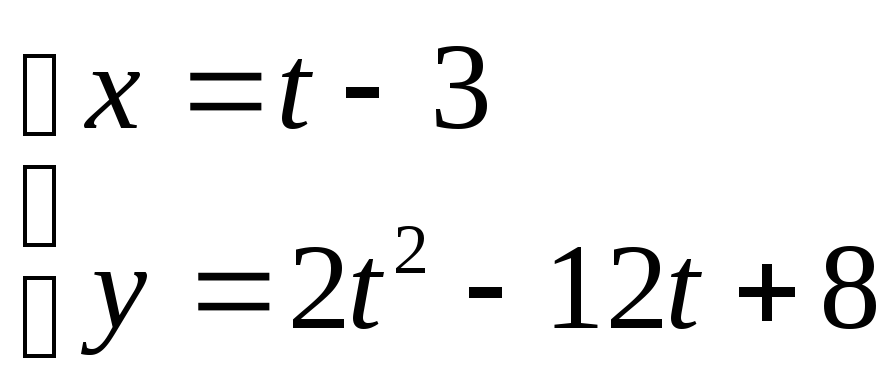 ;
;
25.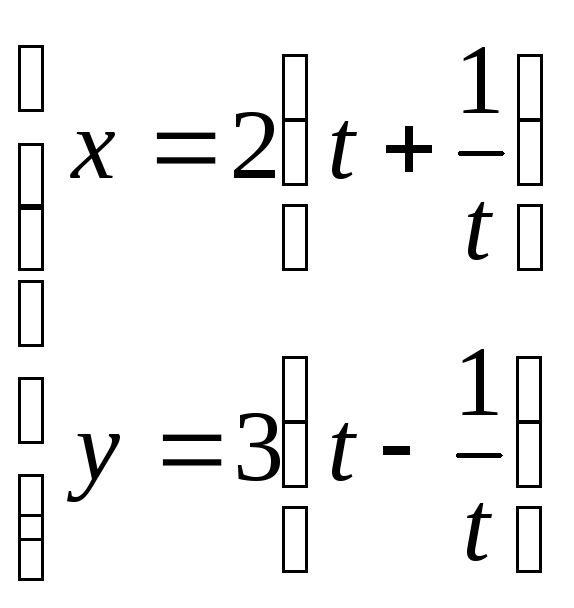 ; 26.
; 26.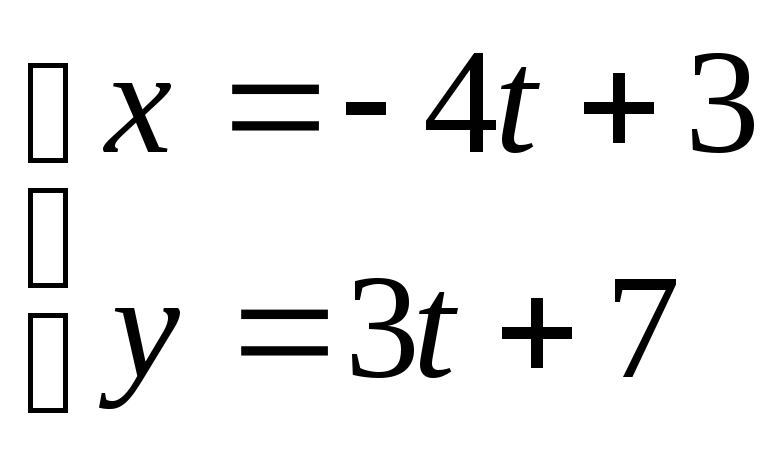 ; 27.
; 27.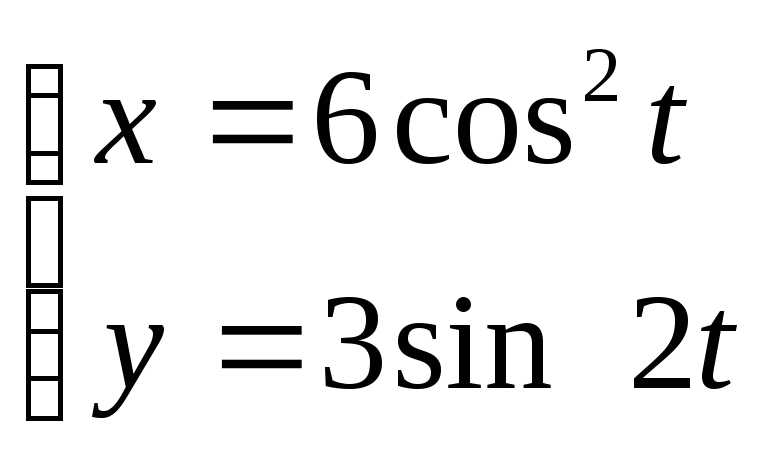 ;
;
28.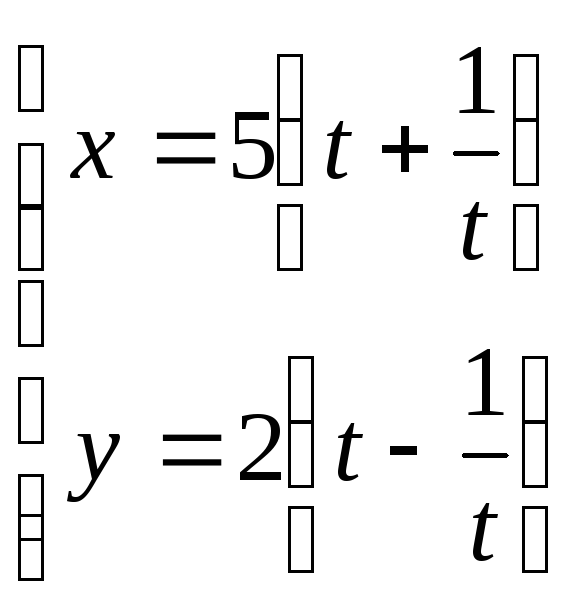 ;
29.
;
29.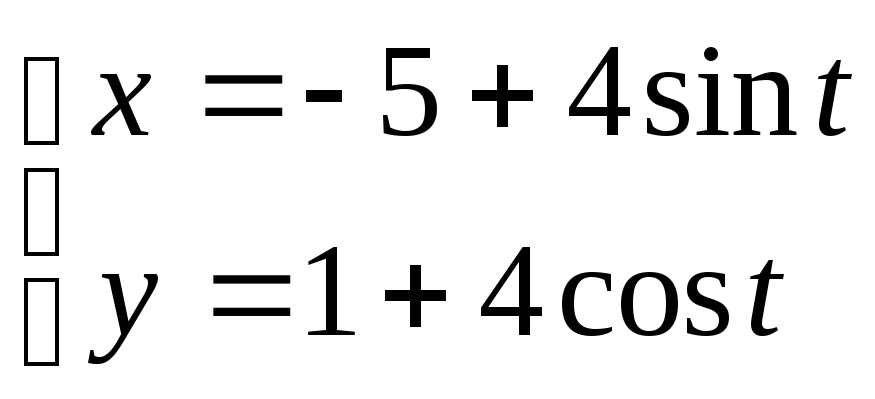 ;
30.
;
30.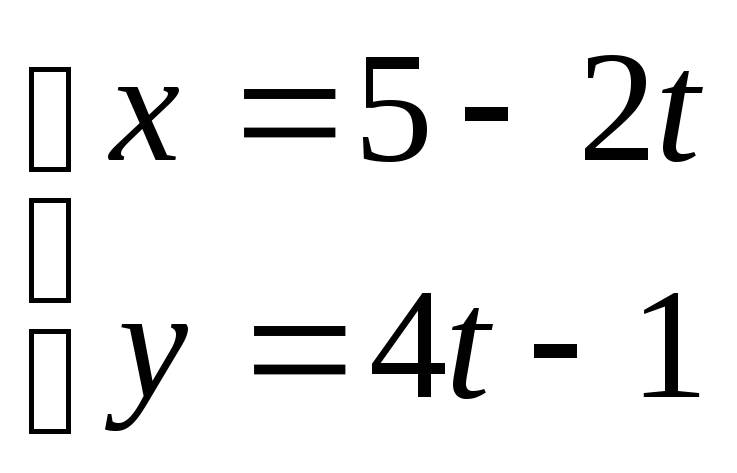 .
.
8.4. Дано вершини трикутника А(х1;у1), В(х2;у2), С(х3;у3). Знайти:
-
рівняння всіх його сторін;
-
рівняння медіани та висоти, які проведені з вершини В, та кут між ними;
-
рівняння перпендикуляру, який проведено з вершини А на медіану, що виходить з вершини В, та точку їх перетину;
-
довжину висоти, проведеної з вершини В;
-
рівняння прямої, яка проходить через вершину С паралельно протилежній стороні;
-
рівняння бісектрис внутрішнього то зовнішнього кутів при вершині С.
|
варіант |
|
|
|
|
|
|
варіант |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
17 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
19 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
22 |
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
23 |
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
26 |
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
27 |
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
28 |
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
29 |
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
30 |
|
|
|
|
|
|
8.5. Скласти рівняння траєкторії руху точки М(х;у), котра у будь-який момент часу задовольняє умови:
1. Точка М рівновіддалена від точки А(-3;2) та вісі ординат.
2. Сума квадратів відстаней від точки М до точок А(4;0) та В (-2;2) дорівнює 28.
3. Точка М рівновіддалена від точок А(5;-2) та В(-3;-2).
4. Різниця квадратів відстаней від точки М до точок А(3;-1) та В(1;2) дорівнює 17.
5. Відношення відстаней від точки М до точок А(2;3) та В(-1;2) дорівнює 0,75.
6. Точка М віддалена від прямої х = -3 на відстань у два рази більшу, ніж від точки А(3;2).
7. Точка М удвічі ближча до точки А(1;0), ніж до точки В(4;0).
8. Відношення відстаней від точки М до початку координат та до точки А(5;0) дорівнює 2.
9. Точка М рівновіддалена від точки А(0;4) та від прямої у = 8.
10. Сума відстаней від точки М до точок А(-3;0) та В(3;0) дорівнює 10.
11. Різниця відстаней від точки М до точок А(-4;0) та В(4;0) дорівнює 6.
12. Точка М рівновіддалена від точки А(5;5) та від вісі абсцис.
13. Сума квадратів відстаней від точки М до точок А(3;0) та В(-3;0) дорівнює 50.
14. Точка М рівновіддалена від точок А(-3;5) та В(2;7).
15. Точка М рівновіддалена від вісі ординат та від точки А(4;-2).
16. Відношення відстаней від точки М до точки А(-4;0) та до початку координат дорівнює трьом.
17. Різниця квадратів відстаней від точки М до точок А(-2;3) та В(1;2) дорівнює 13.
18. Відношення відстаней від точки М до точок А(-1;1) та В(1;0) дорівнює 0,5.
19. Сума відстаней від точки М до точок А(-1;0) та В(1;0) дорівнює 6.
20. Різниця відстаней від точки М до точок А(-6;0) та В(6;0) дорівнює 8.
21. Точка М рівновіддалена від точки А(-4;6) та від прямої х = 4.
22. Точка М рівновіддалена від точок А(-1;-1) та В(0;2).
23. Відношення відстаней від точки М до точок А(1;0) та В(0;2) дорівнює 2.
24. Відношення відстаней від точки М до точки А(2;3) та до прямої у = -3 дорівнює 0,5.
25. Точка М рівновіддалена від точки А(4;6) та від прямої у = 2.
26. Точка М рівновіддалена від точок А(-3;5) та В(1;2).
27. Різниця квадратів відстаней від точки М до точок А(-1;0) та В(0;2) дорівнює 3.
28. Сума відстаней від точки М до точок А(-5;0) та В(5;0) дорівнює 14.
29. Різниця відстаней від точки М до точок А(-7;0) та В(7;0) дорівнює 10.
30. Різниця квадратів відстаней від точки М до точок А(1;2) та В(4;6) дорівнює 3.
