
- •Практические занятия
- •2). (Задание для самостоятельного решения).
- •2). (Задание для самостоятельного решения).
- •2). (Задание для самостоятельного решения).
- •2). (Задание для самостоятельного решения).
- •4). (Задание для самостоятельного решения).
- •3). (Задание для самостоятельного решения).
- •2). (Задание для самостоятельного решения).
- •Исполнительский блок
- •Контролирующий блок
Практические занятия
Семинар № 5.1 (14). Основные элементарные функции, их графики преобразования.
-
Определить и построить на числовой оси области изменения переменных х, t, α, заданные следующими неравенствами
 ;
;
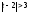 ;
;
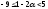 .
.
Решение.
1).
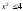 ═>
═> ═> -2≤х≤2.
Ответ.
═> -2≤х≤2.
Ответ.
![]() .
.
2).
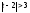 ═>
═>
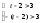 ═>
═>
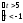 ═>
═>
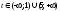 .
Ответ.
.
Ответ.
![]() .
.
3). (Задание для самостоятельного решения).
-
Вычислить частное значение функции:
1).
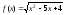 при х=0, х=а+1; 2).
при х=0, х=а+1; 2).
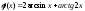 при х=-1/2.
при х=-1/2.
Решение.
1).
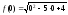 =2.
=2.
2). (Задание для самостоятельного решения).
Ответ.
1). 2; 2).
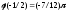 .
.
-
Определить четность функций:
1).
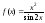 ;
2).
;
2).
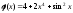 ;
3).
;
3).
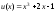 ;
4).
;
4).
 .
.
Решение.
1). Вычислим
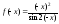 =
=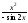 =
= .
Значит, функция нечетная.
.
Значит, функция нечетная.
Задания 2), 3), 4) для самостоятельного решения.
Ответ. 1). Нечетная. 2). Четная. 3). Не является ни четной, ни нечетной. 4). Нечетная при х≠0. При х=0 функция у(х) не существует.
-
Найти область определения функций: 1).
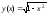 ;
2).
;
2).
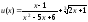 ;
;
3).
 ;
4).
;
4).
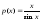 ;
5).
;
5).
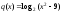 .
.
Решение.1).
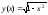 ═> 1-х2≥0
═>
═> 1-х2≥0
═>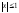 ═>-1≤х≤1.
═>-1≤х≤1.
Задания 2), 3), 4), 5) для самостоятельного решения.
Ответ.
1). -1≤х≤1.
2). х≠2
и х≠3.
3).
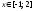 ;
4). х≠kπ,
k
;
4). х≠kπ,
k Z,
5).
Z,
5).
 .
.
-
Найти область изменения функций: 1).
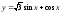 ;
2).
;
2).
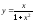 .
.
Решение.
1).
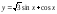 =>
=> =>
=>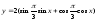 =>
=>
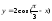 .
.
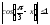 ,
значит,
,
значит,
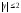 ,
или
,
или
 .
.
Ответ.
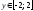 .
.
2).
Из функции
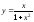 выразим х
через у,
получим
выразим х
через у,
получим
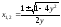 .
Это выражение имеет смысл, если
.
Это выражение имеет смысл, если
1-4у2≥0
или
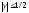 .
.
Ответ.
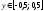 .
.
-
Найти наименьший период функций: 1).
 ;
2).
;
2).
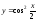 .
.
Решение.
1).
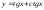 =>
=>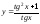 =>
=>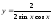 =>
=>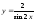 =>
=>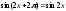 => x=x+π
=>T=π.
=> x=x+π
=>T=π.
2). (Задание для самостоятельного решения).
Ответ. 1). T=π. 2). Т=2π.
Семинар № 5.2 (15). Основные элементарные функции, их графики преобразования.
-
Построить график функций:
1).
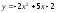 ;
2).
;
2).
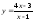 ;
3).
;
3).
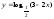 ;
4).
;
4).
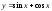 .
.
-
Построить график функции, заданной параметричеки:
1).
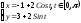
 ;
2).
;
2).
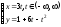 .
.
Решение. 1). Составим таблицу значений переменных х и у в зависимости от параметра t и построим график в декартовой прямоугольной системе координат
|
t |
0 |
π/4 |
π/2 |
3π/4 |
π |
|
|
x |
1 |
-1+ |
-1 |
-1- |
-3 |
|
|
y |
3 |
3+ |
5 |
3- |
3 |
Это
построение можно выполнить другим
способом. Из задания функции исключим
параметр t,
получим
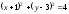 .
Это уравнение окружности с центром в
точке (-1; 3) и радиусом r=2.
Так как t
.
Это уравнение окружности с центром в
точке (-1; 3) и радиусом r=2.
Так как t [0;π),
то sint≥0,
значит у≥3,
то есть имеем часть окружности, лежащую
выше прямой у=3.
[0;π),
то sint≥0,
значит у≥3,
то есть имеем часть окружности, лежащую
выше прямой у=3.
2). (Задание для самостоятельного решения).
-
В полярной системе координат построить кривую, давая значения
 через
через
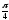 от 0 до
от 0 до
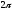 .
Найти уравнение кривой в декартовой
прямоугольной системе координат. Найти
полярное уравнение кривой и построить
ее:
.
Найти уравнение кривой в декартовой
прямоугольной системе координат. Найти
полярное уравнение кривой и построить
ее:
1).
а).
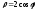 ;
б).
;
б).
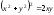 . 2).
а).
. 2).
а).
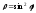 ;
б).
;
б).
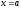 .
.
Решение.
1). а).
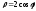 .
Составим таблицу значений ρ
(ρ
≥0) в зависимости от угла φ.
.
Составим таблицу значений ρ
(ρ
≥0) в зависимости от угла φ.
|
φ |
0 |
π/4 |
π/2 |
3π/4 |
π |
5π/4 |
3π/2 |
7π/4 |
2π |
|
ρ |
2 |
|
0 |
- |
- |
- |
0 |
|
2 |
Построим график в полярной системе координат, совместив ее с декартовой прямоугольной системой координат
|
|
Чтобы
найти уравнение линии
Получим
|
б).
Для нахождения полярного уравнения
линии
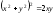 воспользуемся уже известными формулами
из предыдущего примера. Получим
воспользуемся уже известными формулами
из предыдущего примера. Получим
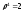
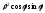 или
или
 .
Составим следующую таблицу значений:
.
Составим следующую таблицу значений:
|
φ |
0 |
π/4 |
π/2 |
3π/4 |
π |
5π/4 |
3π/2 |
7π/4 |
2π |
|
ρ |
0 |
1 |
0 |
- |
0 |
1 |
0 |
- |
0 |
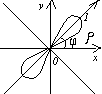
Построим
график в полярной системе координат.
 .
.

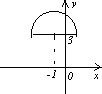

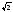
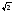
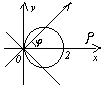
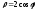 в декартовой системе координат, надо
применить формулы, связывающие
декартовые и полярные координаты
точки, то есть
в декартовой системе координат, надо
применить формулы, связывающие
декартовые и полярные координаты
точки, то есть
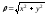 ;
;
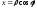 ;
;
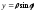 ;
;
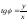 ,
,
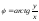 .
.
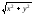 =2
=2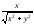 ,
или
,
или
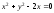 .
Это уравнение окружности с центром в
точке (1; 0) и радиусом r
=1.
.
Это уравнение окружности с центром в
точке (1; 0) и радиусом r
=1.