
- •1. Множества и операции над ними
- •1.1. Множества. Определения, примеры. Способы задания множеств
- •Способы задания множеств
- •I. Задание множества списком
- •II. Порождающая процедура
- •III. Задание множества описанием его элементов (разрешающая процедура)
- •1.2.Операции над множествами
- •2.Векторы и прямые произведения
- •2.1. Векторы
- •2.1.Проекции векторов и векторных множеств на оси
- •3. Элементы комбинаторики
- •3.1. Правило произведения
- •3.2. Размещения без повторений
- •3.3. Размещения с повторениями
- •3.4. Перестановки без повторений
- •3.5. Перестановки с повторениями
- •3.6. Сочетания без повторений
- •3.6. Правило суммы
- •4. Соответствия
- •4.1 Определения и примеры
- •4.2. Взаимно однозначные соответствия и мощность множеств
- •4.3. Счетные множества
- •О парадоксе Кантора
- •5. Отношения
- •5.1. Определения и примеры
- •5.2. Способы задания бинарных отношений
- •5.3. Свойства отношений
- •5.4. Отношение эквивалентности
- •Классы эквивалентности
- •5.5. Отношение порядка
- •6. Элементы общей алгебры
- •6.1. Алгебры
- •6.2. Свойства бинарных алгебраических операций
- •6.3.Гомоморфизм и изоморфизм алгебр
- •7. Булева алгебра и теория множеств
- •7.1. Основные определения
3.6. Сочетания без повторений
Решим задачу:
сколькими способами из множества
![]() можно составить всевозможные подмножества
по k элементов каждое?
можно составить всевозможные подмножества
по k элементов каждое?
Число таких
подмножеств будем называть числом
сочетаний без повторений из n элементов
по k и обозначать
![]() .
Решить ее проще всего тоже исходя из
понятия вектора. Если бы мы искали число
упорядоченных k - подмножеств без
повторений, составленных из множества
Х в n элементов, то оно было бы равно
.
Решить ее проще всего тоже исходя из
понятия вектора. Если бы мы искали число
упорядоченных k - подмножеств без
повторений, составленных из множества
Х в n элементов, то оно было бы равно
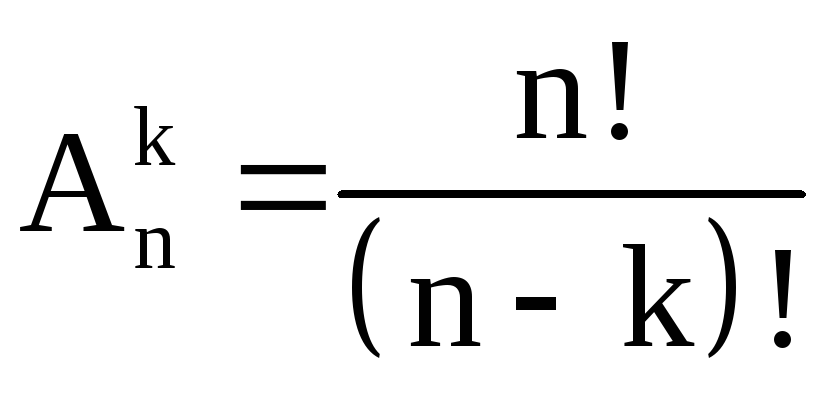 .
.
Но нас не интересует
порядок элементов, выбранный в вектор
длины k, а интересует лишь состав. Тогда
среди
![]() Различных векторов k! штук имеют одинаковые
компоненты и отличаются лишь их порядком.
Таким образом, сочетаний будет в k! раз
меньше, чем размещений
Различных векторов k! штук имеют одинаковые
компоненты и отличаются лишь их порядком.
Таким образом, сочетаний будет в k! раз
меньше, чем размещений
![]() .
.
Пример:
Из 1, 2, 3, 4
упорядоченных пар можно составить
![]() .
.
12 13 14 23 24 34
21 31 41 32 42 43
При таком расположении
заметно, что эти пары можно составить,
выбрав сначала в пару какие-то 2 элемента,
а затем составить все возможные векторы,
переставив данный состав 2! различными
способами. Значит, если считать пары,
отличающиеся только составом, то их
будет в 2! раз меньше, чем
![]() .
.
Пример:
Сколько существует различных способов заполнения карточек “Спортлото” 6 из 49? Нам надо выбрать неупорядоченные подмножества длины k = 6 из множества Х, n = 49.
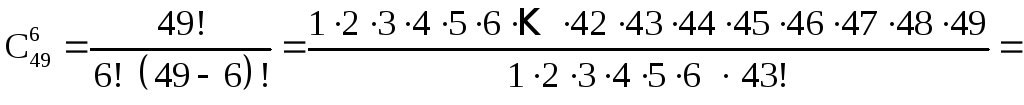
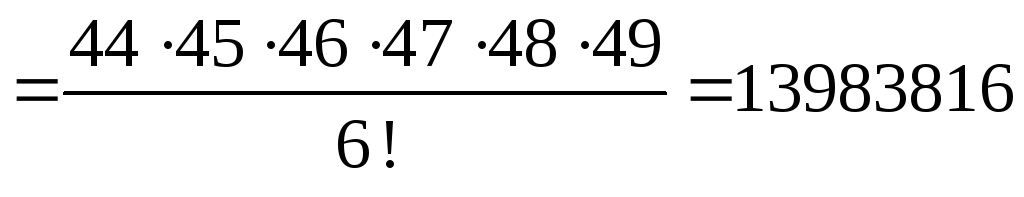 .
.
3.6. Правило суммы
Решим задачу: в вазе лежат 6 яблок и 12 груш. Сколько в ней плодов? Ответ тривиален: 6 + 12 = 18. Если выбрать из вазы один лежащий в ней плод, то это можно сделать 18 способами. Вообще справедлив следующий принцип комбинаторики: если объект а можно выбрать m способами, а объект b выбрать n способами, то выбор “а или b” можно сделать m + n способами.
На языке теории множеств это утверждение означает, если
![]() и
и
![]() ,
то
,
то
![]() .
.
Сложнее получить ответ, когда А и В пересекаются.
Пусть![]() .
Тогда, находя
.
Тогда, находя
![]() ,
мы к мощности (числу элементов) А прибавим
число элементов в В, причем число
элементов
,
мы к мощности (числу элементов) А прибавим
число элементов в В, причем число
элементов
![]() попадет в сумму дважды: один раз - в
слагаемом
попадет в сумму дважды: один раз - в
слагаемом
![]() ,
второй - в слагаемом
,
второй - в слагаемом
![]() .
Поэтому из
.
Поэтому из
![]() нужно один (лишний) раз
нужно один (лишний) раз
![]() - вычесть.
- вычесть.
![]() .
.
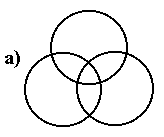
![]() непусто (рис.а), то его элементы в случае
см. выше окажутся совсем неучтенными:
сначала их три раза учитывают, когда
складывают мощности каждого из трех
множеств А, В и С, а потом те же три раза
учитывают, вычитая мощности пересечений
множеств по два. Эти операции гасят друг
друга, и полученный ответ окажется
меньше истинного как раз на число
элементов
непусто (рис.а), то его элементы в случае
см. выше окажутся совсем неучтенными:
сначала их три раза учитывают, когда
складывают мощности каждого из трех
множеств А, В и С, а потом те же три раза
учитывают, вычитая мощности пересечений
множеств по два. Эти операции гасят друг
друга, и полученный ответ окажется
меньше истинного как раз на число
элементов![]() .
Значит, это число и надо добавить.
.
Значит, это число и надо добавить.
![]() .
.
Общее правило для
![]() выглядит так:
выглядит так:
![]()
![]()
![]() .
.
Пример: Во время отпуска 12 дней шел дождь, 8 дней дул сильный ветер, причем 5 дней были дождливы и ветренны. Сколько было дней с плохой погодой?
12 + 8 - 5 = 15.
4. Соответствия
4.1 Определения и примеры
Определение:
Соответствием
множества А и В называется подмножество
G,
![]() .
.
Если
![]() ,
то говорят,
что “b
соответствует a при соответствии G”.
,
то говорят,
что “b
соответствует a при соответствии G”.
Определение: Область определения соответствия G - множество пр1 G.
Определение: Область значений соответствия G - множество пр2G.
Определение: Соответствие G называется всюду (полностью) определенным - если пр1 G = А (в противном случае - частично определенное соответствие).
Определение: Соответствие G называется сюрьективным - если пр2 G = B.
Определение:
Образ элемента
a
в множестве B
при соответствии G - множество всех
элементов![]() ,
которые соответствуют
,
которые соответствуют
![]() .
.
Определение:
Прообраз
элемента b
в множестве А
при соответствии G - множество всех![]() ,
которым соответствует
,
которым соответствует
![]() .
.
Определение:
Образом
множества С![]() пр1 G,
то называется объединение образов всех
элементов С.
пр1 G,
то называется объединение образов всех
элементов С.
Определение:
Прообразом
множества D![]() пр2 G
называется объединение прообразов всех
элементов D.
пр2 G
называется объединение прообразов всех
элементов D.
Определение: G называется функциональным (однозначным) соответствием если образом любого элемента из пр1 G является единственный элемент из пр2 G.
Определение: G называется инъективным соответствием если прообразом любого элемента из пр2 G является единственный элемент из пр1 G.
Определение:
Соответствие
G является функцией
типа![]() ,
если оно функционально.
,
если оно функционально.
Определение: Соответствие G является отображением множества А в множество В, если оно функционально и полностью определено.
Определение: Соответствие G является взаимно однозначным, если оно:
1) всюду определено;
2) сюрьективно;
3) функционально;
4) инъективно.
Пример:
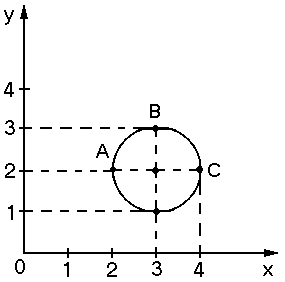
![]() .
.
Круг G задает соответствие между R и R (осью абсцисс и осью ординат). Образом числа 4 оси абсцисс при этом соответствии является единственное число 2 оси ординат. Образом числа 3 оси абсцисс - отрезок [1; 3] оси ординат. Отрезок [1; 3] оси ординат является образом отрезка [2; 4] оси абсцисс. Отрезок [2; 4] оси абсцисс является прообразом числа 2 оси ординат.
Данное соответствие - нефункциональное, так как, например, точке 3 абсцисс соответствует не одна точка, а отрезок.
Примером функционального соответствия является соответствие, заданное дугой АВС. Но оно не является инъективным, так как прообразом, например, точки 2 оси ординат является не одна точка, а отрезок [2, 4].
Напомним, что для задания соответствия надо указать:
а) множество G;
б) множество А и В, то есть указать, подмножеством какого прямого произведения является G.
В данном примере
круг G задает и другое соответствие:
между отрезками [2, 4] и отрезком [1, 3]. При
этом соответствие
![]() и
и
![]() отличаются по некоторым свойствам.
Например, второе соответствие
отличаются по некоторым свойствам.
Например, второе соответствие
![]() в отличие от первого
в отличие от первого
![]() ,
всюду определено и сюрьективно. Поэтому
следовало бы определять соответствие
через тройку множеств (G, A, B), тогда не
пришлось бы оговариваться, что один
круг может задавать два соответствия.
Это и так было бы ясно из различия троек
,
всюду определено и сюрьективно. Поэтому
следовало бы определять соответствие
через тройку множеств (G, A, B), тогда не
пришлось бы оговариваться, что один
круг может задавать два соответствия.
Это и так было бы ясно из различия троек
![]() и
и
![]() .
.
Но такие оговорки приходится делать редко:
- либо множества А и В ясны из контекста;
- либо различия в их выборе не влияют на исследуемые свойства соответствия.
Пример:
Множество векторов
вида
![]() ,
где
,
где
![]() задает взаимно однозначное соответствие
между множествами N - натуральных чисел
и множеством
задает взаимно однозначное соответствие
между множествами N - натуральных чисел
и множеством
![]() степеней двойки.
степеней двойки.
