7. Булева алгебра и теория множеств

7.1. Основные определения

Будем рассматривать двухэлементное множество , элементы которого не являются числами в полном смысле этого слова, а интерпретируются как «ложь» и «истина». Считая их логическими переменными, определим следующие функции алгебры двузначной логики.

Определение:

Отрицанием x назовем функцию , которая значению аргумента x = 0 ставит в соответствие ; а значению аргумента x = 1 ставит в соответствие .

Определение:

Конъюнкцией элементов и назовем функцию , которая имеет значение 1, только если . В остальных случаях конъюнкция равна 0.

Определение:

Дизъюнкцией элементов и назовем функцию , которая принимает значение 1, если хотя бы один из ее аргументов или (то есть только , или только , или и одновременно) равны 1. Дизъюнкция равна нулю тогда и только тогда, когда .

Определенные так логические функции носят название логических связок «не», «и», «или».

Связь между ними описывается с помощью набора эквивалентностей:

1) ; 2) ;

3) ; 4) ;

5); 6);

7) ; 8) ;

9) ; 10) ;

11) ; 12) ;

13) ; 14) ;

.

Любые операции, подчиняющиеся свойствам 1-14, называются булевыми операциями. F алгебры с данным набором операций называются булевыми алгебрами. Так, например, свойства 1-14 будут выполняться и для операций объединения, пересечения и дополнения множеств, если сопоставить

объединение – дизъюнкции;

пересечение – конъюнкции;

дополнение – отрицанию, а вместо и подставить некоторые множества А и В из U (универсального множества).

Заметим важный факт, что если применить данные операции к логическим функциям , где , то результатами тоже будут логические функции. Поэтому связки &, также можно считать и операциями над множеством всех логических функций двузначной логики, обозначаем .

Тогда алгебра тоже будет булевой алгеброй (булевой алгеброй логических функций), так как для ее операций тоже выполняются соотношения 1-14, где вместо переменных и подставлены логические функции .

Если U – некоторое множество элементов мощности n: .

Определение: B - булеан U – это множество (совокупность) всех подмножеств множества U.

Определение: Алгебра (B,), несущим множеством которой является множество B, а операциями – пересечение, объединение и дополнение множеств, называется булевой алгеброй множества U или алгеброй Кантора. Ее тип (2,2,1).

Общий термин ”булева алгебра” для алгебр множеств и логических функций не случаен.

Определение: Всякая алгебра типа (2,2,1) называется булевой алгеброй, если ее операции удовлетворяют основным свойствам булевых операций 1-14.

В алгебре множеств элементами являются подмножества фиксированного (”универсального”) множества U, операции & соответствует пересечение , операции – объединение , операции (отрицание) соответствует дополнение; единицей является само множество U, нулем - . Справедливость соотношений 1-14 для алгебры множеств можно доказать непосредственно их проверкой. Для этого нужно рассмотреть переменные в них как множества, знаки & и заменить на и , и показать, что, если какой-либо элемент принадлежит множеству из левой части равенства, то он принадлежит и правой части, и наоборот.

В пункте 4.2. (в теореме о числе подмножеств конечного множества) отмечалось и использовалось взаимно однозначное соответствие между множеством двоичных векторов длины n и множеством B, где : каждому подмножеству соответствует двоичный вектор , где .

Булева алгебра на множестве (двоичных векторов) определяется следующим образом: для любых и

^.

Поскольку компоненты (разряды) и векторов и принимают значения 0 и 1, то указанные операции над компонентами – это просто логические операции над двоичными переменными.

Определение: Операции над векторами назовем покомпонентными (поразрядными) логическими операциями над двоичными векторами.

Такие операции (наряду с логическими операциями над переменными) входят, в частности, в систему команд любой современной ЭВМ. Выполнение их очень просто: вектор содержит единицы во всех разрядах, в которых есть 1 либо в , либо в ;

- вектор содержит единицы только в тех разрядах, в которых есть единицы и в , и в ;

- вектор содержит единицы в тех разрядах, в которых содержит 0 и наоборот.

Например:

, то = 11011, = 01010,

= 10100, .

Теорема 1(об изоморфизме булевых алгебр)

Если , то булева алгебра (B,) изоморфна булевой алгебре .

Доказательство:

Итак, вспомним взаимно однозначное соответствие между B и .

Множеству М B соответствует , т.е.

. (*)

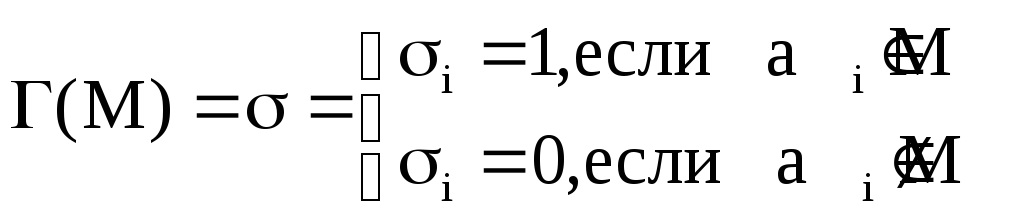Остается показать, что Г – изоморфизм, т.е. проверить выполнение равенства гомоморфизма алгебр для всех трех операций:

,

если .

Справедливость их вытекает из (*). Докажем, например второе:

- если , то i-ый разряд вектора равен 1;

но, с другой стороны, это означает, что или , но это (по гомоморфизму) означает, или , и, следовательно, i-ый разряд вектора равен 1;

- если , то i-ый разряд вектора равен 0;

но это означает, что и , но это (по Г) означает, и , и, следовательно, i-ый разряд вектора равен 0.

Аналогично доказываются остальные равенства.

Эта теорема позволяет заменить теоретико-множественные операции над системой подмножеств поразрядными логическими операциями над двоичными векторами. Такая замена часто используется при программировании, поскольку представление двоичных векторов и поразрядные операции над ними реализуются очень просто.

Рассмотрим теперь множество всех логических функций m переменных . Оно замкнуто относительно операций (результат их применения к функциям из снова дает функцию из , и, следовательно, образует конечную булеву алгебру , являющуюся подалгеброй булевой алгебры логических функций.

Теорема 2 (об изоморфизме булевых алгебр).

Если , то булева алгебра множеств (B,) изоморфна булевой алгебре функций .

Доказательство:

1. Прежде всего отметим, что эти алгебры равномощны и обе содержат по элементов т.к. если , то B=, и т.к. все двоичные функции с m переменным определяются вектор-столбцом с компонентами, то таких различных двоичных векторов будет ;

2. Поскольку все множества U одинаковой мощности порождают изоморфные булевы алгебры (B,) множеств, то эту теорему достаточно доказать для какого-либо конкретного U, удовлетворяющего условию . В качестве такого множества U возьмем множество– двоичных векторов длины m и, следовательно, будем доказывать изоморфизм между булевой алгеброй множеств (B,) и булевой алгеброй функций ;

3. Обозначим через множество единичных наборов функции f. Тогда набор принадлежит . Соответственно (гомоморфизм отображает f в множество единичных наборов ) – между функциями и их единичными множествами является взаимно однозначным соответствием между и B, поскольку различным функциям соответствуют различные множества, и наоборот.

Определение: Функцию f , единичным множеством которой служит М, называют характеристической функцией множества М.

4. Покажем, что взаимно однозначное соответствие Г является изоморфизмом. Достаточно проверить выполнение равенств гомоморфизма для всех трех пар операций, которое в данном случае сводится к трем уравнениям:

,

для любых функций f и g от m переменных. Докажем втрое из них.

Пусть ( - двоичный вектор, , f – единичное множество функции ), тогда и, следовательно, или и, значит, или , следовательно, .

Обратно:

или

или

.

Аналогично доказываем остальные свойства.

Замечание: Во избежание путаницы обращаем внимание на различие объектов в доказанных нами теоремах.

1. В теореме 1 фигурировала алгебра со следующим основным множеством:

- - множество произвольной природы и любой конечной мощности n;

- B - множество подмножеств U мощности ;

- - множество двоичных векторов длины n также мощности .

В теореме 2 участвовали:

- тот же множество , но с дополнительным условием (m – любое натуральное число);

- - конкретное множество U с этими же условиями: ;

- множество логических функций m переменных: ;

- B - множество подмножеств :B=.

2. Множества и , хотя и имеют одну и ту же природу (состоят из двоичных наборов), использовались в теореме 1 и теореме 2 по-разному. В теореме 1 была использована структура элементов , благодаря чему над ними оказались возможными поразрядные логические операции. Подмножества не рассматривались. В теореме 2 структура элементов не учитывалась, само было выбрано только для естественности и наглядности, зато рассматривалась B - система

Таблица 1

			f	g
0	0	0	0	0	0	0	1
0	0	1	1	1	1	1	0
0	1	0	0	1	1	0	1
0	1	1	0	0	0	0	1
1	0	0	1	0	1	0	0
1	0	1	1	1	1	1	0
1	1	0	0	0	0	0	1
1	1	1	0	1	1	1	1

подмножеств . Теоремы 1 и 2 указывают на тесную связь между множествами и логическими функциями и позволяют переходить от операций над множествами к операциям над функциями и обратно. В частности, они дают возможность непосредственно производить операции над функциями, заданными не формулами, а таблицами или единичными множествами.

Из теоремы 1 и теоремы 2 следует, что булевы операции над функциями, заданными таблицами, сводятся к поразрядным логическим операциям над столбцами значений функций. Пример, приведенный в таблице, содержащей две функции f и g, и результат булевых операций над ними.