8. Параллельные проекции.

Параллельное проецирование можно рассматривать как частный случай центрального проецирования, когда центр проецирования удален в бесконечность, а проецирующие лучи параллельные. Положение проецирующих прямых относительно плоскости проекций определяется вектором направления проецирования. Получаемое при этом изображение называют параллельной проекцией объекта.

При параллельном проецировании сохраняются свойства центрального и добавляются следующие:

1. проекции параллельных прямых параллельны между собой;

2. отношение отрезков прямой равно отношению их проекций;

3. отношение отрезков двух параллельных прямых равно отношению их проекций.

В свою очередь параллельные проекции подразделяются на прямоугольные, когда проецирующие лучи перпендикулярны плоскости проекций, и косоугольные, когда направление проецирования образует с плоскостью проекций угол не равный 90⁰.

Частным случаем параллельного проецирования является ортогональное проецирование. Проекция объекта, полученная с использованием этого метода, называется ортогональной. Ортогональному проецированию присущи все свойства параллельного и центрального проецирования и, кроме того, справедлива теорема о проецировании прямого угла: если хотя бы одна сторона прямого угла параллельна плоскости проекций, а вторая не перпендикулярна ей, то прямой угол на эту плоскость проецируется в прямой угол.

К проекционным изображениям в начертательной геометрии предъявляются следующие основные требования:

1. Обратимость – восстановление оригинала по его проекционным изображениям (чертежу) – возможность определять форму и размеры объекта, его положение и связь с окружающей средой.

2. Наглядность – чертеж должен создавать пространственное представление о форме предмета.

3. Точность – графические операции, выполненные на чертеже, должны давать достаточно точные результаты.

4. Простота – изображение должно быть простым по построению и допускать однозначное описание объекта в виде последовательности графических операций.

К счастью, эти требования распространяются не на все задачи компьютерной графики.

В машинной графике используют центральные (перспективные) и параллельные проекции.

В зависимости от взаимного положения плоскости проекции и координатных осей проекции делят на следующие виды.

Одноточечную центральную проекцию мы уже рассмотрели достаточно подробно. Далее эти наработки мы используем в качестве базы для изучения других видов проекций.

Начнем пояснения с наиболее простых видов проекции.

Ортографическая проекция – в общем случае, изображение какого-нибудь предмета на плоскости, посредством проецирования отдельных его точек при помощи перпендикуляров к этой плоскости. В этой проекции предметы представляются такими, какими они представлялись бы наблюдателю, смотрящему на них с бесконечного расстояния. Каждый план есть проекция местности на горизонтальную плоскость, проведенную через середину участка. В ортографической проекции иногда изображают и целые полушария земли.

В компьютерной графике при ортографической проекции плоскость проекции совпадает с одной из координатных плоскостей или параллельна ей. Например, матрица проецирования вдоль оси X на плоскость Y0Z имеет вид:

.

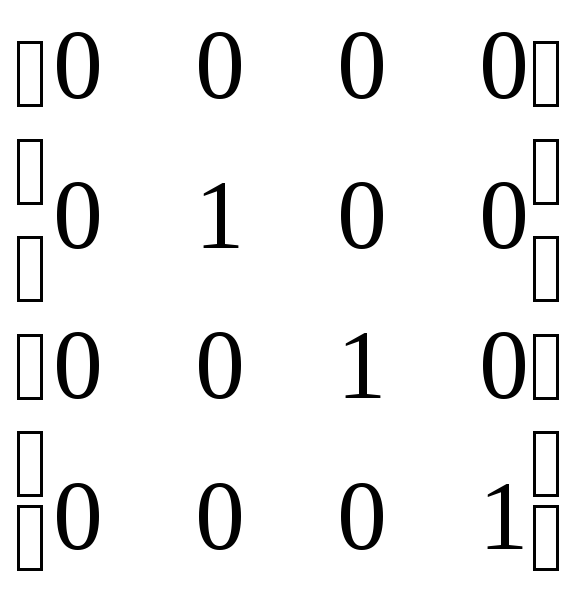Если плоскость проецирования параллельная плоскости Y0Z, то матрицу проецирования нужно умножить на матрицу переноса.

Тогда матрица проецирования вдоль оси X будет иметь вид:

.

Матрица проецирования вдоль оси Y имеет вид

.

Матрица проецирования вдоль оси Z имеет вид

.

Ортографическая проекция часто кажется немного странной, потому что объекты остаются того же самого размера, независимо от расстояния: это подобно просмотру сцены от отдаленной в бесконечность точки. Однако, ортонормированный просмотр очень полезен, потому что обеспечивает более «техническое» проникновение в сцену, делая ее проще для определения пропорций.

Обычно ортогональную проекцию применяют для детального рассмотрения объекта с шести разных сторон. Можно, например, рассмотреть дом снизу, сверху, спереди, сзади, слева и справа - при этом направление проецирования совпадает с одной из осей координат. Пока нет отсечения невидимых граней имеет смысл рассматривать только проекции параллельно трех осей координат.