4. Двумерные преобразования в декартовых координатах.

Операции преобразования – это пересчет координат. Точку удобно рассматривать как вектор, проложенный от начала координат в эту точку.

Преобразование вектора равносильно умножению вектора на матрицу. Преобразование точки с координатами (X,Y) в точку с координатами (X₁, Y₁) можно записать в аналитическом виде

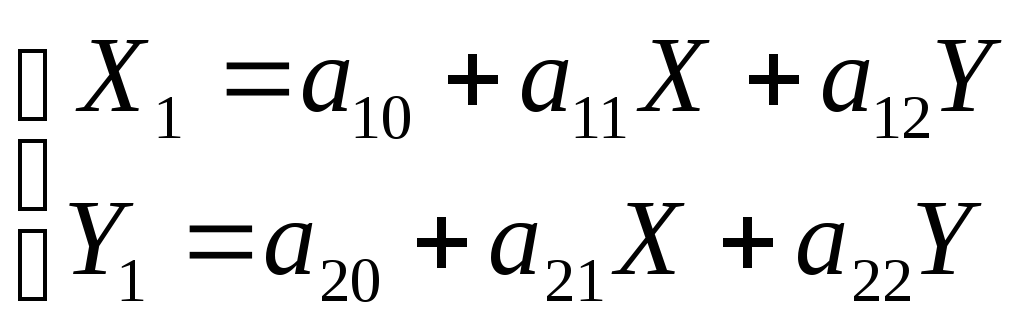
или в матричном виде:

.

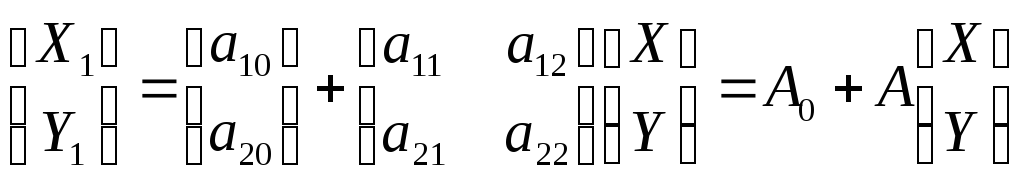Здесь выражение

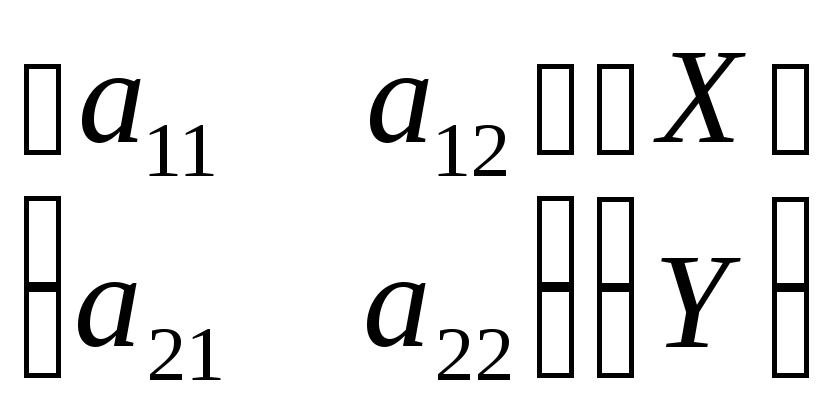
раскрывается в виде

.

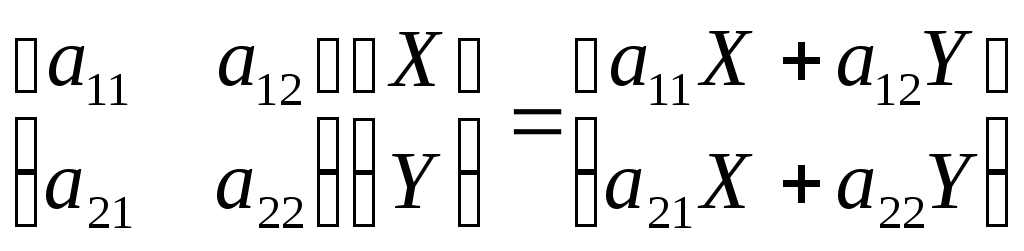Будем рассматривать только преобразования точки относительно начала координат или отдельной оси координат. Другие преобразования представляют собой последовательное применение этих преобразований.

Пусть на плоскости дана точка P(X,Y) (рис. 2). Например, X=9,Y=4.

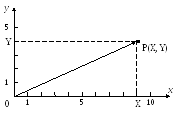
Рис. 2. Исходное расположение точки

Перенос (transfer) имеет вид:

,

или в векторной форме:

.

Результат преобразования изображен на рис. 3. Здесь .

Рис. 3. Перенос точки

Перенос задается вектором смещения . При переносе объекта форма объекта не изменяется.

Здесь и далее - для единообразия матричных преобразований точки обозначаем строковой формой вектора.

Масштабирование (scaling) имеет вид:

,

или в матричной форме:

,

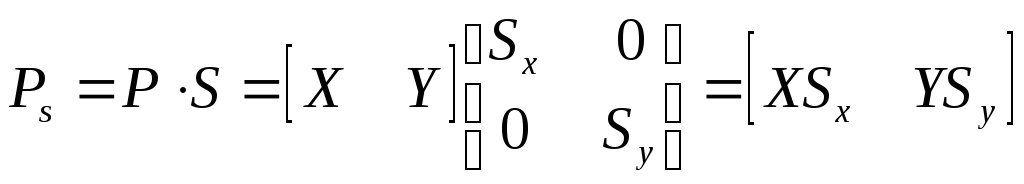где - коэффициенты масштабирования по осям, а 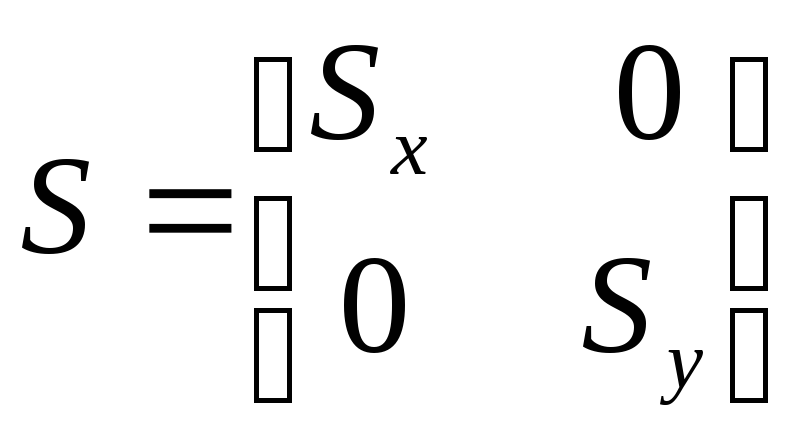- матрица масштабирования.

Рис. 4. Масштабирование

Поворот (rotation).

Пусть вектор нужно повернуть против хода часовой стрелки вокруг оси z на угол α.

Рис. 5. Пример поворота

Тогда новые координаты вычисляют по формулам:

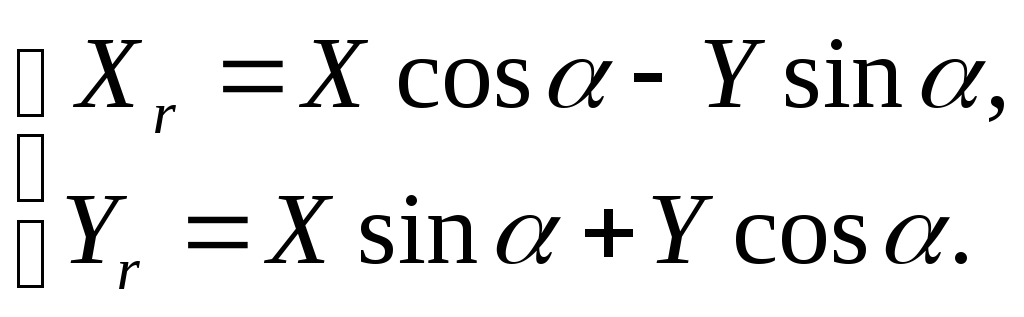
В матричной форме поворот записывают так:

.

Здесь - матрица поворота.

Матрица поворота всегда ортогональна. Геометрически это означает, что векторы-столбцы и векторы-строки этой матрицы имеют единичную длину и взаимно перпендикулярны. С точки зрения матричных вычислений эта матрица имеет следующие свойства:

.

То есть, для возврата точки в исходное положение достаточно умножить:

.

Это только один пример полезных свойств матричных вычислений.

5. Двумерные преобразования в однородных координатах.

Матричные вычисления позволяют отвлечься от множества деталей, упрощать внешний вид расчетных формул и проникать в глубинные свойства преобразований.

Но в декартовых координатах с помощью умножения на матрицу нельзя выполнить перенос.

Выгодно использовать однородные координаты.

Система координат, в которой представление точки в двухмерном (трехмерном) пространстве задается при помощи трех (четырех) координат (Р₁, Р₂, Р₃(, Р₄)), называется системой однородных координат. Обычно добавочную координату приводят к 1.

Двумерные однородные координаты точки имеют вид . Здесь w – произвольный ненулевой множитель.

Двумерные декартовые координаты точки получаются из однородных координат делением на множитель w:

.

В однородных координатах точка Р(X,Y) записывается как Р(w×x,w×y,w) для любого масштабного множителя w¹0.

Преобразования переноса, масштабирования и поворота в однородных координатах относительно центра координат все имеют одинаковую форму произведения вектора исходных координат на матрицу преобразования.

Перенос имеет матричную запись:

.

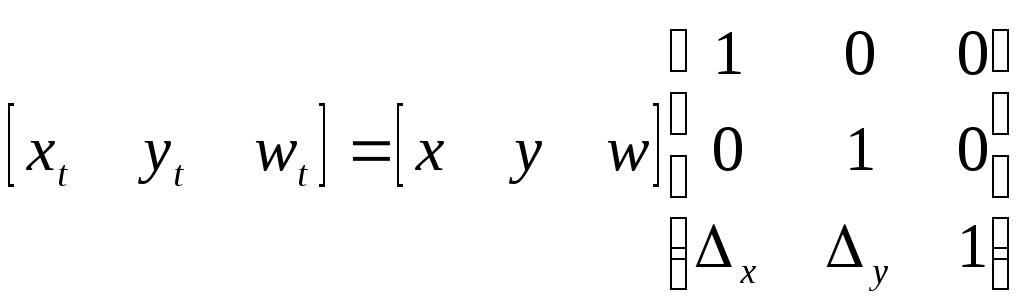Масштабирование имеет матричную запись:

.

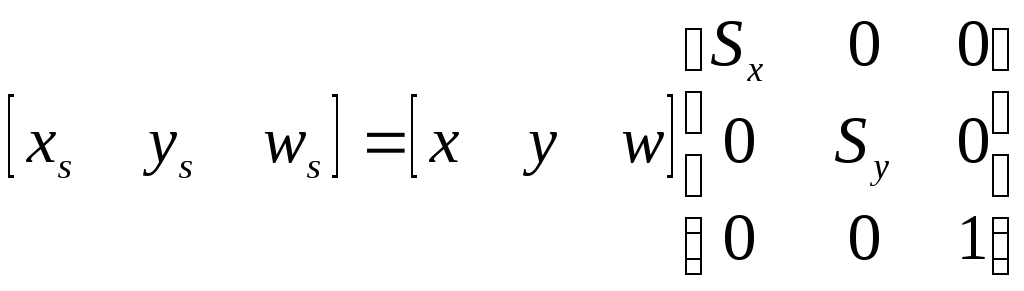Поворот имеет матричную запись:

.

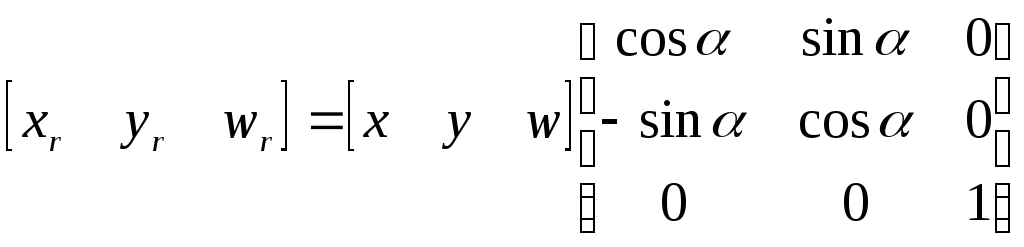Композиция преобразований

Последовательное выполнение нескольких преобразований можно представить в виде единой матрицы суммарного преобразования. Умножение на единственную матрицу, естественно, выполняется быстрее, чем последовательное умножение на несколько матриц.

Рассмотрим сдвиг точки P₀ на расстояние в точку P₁, а затем сдвинем точку P₁ на расстояние в точку P₂. Обозначая через T₁ и T₂ матрицы сдвига, получим:

.

Легко доказать, что последовательное выполнение двух сдвигов должно быть эквивалентно одному сдвигу на расстояние . Действительно, перемножив матрицы сдвига, легко получить, что:

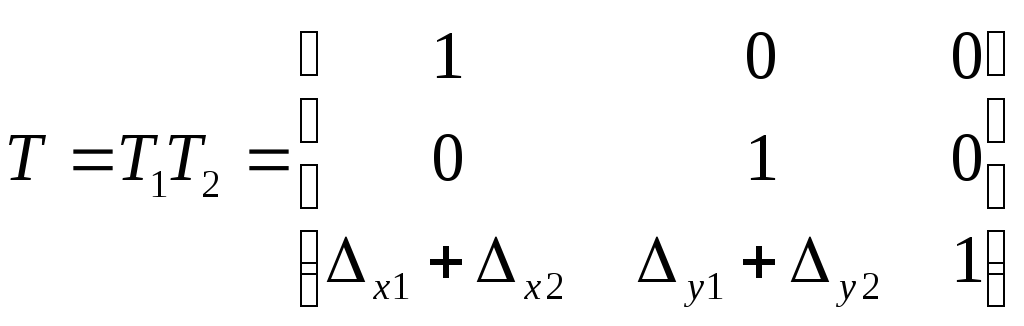
Рассмотрим теперь последовательное выполнение масштабирований, первое с коэффициентами (S_x1, S_y1), второе с коэффициентами (S_x2, S_y2). Легко показать, что суммарное масштабирование будет мультипликативным. Обозначая через S₁ и S₂ матрицы масштабирования, получим

.

Легко вычислить выражение для элементов матрицы S:

.

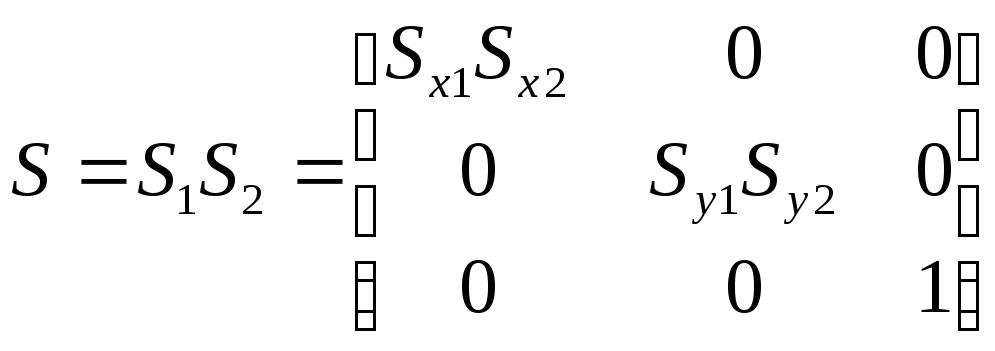Получили, что результирующее масштабирование мультипликативно.

Можно показать, что два последовательных поворота аддитивны. Пусть нужно выполнить поворот относительно начала координат сначала на угол α₁, затем на α₂. Тогда результирующая матрица поворота имеет вид:

.

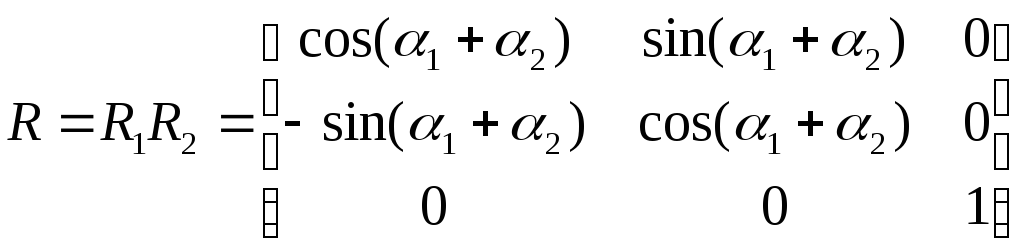Рассмотрим более сложные задачи.

Произведение нескольких матриц называют композицией.

Выполним, например, поворот точки P(X,Y) относительно некоторой произвольной точки (m,n) на угол α.

Так как мы умеем поворачивать лишь вокруг начала координат, разобьем исходную задачу на три подзадачи:

1) перенос начала координат в точку (m,n);

2) поворот на угол α;

3) обратный перенос, при котором точка (m,n) из начала координат возвращается в первоначальное положение.

Рассмотрим перенос точки (m,n) в начало координат. Эту задачу можно рассматривать и как перенос начала координат в точку (m,n). При этом точку, которую собираемся повернуть, нужно перенести на величину (-m,-n).

Матрица преобразования имеет вид

.

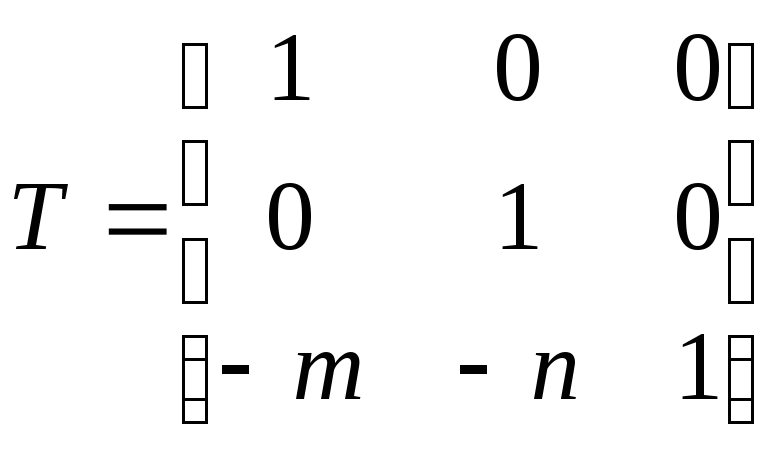Перенос точки P(X,Y) вычисляем как обычно:

.

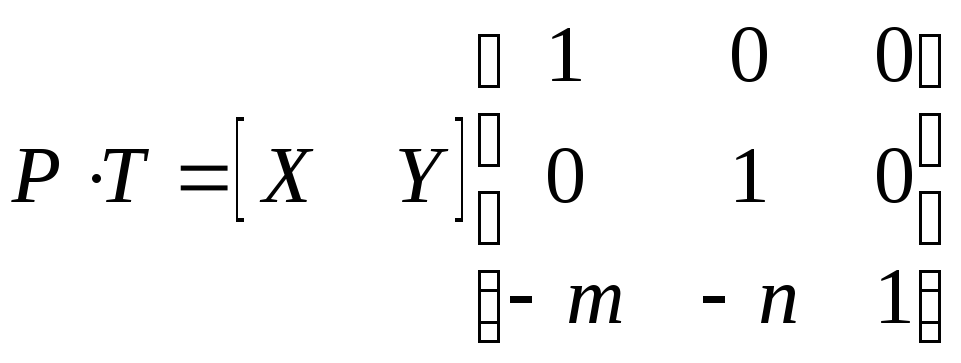Теперь поворачиваем точку на угол α:

.

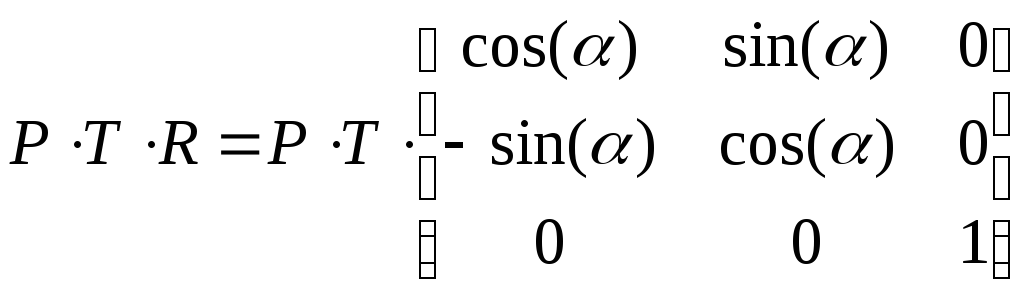Теперь вернем начало координат в исходное состояние – выполним перенос точки на величину (m,n).

.

Точка и есть результат поворота точки P(X,Y) относительно точки (m,n) на угол α.

Это было пошаговое пояснение решения сложной задачи. Все сложные преобразования приводятся к композиции ранее рассмотренных элементарных преобразований переноса, масштабирования и поворота.

Рассмотрим, как при этом используется композиция матриц.

Окончательный результат поворота точки P(X,Y) относительно точки (m,n) на угол α в виде матричных преобразований можно представить следующим образом:

.

Здесь - композиция матриц элементарных преобразований.

Представим теперь, что нужно повернуть треугольник вокруг точки (m,n) на угол α. Ясно, что достаточно повернуть только ключевые точки (три вершины), по которым затем можно изобразить повернутый треугольник.

Очевидно одно – нужно изначально вычислить произведение матриц.

Применение преобразования к вершинам треугольника P₁(X₁,Y₁), P₂(X₂,Y₂), P₃(X₃,Y₃) можно организовать по-разному.

Рассмотрим два варианта преобразований.

1. Можно последовательно применить ко всем вершинам:

.

2. Можно построить матрицу вершин треугольника

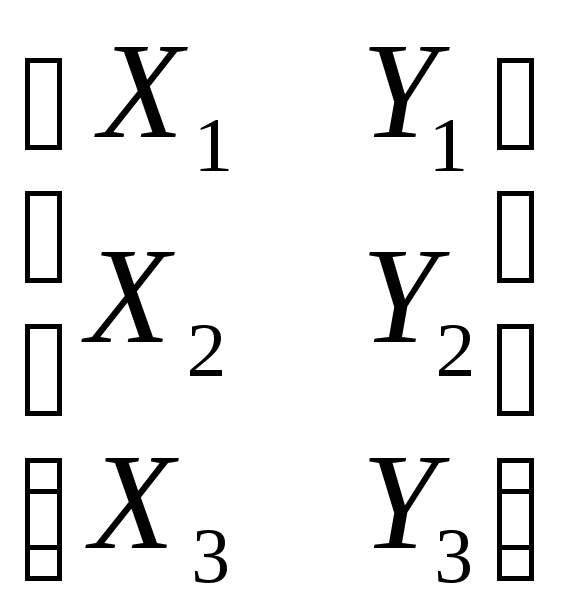
и справа умножить эту матрицу на матрицу преобразований M:

.

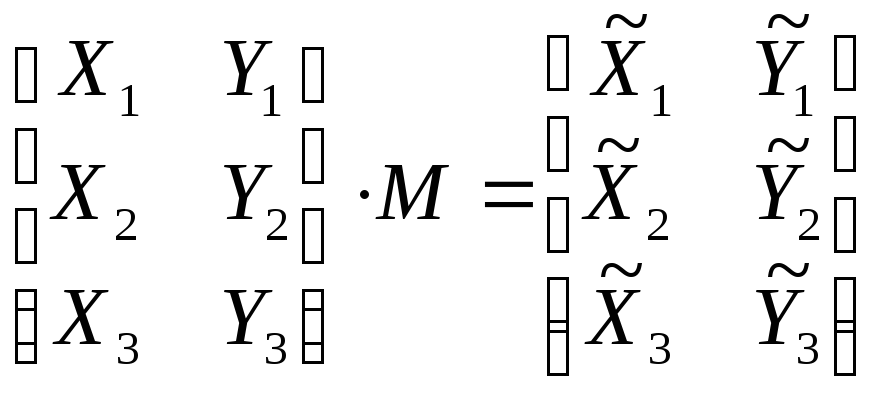Результат в обоих случаях будет один и тот же. Отличие заключается лишь в организации вычислительного процесса.