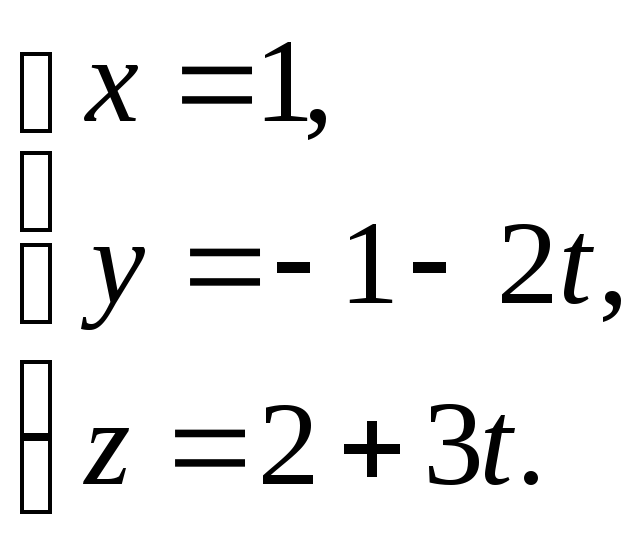3. Уравнения прямой в пространстве.
Понятие пространственной прямой связано с понятием плоскости. Например, прямой является линия пересечения двух плоскостей (аксиома стереометрии). Рассмотрим способы описания прямой.
Способ 1. Общее уравнение прямой представляет собой систему из двух уравнений пересекающихся плоскостей:
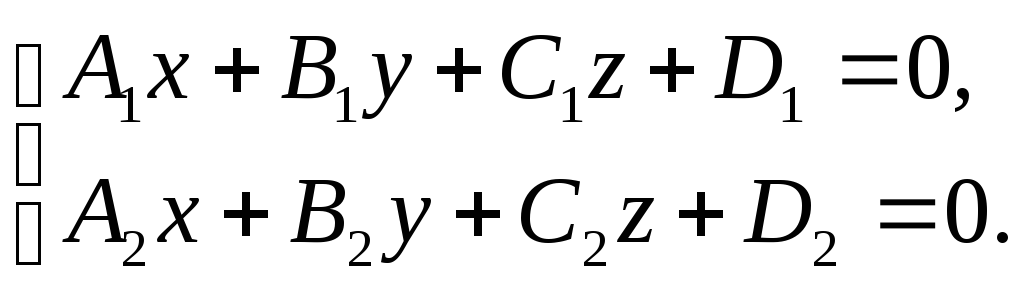
Способ 2. Через
точку
можно построить прямую параллельно
некоторому вектору
.
В этом случае уравнение называется
каноническим
и имеет вид:
и является условием коллинеарности двух векторов:
Если направляющий
вектор
перпендикулярен какой-либо координатной
оси, то соответствующая координата
вектора равна нулю. Запись канонического
уравнения является символической, и
деление на ноль не требуется.
Началом вектора
является известная
по условию точка
искомой прямой L,
а концом - произвольная точка
этой прямой.
По этому же способу
можно построить каноническое уравнение
прямой, проходящей через две заданные
точки
и
.
Для этого в предыдущем построении
достаточно принять
или, что то
же самое,
.
В итоге получим:
.
Переход от общих уравнений к каноническим требует некоторого усилия. Рассмотрим идею такого перехода. Параметры системы уравнений
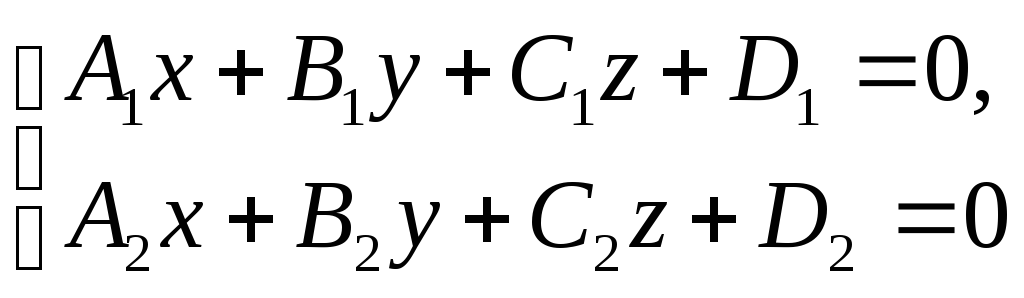
представляют собой
два вектора
и
,
перпендикулярных к обеим плоскостям.
Очевидно, что векторы
и
перпендикулярны и прямой, лежащей на
пересечении этих плоскостей. Найдем
вектор
,
который перпендикулярен векторам
и
.
Самый простой способ – это построить
их векторное произведение
:
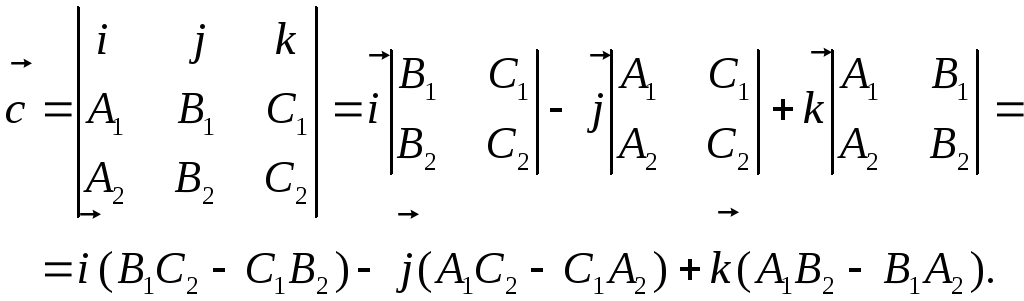
Отсюда вытекает:
.
Найдем точку
,
через которую проходит прямая. Очевидно,
что эта точка должна лежать на пересечении
плоскостей. Поэтому запишем:
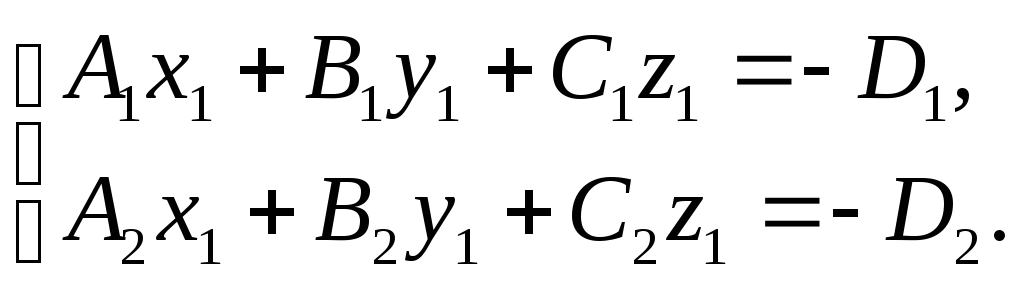
Для определения
трех неизвестных
имеем всего два уравнения. Здесь можно
поступить следующим простым способом.
-
Принять
и решить систему
Если решение существует, то точка найдена. Иначе, переходим в пункт 2.
-
Принять
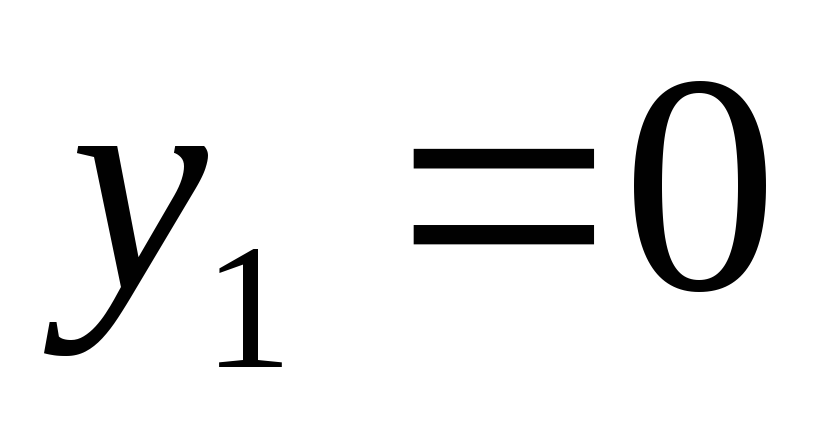и решить систему
Если решение существует, то точка найдена. Иначе, переходим в пункт 3.
-
Принять
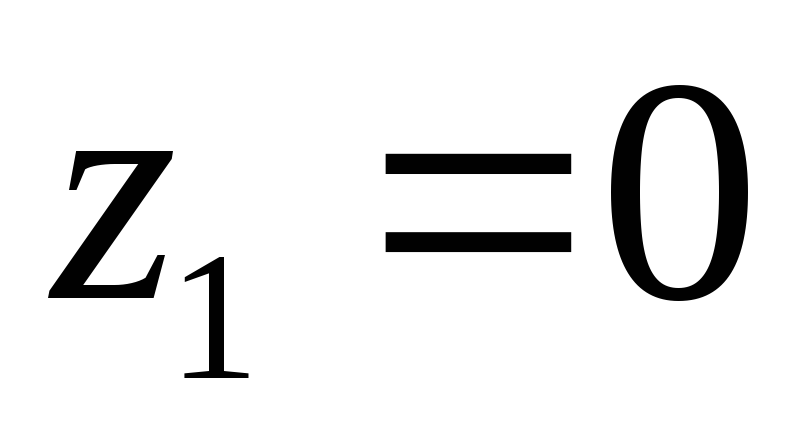и решить систему
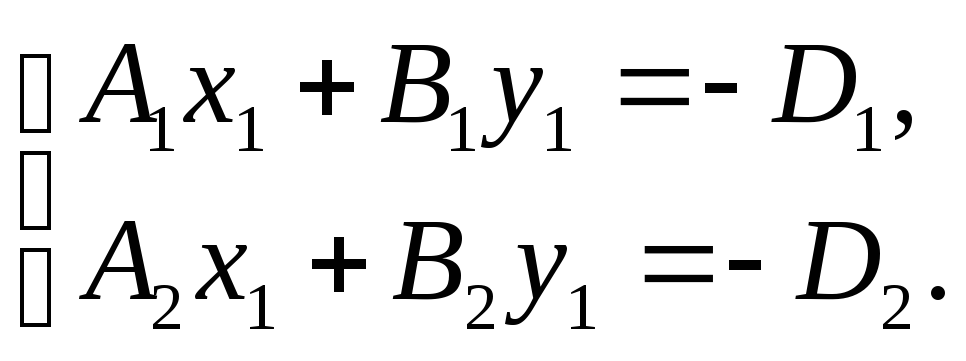
Если решение существует, то точка найдена. Иначе, искомая прямая не существует, например, исходные плоскости не пересекаются.
Из канонического уравнения можно получить параметрическое уравнение прямой, приравнивая каждую дробь в отдельности некоему параметру t. Затем из этих трех равенств выражают координаты (x,y,z) точек описываемой прямой:
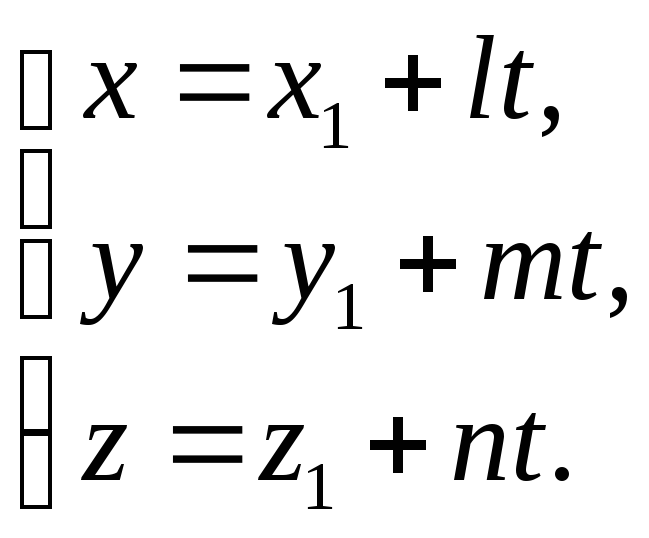
Пример.
Записать
канонические уравнения прямой, проходящей
через точку М(1;-1;2)
параллельно вектору
.
Видим, что вектор
перпендикулярен координатной оси Ox.
Канонические уравнения искомой прямой имеют вид:
.
Здесь запись нуля в знаменателе считается допустимой, так как это символическая запись. Получим общие уравнения прямой:
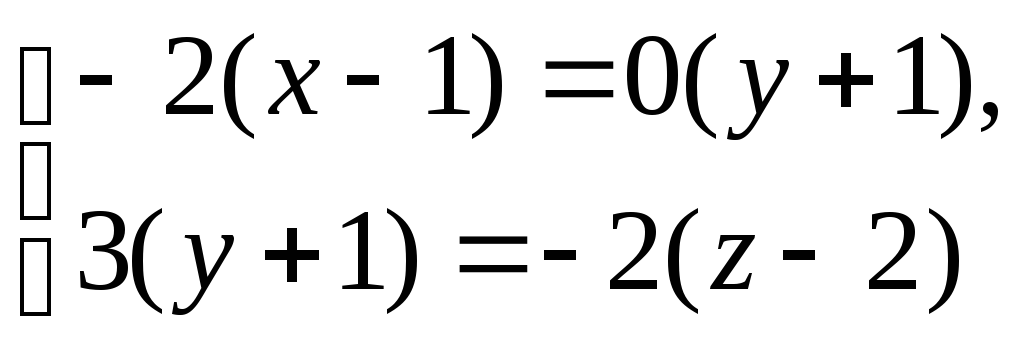
или
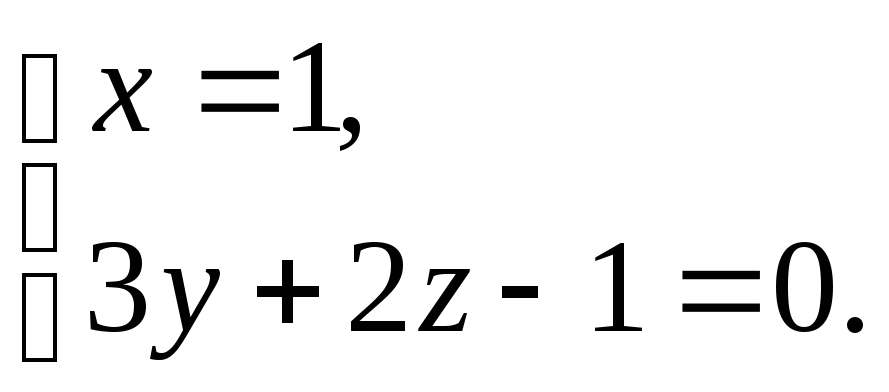
По
сути, это уравнение прямой
,
лежащей на плоскости x=1.
Параметрические уравнения этой прямой имеют вид:
