Метод «Контрольные Карты»

Контрольные карты (КК) - инструмент, позволяющий отслеживать ход процесса и воздействовать на него (с помощью соответствующей обратной связи), предупреждая его отклонения от предъявляемых к процессу требований.

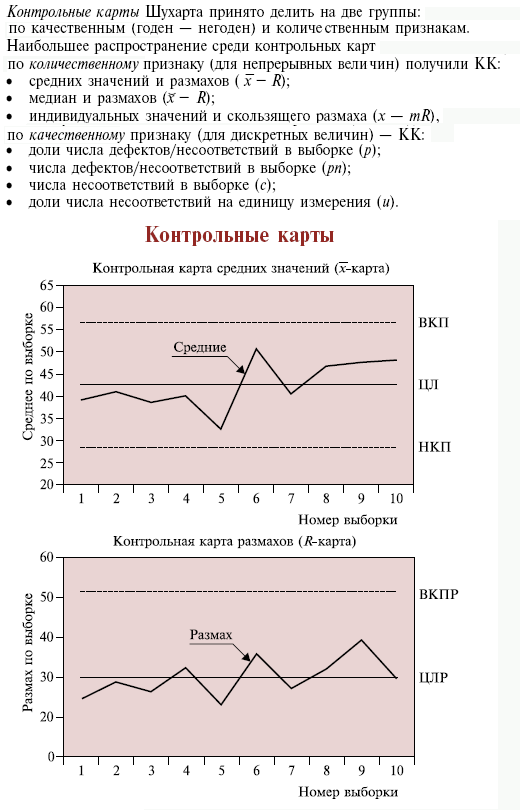
Правила построения контрольных карт

При построении КК на оси ординат откладываются значения контролируемого параметра, а на оси абсцисс - время t взятия выборки (или ее номер).

КК состоит обычно из трех линий. Центральная линия (ЦЛ) представляет собой требуемое среднее значение характеристики контролируемого параметра качества. Так, в случае (`x - R)-карты это будут номинальные значения `x и R, нанесенные на соответствующие карты.

Две другие линии, одна из которых находится над центральной - верхний контрольный предел (ВКП), а другая под ней - нижний контрольный предел (НКП), представляют собой максимально допустимые пределы изменения значений контролируемой характеристики (показателя качества).

Дополнительная информация:

• Любая, пусть первоначально неэффективная КК, - необходимое средство для наведения порядка в контроле технологического процесса.

• Для успешного внедрения на практике КК важно не только овладеть техникой их составления и ведения, но, что значительно важнее, научиться правильно "читать" карту.

Достоинства метода

• Указывает на наличие потенциальных проблем до того, как начнется выпуск дефектной продукции.

• Позволяет улучшить показатели качества и снизить затраты на его обеспечение.

Недостатки метода

Грамотное построение КК представляет собой сложную задачу и требует определенных знаний.

Ожидаемый результат

Получение объективной информации для принятия решений об эффективности процесса.

Расчетная часть

Упорядочение первичной статистической совокупности

Преобразование данных в группированный статистический ряд (где частота равна отношению количества данных, попавших в интервал, к общему количеству).

разряд	частота
25,98245-25,98427	0,045
25,98427-25,98608	0,065
25,98608-25,9879	0,065
25,9879-25,98971	0,065
25,98971-25,99152	0,055
25,99152-25,99334	0,07
25,99334-25,99515	0,085
25,99515-25,99697	0,1
25,99697-25,99878	0,115
25,99878-26,0006	0,105
26,0006-26,00241	0,09
26,00241-26,00423	0,08
26,00423-26,00604	0,06

Построение гистограммы.

Рис. 6 Гистограмма

Гистограмма представляет собой гребенку (мультимодальный тип). Классы через один имеют более низкие частоты. Такая форма встречается, когда число единичных наблюдений, попадающих в класс, колеблется от класса к классу или когда действует определенное правило округления данных.

Математическое ожидание отклонения μ равно среднему арифметическому .

μ = 26 мм

мкм

Вероятная доля дефектной продукции

Р_деф = .

Учитывая что Т_верх= D₀+ES = 26-0,005 = 25,995 мм; Т_ниж= D₀+EI= 26-0,019 = 25,981 мм, а также с учетом принятой настройки измерительной скобы на размер 25,980 мм получаем

Индекс воспроизводимости процесса

Вероятностная проверка на вид закона распределения

Принимаем основную гипотезу Н₀, что данные распределены по нормальному закону.

Н1 – альтернативная гипотеза (данные распределены не по нормальному закону).

интервал	Ф()	Ф()	P
25,98245-25,98427	-0,91814	-0,95764	0,01975
25,98427-25,98608	-0,85294	-0,91814	0,0326
25,98608-25,9879	-0,75395	-0,85294	0,049495
25,9879-25,98971	-0,62114	-0,75395	0,066405
25,98971-25,99152	-0,44481	-0,62114	0,088165
25,99152-25,99334	-0,23582	-0,44481	0,104495
25,99334-25,99515	-0,00798	-0,23582	0,11392
25,99515-25,99697	0,22052	-0,00798	0,11425
25,99697-25,99878	0,42452	0,22052	0,102
25,99878-26,0006	0,60468	0,42452	0,09008
26,0006-26,00241	0,74571	0,60468	0,070515
26,00241-26,00423	0,84728	0,74571	0,050785
26,00423-26,00604	0,91457	0,84728	0,033645

где Р = Ф() - Ф().

= 14,93

Зададимся уровнем значимости α = 0,01.

Тогда χ²_теор(10;0,01)=23,21.

χ²_расч< χ²_теор, значит гипотеза Н₀ подтверждается, следовательно, данные распределены по нормальному закону.

Построение контрольных карт

Построение контрольных карт производится в компьютерной среде Matlab.

Для решения используется матрица данных data, основанная на данных выборок. Уровень значимости α=0,01; объем выборки n=5.

Контрольная карта средних арифметических значений (Х-карта)

Исходные данные

>> data=[25.99697 25.98427 25.9879 26.00423 25.99697

25.98245 26.00423 25.99334 26.00241 25.99878

26.0006 26.0006 25.98427 25.99334 25.99697

26.0006 26.00423 25.99152 25.99878 25.99515

25.99697 25.99878 25.99515 26.00604 25.99152

25.99878 26.0006 25.99878 26.00423 26.0006

26.00604 25.99878 26.00423 25.99334 25.98427

26.0006 26.00423 26.0006 25.99878 25.99878

25.99878 25.99152 25.99878 26.00241 25.99515

26.00423 25.99697 25.99515 26.0006 25.99334

25.99515 25.99878 26.00423 25.99697 26.00241

26.00241 26.00241 25.98971 25.98608 26.00241

25.9879 25.99334 25.98427 25.98427 25.98608

25.99334 25.9879 25.98427 25.9879 25.98608

25.99334 25.98608 25.99515 25.9879 25.99334

25.99697 25.99697 25.98971 25.99515 25.98427

25.98608 25.99152 25.98971 25.99152 26.0006

25.99334 25.9879 25.98971 25.99515 26.00241

25.98608 26.0006 25.99697 25.98971 25.99697

25.99697 25.98971 26.00241 25.99697 25.9879

];

>> d=reshape(data,1,100);

>>alfa=0.01;

>> n=5;

Вектор выборочных средних

>>vx=mean(data)

vx=

Columns 1 through 5

25.9941 25.9962 25.9952 25.9981 25.9977

Columns 6 through 10

26.0006 25.9973 26.0006 25.9973 25.9981

Columns 11 through 15

25.9951 25.9966 25.9872 25.9879 25.9912

Columns 16 through 20

25.9926 25.9919 25.9937 25.9941 25.9948

Среднее по всем данным, принимаемое за

>> muo=mean(vx)

muo =

25.9950

Стандартное отклонение по всем данным

>> sigma=std(d)

sigma =

0.0063

Нижняя граница регулирования

>> a1=muo-sigma*norminv(1-alfa/2)/n^0.5

a1 =

25.9878

Верхняя граница регулирования

>> a2=muo+sigma*norminv(1-alfa/2)/n^0.5

a2 =

26.0023

Построение контрольной карты

>> x=1:20;

>> plot(x,vx,'*',x,vx,[1,20],[a1,a1],[1,20],[a2,a2])

>> grid

выборочное среднее, мкм

номер выборки

Рис.7 Контрольная карта среднего значения

Контрольная карта средних квадратических значений (S-карта)

Исходные данные такие же, как при построении Х-карты.

Вектор выборочных СКО

>> vs=std(data)

vs =

Columns 1 through 5

0.0080 0.0088 0.0068 0.0049 0.0054

Columns 6 through 10

0.0022 0.0088 0.0022 0.0041 0.0044

Columns 11 through 15

0.0038 0.0081 0.0038 0.0034 0.0039

Columns 16 through 20

0.0055 0.0054 0.0056 0.0060 0.0059

Стандартное отклонение по всем данным

>> sigma=std(d)

sigma =

0.0063

Граница регулирования

>> s1=sigma*((chi2inv(1-alfa,n))/n)^0.5

s1 =

0.0109

Построение контрольной карты

>> x=1:20;

>> plot(x,vs,'*',x,vs,[1,20],[s1,s1])

>> grid

выборочное отклонение

номер выборки

Рис.8 Контрольная карта среднеквадратических отклонений