7.Неперервні випадкові величини. Література : [2] стор. 87-106

[4] стор. 78-92, 103-110

7.1 У задачі 1-25 випадкова величина задана інтегральною функцією розподілу ймовірності F(x). Потрібно :

1) знайти диференціальну функцію (щільність ймовірності) f(x);

2) знайти ймовірність того, що випадкова величина X прийме значення які належать інтервалу ( ; );

3) побудувати графіки функцій F(x) і f(x);

4) знайти математичне сподівання M(x), дисперсію D(x), середнє квадратичне відхилення (x) випадкової величини X;

5) знайти моду ; 6) знайти медіану .

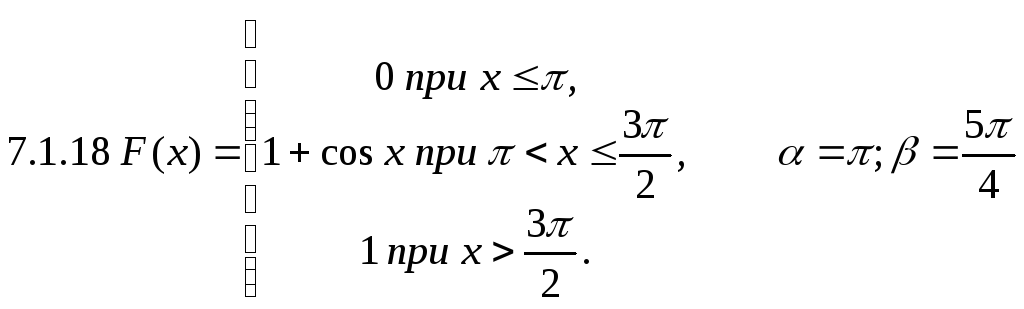
7.2.1. Випадкова величина Х, щільність якої , задана своєю функцією розподілу F(x) :

Потрібно:

а) знайти, математичне сподівання , дисперсію , моду і медіану

б) побудувати графіки функцій F(x) i і знайти ймовірність того, що 1/2<X<2.

7.2.2. Випадкова величина Х, щільність якої , задана своєю функцією розподілу F(x) :

Потрібно:

а) знайти, математичне сподівання , дисперсію , моду і медіану

б) побудувати графіки функцій F(x) i і ізнайти ймовірність того, що –3,5<X<4,5.

7.2.3. Випадкова величина Х, щільність якої , задана своєю функцією розподілу F(x) :

Потрібно:

а) знайти, математичне сподівання , дисперсію , моду і медіану

б) побудувати графіки функцій F(x) i і ізнайти ймовірність того, що 1<X<5.

7.2.4. Випадкова величина Х, щільність якої , задана своєю функцією розподілу F(x) :

Потрібно:

а) знайти, математичне сподівання , дисперсію , моду і медіану

б) побудувати графіки функцій F(x) i і ізнайти ймовірність того, що 0<X<5.

7.2.5. Випадкова величина Х, щільність якої , задана своєю функцією розподілу F(x) :

Потрібно:

а) знайти, математичне сподівання , дисперсію , моду і медіану

б) побудувати графіки функцій F(x) i і ізнайти ймовірність того, що <X<.

7.2.6. Випадкова величина Х, щільність якої , задана своєю функцією розподілу F(x) :

Потрібно:

а) знайти, математичне сподівання , дисперсію , моду і медіану

б) побудувати графіки функцій F(x) i і ізнайти ймовірність того, що <X<.

7.2.7. Випадкова величина Х, щільність якої , задана своєю функцією розподілу F(x) :

Потрібно:

а) знайти, математичне сподівання , дисперсію , моду і медіану

б) побудувати графіки функцій F(x) i і ізнайти ймовірність того, що 0<X<.

7.2.8. Випадкова величина Х, щільність якої , задана своєю функцією розподілу F(x) :

Потрібно:

а) знайти, математичне сподівання , дисперсію , моду і медіану

б) побудувати графіки функцій F(x) i і ізнайти ймовірність того, що 0<X<.

7.2.9. Випадкова величина Х, щільність якої , задана своєю функцією розподілу F(x) :

Потрібно:

а) знайти, математичне сподівання , дисперсію , моду і медіану

б) побудувати графіки функцій F(x) i і ізнайти ймовірність того, що -4<X<1.

7.2.10. Випадкова величина Х, щільність якої , задана своєю функцією розподілу F(x) :

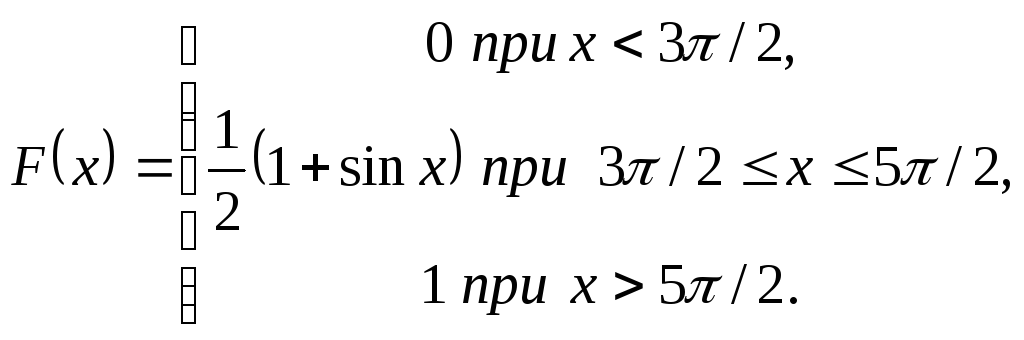
Потрібно:

а) знайти, математичне сподівання , дисперсію , моду і медіану

б) побудувати графіки функцій F(x) i і ізнайти ймовірність того, що 0<X<.

7.2.11. Випадкова величина Х, щільність якої , задана своєю функцією розподілу F(x) :

Потрібно:

а) знайти, математичне сподівання , дисперсію , моду і медіану

б) побудувати графіки функцій F(x) i і ізнайти ймовірність того, що 0<X<.

7.2.12. Випадкова величина Х, щільність якої , задана своєю функцією розподілу F(x) :

Потрібно:

а) знайти, математичне сподівання , дисперсію , моду і медіану

б) побудувати графіки функцій F(x) i і ізнайти ймовірність того, що 1<X<5.

7.2.13. Випадкова величина Х, щільність якої , задана своєю функцією розподілу F(x) :

Потрібно:

а) знайти, математичне сподівання , дисперсію , моду і медіану

б) побудувати графіки функцій F(x) i і ізнайти ймовірність того, що 1<X<3.

7.2.14. Випадкова величина Х, щільність якої , задана своєю функцією розподілу F(x) :

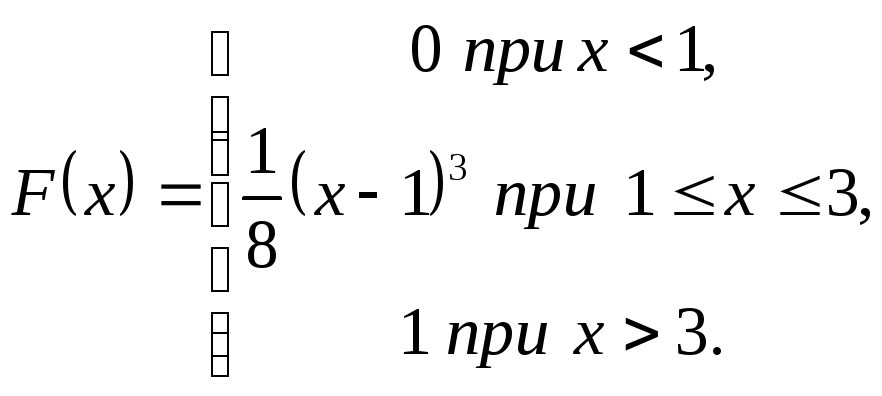
Потрібно:

а) знайти, математичне сподівання , дисперсію , моду і медіану

б) побудувати графіки функцій F(x) i і ізнайти ймовірність того, що 1,5<X<5.

7.2.15. Випадкова величина Х, щільність якої , задана своєю функцією розподілу F(x) :

Потрібно:

а) знайти, математичне сподівання , дисперсію , моду і медіану

б) побудувати графіки функцій F(x) i і ізнайти ймовірність того, що 1<X<3.

7.2.16. Випадкова величина Х, щільність якої , задана своєю функцією розподілу F(x) :

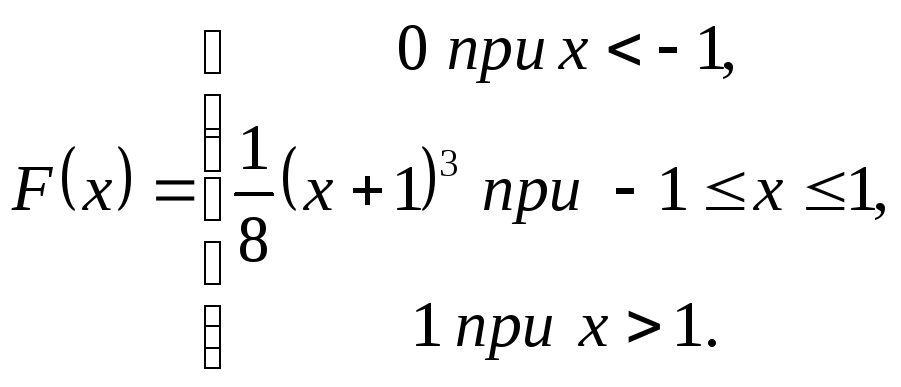
Потрібно:

а) знайти, математичне сподівання , дисперсію , моду і медіану

б) побудувати графіки функцій F(x) i і ізнайти ймовірність того, що 0.<X<5.

7.2.17. Випадкова величина Х, щільність якої , задана своєю функцією розподілу F(x) :

Потрібно:

а) знайти, математичне сподівання , дисперсію , моду і медіану

б) побудувати графіки функцій F(x) i і ізнайти ймовірність того, що -1<X<2.

7.2.18.Задана випадкова величина Х, щільність якої :

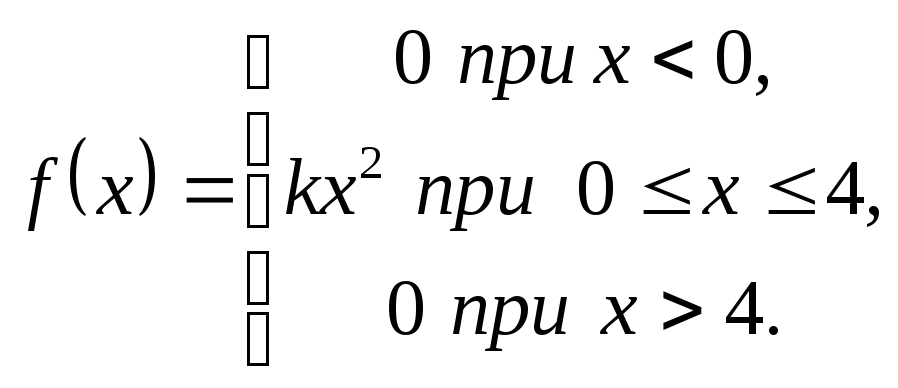
Потрібно:

а)знайти F( x), математичне сподівання , дисперсію , моду і медіану

б) побудувати графіки функцій F(x) i і ізнайти ймовірність того, що 2<X<5.

7.2.19.Задана випадкова величина Х, щільність якої :

Потрібно:

а) знайти, F( x), математичне сподівання , дисперсію , моду і медіану

б) побудувати графіки функцій F(x) i і ізнайти ймовірність того, що <X<.

7.2.20.Задана випадкова величина Х, щільність якої :

Потрібно:

а) знайти F( x), математичне сподівання , дисперсію , моду і медіану

б) побудувати графіки функцій F(x) i і ізнайти ймовірність того, що 0<X<2.

7.2.21.Задана випадкова величина Х, щільність якої :

Потрібно:

а) знайти F( x), математичне сподівання , дисперсію , моду і медіану

б) побудувати графіки функцій F(x) i і ізнайти ймовірність того, що 2<X<5.

7.2.22.Задана випадкова величина Х, щільність якої :

Потрібно:

а) знайти F( x), математичне сподівання , дисперсію , моду і медіану

б) побудувати графіки функцій F(x) i і ізнайти ймовірність того, що <X<.

7.2.23..Задана випадкова величина Х, щільність якої :

Потрібно:

а) знайти F( x), математичне сподівання , дисперсію , моду і медіану

б) побудувати графіки функцій F(x) i і ізнайти ймовірність того, що e/2<X<4.

7.2.24. .Задана випадкова величина Х, щільність якої :

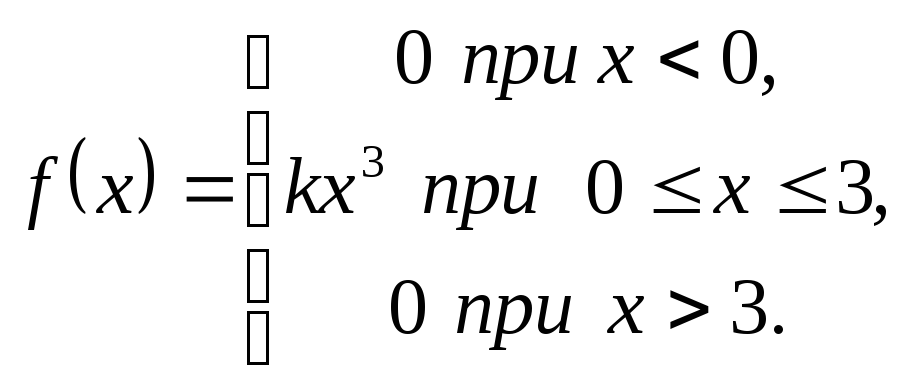
Потрібно:

а) знайти F( x), математичне сподівання , дисперсію , моду і медіану

б) побудувати графіки функцій F(x) i і ізнайти ймовірність того, що 2<X<5.

7.2.25..Задана випадкова величина Х, щільність якої , задана своєю функцією розподілу F(x) :

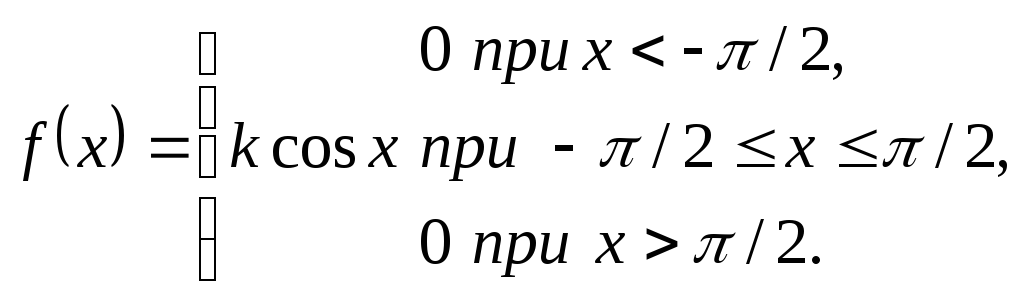
Потрібно:

а) знайти F( x), математичне сподівання , дисперсію , моду і медіану

б) побудувати графіки функцій F(x) i і ізнайти ймовірність того, що <X<.