2. Методы планирования работы систем с одним обслуживающим прибором

Пусть конечный поток требований N={1,2,3,...,n}, поступающих на обслуживание в заданные моменты времени, обслуживается одним прибором. В каждый момент времени прибор обслуживает не более одного требования. Требование k, поступает на обслуживание в момент времени d_k>=0 и для обслуживания требует t_k единиц времени. Порядок обслуживания может быть произвольным, либо регламентироваться заданными отношениями частичного порядка. При некоторых постановках задачи могут допускаться прерывания в обслуживании каждого отдельного требования. Необходимо так организовать процесс обслуживания, чтобы он в том или ином смысле был наилучшим.

Процесс обслуживания может быть описан заданием кусочно-постоянной, непрерывной слева функции s =s (t), принимающей при 0 t одно из значений 0, 1, 2,..., n. Если s(t)=k0, то в момент времени t прибор обслуживает требование k; если s (t) = 0, то в момент времени t ни одно из требований не обслуживается. Эта функция называется расписанием.

Расписание должно удовлетворять определенным условиям, вытекающим из самой постановки задачи. В качестве основных могут быть выделены :

• условие полноты: для любого 1 k n существует 0 < t < , такое, что s (t)=k; суммарная длина промежутков, на которых s (t) = k, равна t_k;

• условие готовности к обслуживанию: s(t) k для всех t<d_k;

• условие упорядоченности: если по условию задачи требование i необходимо обслужить раньше требования j и s (t') == i, то s (t)  j для всех t < t';

• условие непрерывности: если по условию задачи прерывания в обслуживании требований не допускаются и s {t') == s (t") = k  0, то s (t) == k для всех t' < t < t".

Расписания s =s (t), которые удовлетворяют перечисленным условиям, называются допустимыми.

Определенный практический интерес представляют расписания, которые удовлетворяют некоторым дополнительным условиям таким, как условия, связанные с необходимостью переналадок обслуживающего прибора, условия группирования требований при их обслуживании и т.п.

При рассмотрении задач такого рода под допустимым расписанием будем понимать такое расписание s=s(t), которое удовлетворяет всем требованиям, вытекающим из постановки конкретно рассматриваемой задачи.

Каждому допустимому расписанию s = s (t) соответствует вектор времен завершения обслуживания требований при этом расписании. Значение , , таковы что и s(t)k для всех t>.

Предполагается, что качество расписания s определяется вектором , т.е. каждому расписанию s ставится в соответствие значение некоторой скалярной функции F() вектора , определяемого расписанием s. Наиболее распространенным является следующий способ задания F(). Для каждого требования задается неубывающая кусочно-непрерывная функция _k(x), выражающая в количественном отношении «штраф», который необходимо «заплатить», если обслуживание этого требования завершится в момент времени х. В качестве F() выбирается одна из функций или . Функции _k(x) называются функциями штрафа. Расписание, которое удовлетворяет всем условиям рассматриваемой задачи, называется оптимальным, если ему соответствует наименьшее значение F().

Если прерывания обслуживания каждого отдельного требования запрещены, то активное расписание однозначно определяется заданием последовательности =(i₁, i₂,i₃ . . ., i_n), в которой эти требования обслуживаются. Таким образом, решение задачи может быть получено в результате рассмотрения конечного числа расписаний, определяемых возможными последовательностями обслуживания требований. Такие расписания называются перестановочными. Если множество N не упорядочено, то число перестановочных расписаний n!.

В общем случае, если допустимы прерывания процесса обслуживания требований, можно показать, что оптимальное расписание также может быть получено в результате рассмотрения конечного числа расписаний. Однако для однозначного описания этих расписаний уже недостаточно простого задания последовательности обслуживания требований. Необходимо указать, в какие моменты времени прерывается, а затем возобновляется процесс обслуживания каждого требования.

Рассмотрим весьма простые методы решения задачи оптимального упорядочения требований для некоторых частных случаев функций штрафа. Пред­полагается, что множество N требований не упорядочено, критерий опти­мальности расписания — суммарный штраф.

Пусть требования i и j обслуживаются непосред­ственно друг за другом и их обслуживание начинается в момент времени t  0. Если при этом первым обслужи­вается требование i, то суммарный штраф за обслужива­ние этих требований

Если первым обслуживается требование j, то суммарный штраф за обслуживание этих двух требований

Определим

Величина R_ij (t) показывает, насколько изменяется суммарный штраф при переходе от последовательности, при которой требование i начинало обслуживаться в мо­мент времени t непосредственно перед требованием j, к последовательности, отличающейся от исходной транс­позицией элементов i и j.

Если R_ij(t)<0, то при решении вопроса, какое именно из двух последовательно обслуживаемых требова­ний i и j необходимо начать обслуживать в момент вре­мени t, предпочтение следует отдать требованию i. Ана­логично, если R_ij {t)>0, то первым в момент времени t следует обслуживать требование j. Наконец, если R_ij {t)=0, то порядок обслуживания этих требований безразличен.

Поскольку функции _i(x) и _j(x) предполагаются кусочно-непрерывными в интервале (0, ), то этот интервал может быть разбит на конечное число интерва­лов, в каждом из которых величина R_ij(t) положительна. отрицательна или равна нулю.

Интервал (₁, ₂) называется интервалом очередности типа i  j, если R_ij(t)<0 для всех t(₁, ₂). Eсли R_ij(t)>0 для всех t(₁, ₂) интервал (₁, ₂) называется интервалом очередности типа j  i. При R_ij(t)=0 для всех t(₁, ₂) порядок обслуживания требований безразличен.

Величина R_ij(t) по определению зависит от значений t, t_i, t_j и функций штрафа _i(x) и _j(x). В каждом конкретном случае в результате несложных преобразований могут быть выделены интервалы очередности.

Задание интервалов очередности оказывается весьма полезным при поиске оптимальных расписаний методом последовательного конструирования вариантов.

Директивным сроком называется момент времени D_k>0, к которому необходимо или, во всяком случае, желательно завершить обслуживание требования . В общем случае не удастся построить такого расписания, при котором обслуживание каждого требования k завершается не позднее заданного директивного срока D_k. Появляется объективная необходимость в нарушении от­дельных директивных сроков, что сопряжено с определенными потерями. Эти потери, как правило, зависят от того, какие именно требования и на сколько задерживаются с обслуживанием. Иными словами, каждому требованию отнесена неубывающая кусочно-непрерывная функция штрафа _k(x)=0 при х  D_k и _k(x)>0 при х > D_k. Требуется определить расписание обслужива­ния п требований, при котором суммарный штраф наи­меньший.

В [1] предлагается алгоритм конструирования оптимальной относительно F_() последовательности обслуживания требований, когда _k(x)=max(x-D_k,0), :

1. Упорядочим множество N всех требований по не­убыванию значений D_k. Обозначим полученную последовательность ^D=(i₁, i₂,i₃ . . ., i_n). Если при этом все требования обслуживаются в срок, то ^D - оптимальная последовательность.

2. Упорядочим множество N всех требований по не­убыванию значений t_k. Обозначим полученную последо­вательность ^t=(j₁, j₂,j₃ . . .,j_n).Если при этом Di_k<Di_j. или 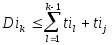, то ^t - оптимальная последовательность.

3. Из множества N выберем требование Ln с t_Ln = max (t_k). Если D_k<max(t_Ln,D_Ln) для всех kN, то в оптимальной последовательности это требование мож­но обслуживать последним .

4. Среди требований множества N_p выберем требова­ние L_n-р с D_Ln-р= mах D_k. Если t_Ln-р+ D_k>t_l для всех kN_p, то в оптимальной последовательности требования множества Np будут обслуживаться первыми в порядке неубывания значений D_k. В про­тивном случае обозначим N_p через М.

5. Разобьем множество М на два подмножества М₁ и М₂ по следующему принципу: если для jM существует iM такое, что интервал (₁=0, ₂=tk) является интервалом очередности типа i  j , to jM₂, остальные требования принадле­жат множеству М₁. Иными словами, множество M₁ со­стоит из конкурентноспособных претендентов на первооче­редное обслуживание в оптимальной последовательности среди всех требований множества М.

6. Выберем произвольное требование L₁M₁ и пред­положим, что в оптимальной последовательности это тре­бование обслуживается первым среди всех требований множества М. Уменьшим значение D_k для всех kM, kL₁ на величину t_L1 и перейдем к выполнению пп. 3—4, полагая N = М \ L₁. Таким образом, в результате при­нятия гипотезы, что первым в оптимальной последователь­ности обслуживается требование L₁, получаем множество М (L₁)M все еще неупорядоченных требований. Аналогичные рассуждения проводим относительно ос­тальных требований множества М₁.

7. Перейдем к последовательному рассмотрению ситуа­ций вида: требование L₁ обслуживается первым и М (L₁) — множество все еще неупорядоченных требований. Повто­ряем пп. 5, 6, полагая М =- М (L₁) и принимая в качестве D_k значения исходных директивных сроков, уменьшенных на величину t_L1. Затем перейдем к последовательному рассмотрению ситуаций вида: требования L₁, L₂, обслуживаются первыми в последовательности (L₁, L₂) и M(L₁, L₂) - множество все еще неупорядоченных требований и т.д.

В результате получаем конечное множество последовательностей, среди которых выбираем последовательность ^*, которой соответствует наименьшее значение F_(). Эта последовательность является искомой.