5. Выборочное исследование

Допустим, что проведено бесповторное выборочное наблюдение в северо-западных регионах РФ по величине числа умерших от болезней органов дыхания. Данные и расчеты представлены в таблице 5.1

Таблица 5.1

Выборочное наблюдение по величине числа умерших от болезней органов дыхания

Северо-западные регионы РФ	Величина числа умерших от болезней органов дыхания, чел.	X -	(X - 2
г.Санкт-Петербург	1955	1313,45	1725162,84
Ленинградская область	1045	403,45	162775,57
Вологодская область	751	109,45	11980,30
Архангельская область	625	-16,55	273,75
Псковская область	611	-30,55	933,02
Республика Коми	548	-93,55	8750,75
Новгородская область	472	-169,55	28745,66
Республика Карелия	375	-266,55	71046,48
Калининградская область	353	-288,55	83258,48
Мурманская область	303	-338,55	114613,02
Ненецкий авт.округ	19	-622,55	387562,84
Итого:	7057		2595102,73

Где рассчитано по формуле:

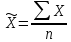= = 641,55 чел.

Найдем среднюю ошибку выборки по формуле:

где 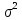- дисперсия признака в выборочной совокупности, которая рассчитывается по формуле:

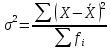= = 235918,43

136,40 чел

На основании средней ошибки вычисляется предельная ошибка выборки Δ=tμ, где t – коэффициент Стьюдента. При вероятности 0,993 t=3, поэтому предельная ошибка будет равна

Δ=3∙136,40 =409,19 (чел.)

Тогда получаем границы изменения генеральной средней:

– Δ ≤ + Δ;

641,55 – 409,19 ≤ 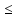641,55+409,19

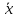
232,35 ≤ 1050,74.

Найдем, какое количество регионов необходимо обследовать для того, чтобы снизить предельную ошибку выборки на 50%. Новая ошибка будет равна Δ’ = 0,5Δ = 204,60 чел., а новая выборочная совокупность будет содержать количество регионов, которое для бесповторного отбора находится по формуле:

В данном случае:

Итак, среднее значение величины числа умерших от болезней органов дыхания по всей генеральной совокупности с вероятностью 0,993 лежит в интервале от 232,35 до 1050,74 чел. Чтобы снизить предельную ошибку выборки на 50%, необходимо увеличить объем выборочной совокупности до 32 регионов.

6. Индексы

В таблице 6.1 представлены данные о выпуске в РФ продукции трех видов сахаpа-песка, макаронных изделий и муки за 2008 г. (базисный период) и 2009 г. (отчетный период). p₀ и р₁ - цены за единицу продукции в базисном и отчетном периоде соответственно, а q₀ и q₁ – объем продукции в тех же периодах.

Таблица 6.1

Данные о выпуске продукции по видам и ценам за 2008 и 2009 г.

Вид продукции	2008 г.					2009 г.
	qo	p0	p0q0	p1q0	q1		p1	p1q1	p0q1
Сахар-песок	5873	25,07	147236,11	200269,3	5023		34,1	171284,3	125926,61
Макаронные изделия	1027	44,74	45947,98	43852,9	1048		42,7	44749,6	46887,52
Мука	10,3	21,63	222,789	191,58	10,2		18,6	189,72	220,626
Итого	6910,3	91,44	193406,88	244313,78	6081,2		95,4	216223,62	173034,76

Определим индивидуальные индексы объема, цены и стоимости по каждому из трех видов продукции и проверим их взаимосвязь.

По сахар-песку:

По макаронным изделиям:

По муке:

Определим общие индексы физического объема и цены по методам Ласпейреса и Пааше, а также общий индекс стоимости.:

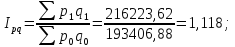
Результаты вычислений занесем в таблицу 6.2.

Таблица 6.2

Индексы физического объема, цены и стоимости

Индексы	Вид продукции				Общий
	Сахар-песок	Макаронные изделия	Мука
Цены	1,36	0,95	0,86	1,2323
Физического объема	0,86	1,02	0,99	0,8947
Стоимости	1,16	0,97	0,85	1,118

Итак, в 2009 г. объем товарооборота на исследуемом предприятии увеличился на 11,8%, что произошло в результате увеличения стоимости сахара-песка на 16%, тогда как стоимости макаронных изделий и муки упали на 3% и 15% соответственно.

За счет изменения физического объема товарооборот уменьшился на 10,53%, что произошло в результате увеличения физического объема на макаронные изделия на 2%, при этом объемы сахара-песка и муки упали на 14% и 1 % соответственно.

За счет изменения цен товарооборот увеличился на 23,23%, что произошло в результате увеличения цены сахара-песка на 36%, при одновременном уменьшении цен макаронных изделий и муки на 5% и 14 %.

Определим индексы переменного состава, постоянного состава и структурных сдвигов.

_.= = = 1,27

= = 1,25

₌= 1,02

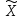
Итак, средняя цена производства увеличилась по сравнению с базисным годом на 27%. За счёт изменения цен на отдельные виды продукции средняя цена увеличилась на 25%, а за счет структурных сдвигов средняя цена увеличилась на 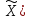2%.