Экзаменационный билет № 1

1. Детерминированные и случайные сигналы

Два вида моделей сигналов. При анализе физических данных используются два основных подхода к созданию математических моделей сигналов.

Первый подход оперирует с детерминированными сигналами, априорно известными или точно предсказуемыми. С математических позиций детерминированный сигнал - это сигнал, который с достаточной степенью точности можно описать явными математическими формулами или вычислительными алгоритмами.

Второй подход предполагает вероятностный (случайный) характер сигналов, которые можно описать только с использованием усредненных (статистических) характеристик. Случайность может быть обусловлена как собственной физической природой сигналов, так и определенным вероятностным характером регистрируемых сигналов как по времени их появления, так и по содержанию.

Между этими двумя видами сигналов нет резкой границы. Строго говоря, детерминированных процессов и отвечающих им детерминированных сигналов не существует. Даже сигналы, хорошо известные всегда осложнены случайными помехами, влиянием дестабилизирующих факторов и априорно неизвестными параметрами и строением внешней среды. С другой стороны, модель случайного поля часто аппроксимируется методом суперпозиции (сложения) сигналов известной формы.

1.4.1. Детерминированные сигналы

Обычно выделяют два класса детерминированных сигналов: периодические и непериодические.

К периодическим относят гармонические и полигармонические сигналы.

Гармонические сигналы (рис. 1.4.1), описываются следующими формулами:

или

где А, , , ,  - постоянные величины: А - амплитуда сигнала,  - циклическая частота в герцах,  - угловая частота в радианах,  и - начальные фазовые углы в радианах. Период одного колебания . При 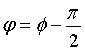синусные и косинусные функции описывают один и тот же сигнал. Частотный спектр сигнала представлен амплитудным и фазовым значением одной частоты.

Рис. 1.4.1. Гармонический сигнал и его АЧХ.

Полигармонические сигналы составляют наиболее широко распространенную группу периодических сигналов (рис. 1.4.2) и описываются выражениями:

или: , k = 1,2,3,..., где - период одного полного колебания сигнала. Число циклов колебаний за единицу независимой переменной t называют фундаментальной частотой 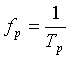. Полигармонические сигналы представляют собой сумму определенной постоянной составляющей и произвольного (в пределе - бесконечного) числа гармонических составляющих с частотами, кратными фундаментальной частоте f_p, и с произвольными значениями амплитуд A_n и фаз . Другими словами, частотный спектр полигармонических сигналов дискретен, поэтому получило широкое распространение математическое представление сигналов - в виде спектров (рядов Фурье).

Рис. 1.4.2. Полигармонический сигнал и его АЧХ.

К непериодическим сигналам относят почти периодические и апериодические или переходные сигналы.

Почти периодические сигналы близки по своей форме к полигармоническим (pис. 1.4.3). Они также представляют собой сумму двух и более гармонических сигналов, но не с кратными, а с произвольными частотами, отношения которых (хотя бы двух частот минимум) не относятся к рациональным числам, вследствие чего фундаментальный период суммарных колебаний бесконечно велик. Как правило, почти периодические сигналы порождаются физическими процессами, не связанными между собой.

Частотный спектр почти периодических сигналов также дискретен.

Рис. 1.4.3. Почти периодический сигнал и его АЧХ.

Апериодические сигналы составляют основную группу непериодических сигналов и задаются произвольными функциями времени (рис. 1.4.4). Например:

Частотный спектр апериодических сигналов непрерывен и для их представления в частотной области используется интегральное преобразование Фурье.

Рис. 1.4.4. Апериодический сигнал и модуль его спектра.

К апериодическим сигналам относятся также и импульсные сигналы. Импульсы представляют собой сигналы достаточно простой формы (рис. 1.4.5), существующие в пределах конечных временных интервалов.

Рис. 1.4.5. Импульсный сигнал и модуль его спектра.