3. Идеальный газ

3.1. Понятие идеального газа

Как отмечалось в разделе 2, состояние ТД системы с фиксированным числом частиц определяется тремя её параметрам состояния: р, V и Т, причём эти параметры не являются независимыми. а связаны некоторым соотношением:

f(p,V,Т)=0, (1)

которое называется уравнением состояния системы. Его конкретный вид зависит от свойств системы.

Простейшей ТД системой является идеальный газ.

Определение. Газ, взаимодействия между молекулами которого сводятся к упругим столкновениям, называется идеальным. Внутренняя энергия идеального газа − это только кинетическая энергия хаотического движения его молекул.

Всякий реальный газ при достаточном разрежении близок по свойствам к идеальному. При комнатной температуре и атмосферном давлении такие газы, как кислород, азот, а особенно водород и гелий очень близки по свойствам к идеальному. Но такие газы, как Н₂О и СО₂ при тех же условиях уже заметно отличаются от идеального.

3.2. Закон Авогадро

В 1811 году Авогадро экспериментально установил следующий факт, сформулированный в виде закона: при одинаковых давлении р и температуре Т моль любого идеального газа занимает одинаковый объём. В частности. при нормальных условиях, т.е. при р=1 атм=1,013·10⁵ Па и Т=273,15 К=0°С, один моль идеального газа (содержащий N_А=6·10²³ молекул) занимает объём (молярный объём)

V_M=22,4 литра=2,24·10⁻² м³/моль.

3.3. Уравнение состояния идеального газа

На основе опытов Бойля и Гей-Люссака установлено, что для одного моля идеального газа общее уравнение состояния (1) имеет следующий конкретный вид:

=const=R, (2)

где р – давление газа, V_M – его молярный объём, Т – температура, R – некоторая константа, называемая газовой постоянной. Её значение можно найти из закона Авогадро, подставив в (2) р=1,01·10⁵ Па, V_M=2,24·10⁻² м³/моль, Т=273 К. Это даёт

R=8,31 Дж/(моль·К).

А так как объём ν молей газа V=νV_M, то уравнение (2) для произвольного количества идеального газа примет вид

pV=νRT, (3)

или

pV=, (4)

где m – масса газа, М (кг/моль) – его молярная масса, ν=m/M – число молей.

Теперь можно дать следующее функциональное определение идеального газа: всякий газ, состояние которого описывается уравнением (3), называется идеальным.

Уравнение состояния идеального газа в форме (3) или (4) называется уравнением Клапейрона-Менделеева. Его можно представить в следующей эквивалентной форме: так как ν=N/N_A, то из (3) получаем

,

где =1,38·10⁻²³ Дж/К – постоянная Больцмана, п=N/V – концентрация молекул газа.

3.4. Внутренняя энергия идеального газа

Внутренняя энергия идеального газа – это сумма кинетических энергий всех его молекул:

U=∑W_к=N,

где N – число молекул в газе. А так как , где i – число степеней свободы молекулы, то

.

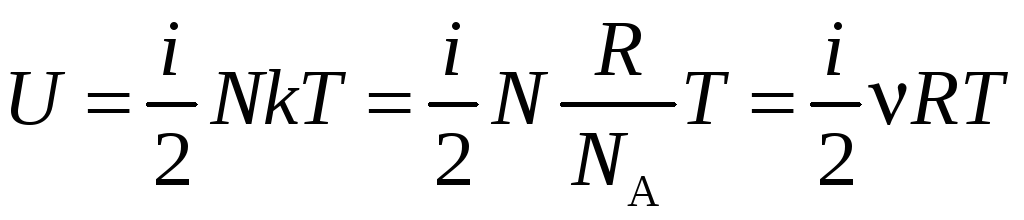Таким образом, внутренняя энергия идеального газа зависит только от его температуры и не зависит от давления: U=U(T)≠f(p).