Логнормальное распределение непрерывной случайной величины.

Одним из самых близких к нормальному распределению является логнормальное распределение, имеющее слабую левую асимметрию и относящееся ко второму типу распределений. Очевидно, что многие геохимические компоненты не подчиняются нормальному распределению, например концентрация селена в растительном материале, концентрация йода в грунтовых водах подчиняются асимметричным распределениям. Кривая логнормального распределения отражена на рисунке.

Существуют две физические причины асимметричности. Первая причина кроется в пороге чувствительности приборов, определяющих концентрацию редких химических элементов (селен, радий и др.). Левая асимметричность возникает, из-за того, что много данных концентрируется около порога чувствительности, и если бы этого порога не было, то распределение приняло бы нормальный симметричный вид.

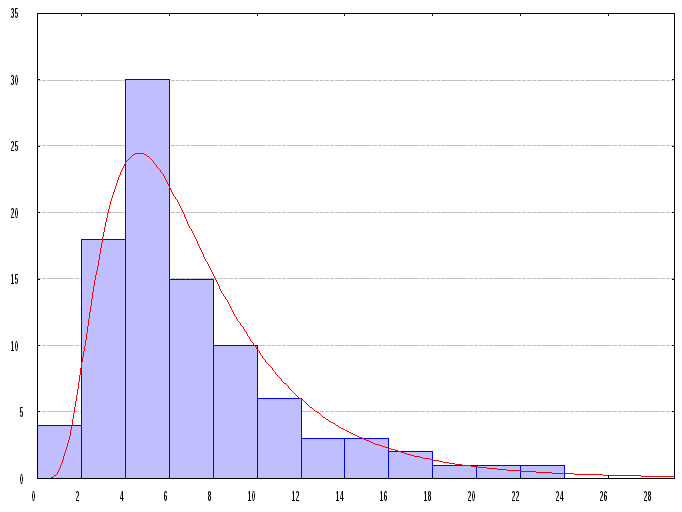
Рис. Кривая логнормального распределения.

Вторая причина кроется в детерминированности изменений природных объектов, тем более мощные геохимические и тектонические процессы, которые протекали при формировании залежей полезных ископаемых, тем более кривая распределения характеристик этих залежей будет асимметричной. Асимметричность, например, возникает, если толкать спортсмена-стрелка в тире в момент выстрела, в этом случае пули на мишени будут располагаться преимущественно с одной стороны мишени. Если результаты наблюдений, распределение которых представлено на рисунке, прологарифмировать (то есть вместо переменной x_i использовать переменную y = log x_i), то распределение прологарифмированной переменной примет нормальный вид. Все перечисленные ранее параметры и статистики также характерны и пригодны и для логнормального распределения. На практике они рассчитываются по тем же формулам, только предварительно все значения выборки логарифмируются, однако основные статистики можно посчитать, используя и не преобразованные данные, в этом случае среднеарифметическому значению будет соответствовать геометрическое среднее, а значению дисперсии будет соответствовать геометрическая дисперсия. Преобразования типа y = log x_i широко применяются в геологии, однако известно (У.Крамбейн, Ф.Грейбилл) и так называемое фи - преобразование - φ = - log x_i. Это преобразование используется, например, при изучении распределений размеров частиц осадочных пород.

Лекция 8.

Гамма-распределение непрерывной случайной величины и его разновидность - распределение Пуассона непрерывной случайной величины.

Гамма - распределение относится по классификации Пирсона к третьему типу кривых, в этот тип входит обширная группа асимметричных распределений (в том числе и бета – распределение). Данные, которые подчиняются этим распределениям, никакими преобразованиями не могут быть преобразованы таким образом, чтобы после они имели нормальное распределение. Однако одна из разновидностей гамма - распределения имеет для нас значение, так как существуют способы преобразования данных, после которых они могут подчиняться логнормальному и нормальному распределению. Плотность вероятности гамма - распределения описывается следующей формулой

G (x;Γ;β) = x^r-1*e^-χ/β/ Γ(г) β^r x≥0, r >0, β>0.

Дополнительными параметрами гамма - распределения являются величины r и β, первый является параметром положения, а второй параметром масштаба.

Рис Примеры кривых плотности вероятности, соответствующие различным значениям r, при β = 1.

Выбор гамма распределения в качестве модели распределения изучаемой совокупности определяется наличием у изучаемой кривой распределения так называемого хвоста, являющегося следствием асимметричности распределения и препятствующим различным математическим преобразованиям привести экспериментальные данные к нормальному или логнормальному распределению. Так же как и для нормального распределения плотности вероятности распределения, выраженные через площади под кривой распределения, давно рассчитаны и опубликованы в таблицах. Вычислить и оценить параметры - r и β можно по таблицам Сиддикуи и Вейса и через них рассчитать μ и σ² (то есть истинное среднее совокупности и ее дисперсию) по формулам

μ = β* r;

σ²= β²* r.

Как видно из этих формул, для гамма - распределений отмечается сильная зависимость между средним и дисперсией, тогда как в случае нормального распределения такой зависимости нет.

Основные компоненты полиметаллических месторождений, месторождений цветных металлов и золота могут подчиняться разновидностям гамма – распределения. Частным случаем, гамма распределений является распределение Пуассона, если его использовать для анализа непрерывных случайных величин. Особенно это распределение характерно для месторождений золота, так как именно в большей части на этих месторождениях часты находки самородков золота (редкие события) или можно перефразировать - встречаются пробы с аномальным высоким содержанием золота (ураганные пробы), во много раз превышающим наиболее распространенные содержания металла по конкретному месторождению (эффект самородков). Несмотря на то, что гамма - распределения, в том числе и распределение Пуассона хорошо изучены на практике, специалисты стараются не использовать эту модель для оценки истинных параметров изучаемой совокупности из-за ряда причин, в том числе и из-за сильной зависимости между средним и дисперсией. Для решения этой задачи общепринят иной подход, при котором эффект самородков стараются нейтрализовать и затем после возможных преобразований данных предположить нормальную модель их распределения.

Учет ураганных проб.

Сама проблема ураганных проб предполагает две стадии ее решения, в первую стадию, нужно выявить ураганные пробы, а во вторую стадию их нейтрализовать. Существует много способов регистрации ураганных проб, и они подробно описаны в специализированной литературе [ 5 ]. Однако в последнее время среди специалистов наибольшую популярность получили “квантильный” способ обнаружения ураганных значений металлов в пробах и способ обнаружения ураганных проб по излому на кумулятивной кривой распределения, описанные в книге Ю.Е. Капутина “Горные компьютерные технологии и геостатистика”. Если придерживаться терминологии предложенной в этих лекциях, то первый способ можно назвать децильным способом, так как массив проб сначала сортируется по величине содержания металла от минимального до максимального, затем строится частотная таблица и гистограмма. А после таблица разделяется на заданное количество квантилей, обычно на 10 частей (то есть массив разделяется на децили). В результате формируется таблица, пример которой приведен ниже.

Класс	Число записей	Среднее значение	Минимум	Максимум	Доля металла с данным содержанием от всей выборки	Доля металла с данным содержанием от всей выборки (%)
0-10	1110	0.004	0.000	0.010	4.805	0.07%
10-20	1110	0.010	0.010	0.018	11.522	0.16%
20-30	1110	0.021	0.018	0.030	23.816	0.34%
30-40	1110	0.035	0.030	0.049	38.823	0.55%
40-50	1110	0.052	0.049	0.060	57.571	0.82%
50-60	1110	0.080	0.060	0.100	88.946	1.27%
60-70	1110	0.128	0.100	0.160	141.922	2.02%
70-80	1110	0.219	0.160	0.290	243.590	3.47%
80-90	1110	0.426	0.290	0.640	472.534	6.73%
90-100	1106	5.370	0.640	305.310	5938.771	84.57%
ВСЕГО	11096	0.633	0.000	305.310	7022.301	100.00%
90-91	111	0.677	0.640	0.720	75.161	1.27%
91-92	111	0.777	0.720	0.840	86.204	1.45%
92-93	111	0.896	0.840	0.950	99.474	1.67%
93-94	111	1.029	0.950	1.120	114.198	1.92%
94-95	111	1.238	1.120	1.390	137.390	2.31%
95-96	111	1.587	1.390	1.790	176.153	2.97%
96-97	111	2.046	1.790	2.350	227.100	3.82%
97-98	111	2.899	2.360	3.690	321.840	5.42%
98-99	111	5.497	3.700	8.660	610.180	10.27%
99-100	107	38.234	8.670	305.310	4091.070	68.89%
ВСЕГО	1106	5.370	0.640	305.310	5938.770	100.00%

Если последний класс (90-100%) содержит долю металла, большую чем 40% от общего количества, то считается, что в массиве данных существуют ураганные пробы. Далее рассчитывается аналогичная таблица для последнего класса. Границей для ураганных проб считается минимальное содержание первого класса, содержащего долю металла более 10%. В данном примере – это 3.7 г/т. Считается, что подобный анализ нужно проводить для каждого типа руд, и для каждого участка месторождения. На практике отмечается много случаев, когда границы ураганных проб на одном и том же месторождении резко отличались друг от друга на разных его участках.

Второй способ состоит в том, что строится кумулятивное распределение массива данных, но отображается оно в виде огивы и исследуется конечная часть хвоста распределения. На графике отмечается место перегиба кумулятивной кривой, которое и является границей, после которой фиксируются ураганные пробы.

Рис . Определение границы, после которой фиксируются ураганные пробы по месту излома огивы (вместо накопленных частот по оси абсцисс фиксируются соответствующие номера проб).

Существуют еще более простые методы выявления ураганных проб, можно например, просто определить ураганные пробы в хвосте массива распределения, после достижения 95% или 99% накопленных частот или использовать соотношение между модой, медианой и среднеарифметическим значением которое, характерно для умеренно асимметричных кривых -

M_o– χ=3(M_e – χ).

Есть несколько подходов и к нейтрализации ураганных проб.

1. Можно исключить аномальные значения из выборки (например, просто отрезать хвост распределения после достижения 95%-99% накопленных частот).

2. Можно вместо аномальных значений указать пороговые значения, при которых выборочные данные будут иметь нормальное или логнормальное распределение.

3. Можно присвоить аномальным значениям среднеарифметические значения выборки.

Подразумевается, что в первом и третьем случае, после процедур данные будут иметь нормальное или логнормальное распределение. Однако вопрос и о способах выявления и о необходимости нейтрализации ураганных проб остается открытым, так как в любом случае, мы можем допустить еще большую ошибку при оценке истинных параметров, как всей изучаемой совокупности, так и ее частей. Так, например, нейтрализация ураганных проб в выборке, при разведке месторождений золота может уменьшить оценку запасов месторождения, но главное значительно ухудшить экономическую оценку месторождения, из-за высокой цены на этот металл. Тем не менее, большинство специалистов соглашаются, что лучшим выбором для оценки параметров будет выбор нормальной модели распределения выборочных данных. То есть наши оценки параметров будут более точными, чем ближе к нашему экспериментальному распределению будет подходить нормальная модель распределения.

Кроме логарифмирования данных и нейтрализации ураганных проб можно предложить и другие полезные преобразования данных, после которых наши данные могут быть ближе к нормальному распределению. Одно из таких преобразований это преобразование типа - y_i=√x_i и оно в ряде случаев может привести к сокращению пуассоновского хвоста, если наблюдаемые значения близки к 0, то используют преобразование типа - y_i=√x_i +1/2. Можно использовать также и степенные преобразования, в этом случае больше будут увеличиваться большие значения, чем малые, ко всему прочему это преобразование позволяет лучше читать каротажные диаграммы.