Нормальное распределение непрерывной случайной величины.

Измерения, проводимые на больших выборках, взятых из природных совокупностей, позволяют охарактеризовать самое известное распределение из всех распределений непрерывной случайной величины. Обычно большая часть значений в этом распределении группируется около некоторого центрального значения, при удалении от которого частоты резко убывают. График частот имеет один максимум, и само распределение называется нормальным распределением случайной непрерывной величины.

Рис. График нормального распределения случайной величины.

Часто делаются допущения, что если какие либо непрерывные случайные величины распределены нормально, то для их анализа можно использовать большинство статистических критериев, о которых пойдет речь ниже, то есть многие разработанные статистические критерии основаны на этом допущении. Общая площадь, заключенная между графиком нормального распределения и горизонтальной осью равна 1 (или 100%). Первоначально нормальный закон распределения случайной величины вывел Гаусс в 18 веке. Нормальный закон распределения случайной величины называют еще Гауссовой функцией ошибок, которую он вывел на основе анализа случайных ошибок при наблюдениях природных объектов. Однако в дальнейшем оказалось, что очень много результатов измерений описываются Гауссовой кривой распределения.

Аналитическое выражение кривой распределения есть дифференциальная функция распределения.

φ(x) = dF(x)/dx

То есть вероятность того, что случайная величина x примет значение в пределах A< x >B, численно равна площади под кривой распределения, заключенной между ординатами A и B. Поэтому дифференциальную функцию распределения называют плотностью вероятности или плотностью распределения.

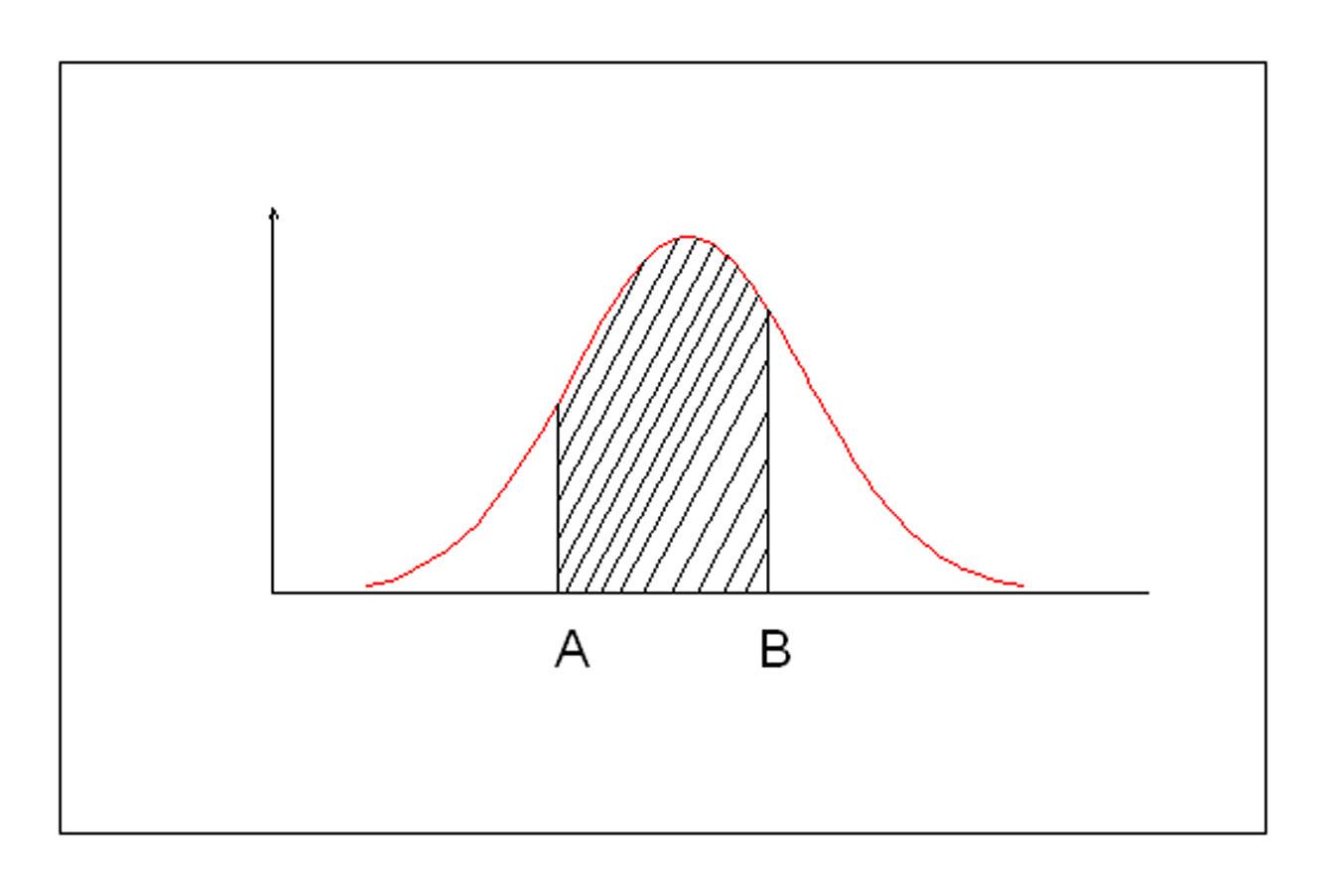
Рис. Плотность вероятности нормального распределения случайной величины.

Нормальное распределение случайной величины имеет ряд характерных свойств.

1. Частоты относительно середины графика располагаются примерно симметрично.

2. Чем меньше по абсолютной величине ошибки, тем чаще они встречаются.

3. Кривая распределения частот похожа на колокол – отмечается резкое падение частот по мере удаления от середины графика и далее постепенное выполаживание кривой.

Нормальное распределение обычно возникает, когда производятся повторные измерения некоторой величины. При каждом индивидуальном измерении возникает множество причин, воздействующих на объект измерения, часто в противоположных направлениях, часть этих воздействий взаимно уничтожается, часть нет, и это все и отображается на колоколообразной кривой нормального распределения.

Параметры и статистики.

Все непрерывные распределения совокупностей имеют ряд характеристик, таких как среднее положение распределения, положения распределения, делящие его на равные части, мера разброса относительно среднего положения и характеристики симметрии и формы изучаемых кривых распределений. Наиболее удобно проанализировать эти характеристики на примере как раз нормального распределения непрерывной случайной величины. Будем называть эти характеристики параметрами, если они характеризуют совокупность и статистиками, если они рассчитаны из выборочных данных. Статистики обычно являются оценками параметров изучаемых совокупностей, а сами параметры являются истинными характеристиками изучаемых объектов. Важной особенностью нормального распределения является то, что по плотности распределения или по размеру площади под кривой распределения, заключенной между какими-либо ординатами мы можем оценить величину ошибки при проведении наших измерений.

Среднее положение распределения.

Наиболее очевидная характеристика – это среднее положение распределения. Существует несколько видов среднего положения распределения, но только некоторые из них используются на практике.

Рис. Соотношение моды, медианы и среднеарифметического на графике непрерывного распределения случайной величины.

Первая характеристика – это мода. В распределении, приведенном на рисунке, мода соответствует средней точке на оси абсцисс, находящейся под наивысшей точкой кривой частот и в принципе соответствует обиходному пониманию этого слова - мода. Модно то, что наибольшее количество людей на себя надевает и носит.

Моду можно рассчитать по следующей формуле:

M_o = x_o +i*{(f_mo-f_mo-1)/[(f_mo-f_mo-1)+(f_mo-f_mo+1)]}

Где x_o – нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту), i – величина модального интервала, f_mo – частота модального интервала, f_mo-1 , f_mo+1 - соответственно частота интервала, предшествующего модальному и следующему за модальным.

Вторая характеристика – это медиана. Медиана соответствует средней точке на оси абсцисс, так перпендикуляр, проведенный через эту точку, делит площадь под кривой пополам, то есть половина площади от этой точки находиться справа, а половина находится слева. Главное свойство медианы заключается в том, что сумма абсолютных отклонений признака от медианы меньше, чем от любой другой величины. Медиану можно рассчитать по следующей формуле:

M_e = x_e +i* {[(1/2∑fi)- Sf_me-1]/Sf_me}

где x_e – нижняя граница медианного интервала (медианным интервалом называется первый интервал, накопленная частота которого превышает половину общей суммы частот), i – величина медианного интервала, Sf_me-1 – накопленная частота интервала, предшествующего медианному, Sf_me – частота медианного интервала. (1/2∑fi – равна 50%).

И третья самая важная характеристика это точка на оси абсцисс, соответствующая среднеарифметическому значению, которое рассчитывается как сумма всех результатов наблюдений, деленная на их число.

χ=∑x_i/n

Основной характеристикой центра распределения является средняя арифметическая, все отклонения от нее (положительные и отрицательные) равны 0, для медианы характерно, что сумма отклонений от нее по модулю является минимальной, а мода представляет значение признака, которое наиболее часто встречается. Соотношение моды, медианы и среднеарифметической позволяет оценить асимметрию распределения. В симметричных распределениях все три характеристики совпадают, чем больше расхождение между модой и среднеарифметической, тем больше асимметрия распределения. Для умеренно асимметричных распределений разность между модой и среднеарифметической в 3 раза превышает разность между медианой и среднеарифметической.

M_o– χ=3(M_e – χ).

Моду и медиану легко определить графически. Мода определяется по гистограмме распределения и соответствует самой высокой точке кривой или середине самого высокого прямоугольника гистограммы (середине модального интервала). Медиана определяется легко по кумулятивной кривой гистограммы, на ординате находится точка, соответствующая 50% накопленных частот из которой проводится до пересечения с кривой графика прямая, параллельная оси абсцисс, затем из точки пересечения опускается до оси абсцисс перпендикуляр, который и указывает на значение медианы.

Многие символы традиционно используются для обозначения кривых распределения, обычно для теоретических распределений или распределений совокупностей традиционно используются греческие буквы, а для обозначения характеристик выборок используются латинские буквы. Так среднее выборки обозначают как χ, а теоретическое среднее или среднее всей совокупности обозначают как μ. Статистика, которую мы вычисляем по выборке, используется как оценка истинного параметра совокупности. Использование в качестве обозначения характеристик греческих и латинских букв подчеркивает разницу между параметрами и соответствующими им статистиками. Среднеарифметическое значение, вычисленное по выборке, имеет два очень важных свойства, которые делают его более полезным для оценки истинного среднего или центрального положения распределения совокупности, чем любая из оставшихся характеристик (медиана или мода). Во-первых, среднеарифметическое выборки, в которой все пункты наблюдения, в которых проводились измерения, или отбирались пробы для последующих исследований, выбирались случайно, чаще всего является несмещенной оценкой истинного среднего значения совокупности. Во-вторых, для нормального распределения (как симметричного распределения) среднеарифметическое значение выборки характеризуется тенденцией лучшего приближения к истинному среднему или к среднему значению совокупности, чем медиана, посчитанная по той же выборке. Однако медиана нередко является лучшей оценкой среднего совокупности, когда мы имеем дело с асимметричными распределениями, когда результаты измерений не подчиняются нормальному распределению. Медиана позволяет в этом случае дать более объективную оценку среднего положения для большей части совокупности (до 99%), но не для 100 % совокупности.

Среднеарифметическое значение совокупности μ называют математическим ожиданием. Математическое ожидание определяется как сумма произведений всех возможных значений случайной величины на их вероятности:

μ= ∑x_i*p_i (p_i – вероятности появления значений случайной величины).

Эту формулу легко понять, так как среднеарифметическое значение рассчитывается как:

χ= (x₁*m₁ + x₂*m₂ …….x_n*m_n)/n = ∑x_i*(m/n)

где x_i - это значения переменной, n – это общее количество данных, m – это количество этих значений, а так как частота (m/n) появления события при увеличении количества опытов стремится к вероятности то и математическое ожидание совокупности можно рассчитать по формуле:

μ= ∑x_i*p_i .

В зависимости от характера имеющихся данных среднеарифметическое значение выборочных данных может быть рассчитано по разным формулам и в зависимости от этого она имеет разные названия. Широко используются четыре разновидности среднеарифметического значения.

1. Среднеарифметическое простое, не взвешенное значение, рассчитывается по приведенной уже формуле:

χ=∑x_i/n.

Можно легко рассчитать среднеарифметическое значение данных приведенных в таблице:

Содержание компонента в пробе (xi)	Количество проб (mi)	xi * mi
205	1	205
255	1	255
195	3	585
220	2	440
235	1	235
	Всего - 8	Всего - 1720

χ = 1720/8 = 215.

2. Среднеарифметическое значение - взвешенное, рассчитывается по формуле:

χ=(x₁*L₁+x₂*L₂+x₃*L₃+…..x_i*L_i)/(L₁+L₂+L₃…+ L_n) = ∑x_i*L_i/∑L_i.

Среднеарифметическое взвешенное значение возникает в геологической практике, когда берутся пробы, в которых производят измерения компонентов, разной длины. В этом случае подсчет среднего значения без взвешивания на длину пробы, приведет к ошибочному результату, так как не будет сохраняться пропорциональность, поэтому используют для расчета формулу взвешенного значения. Можно рассчитать средневзвешенное значение компонента из данных, приведенных в таблице по формуле.

L – длина пробы	Xi – значение компонента в %
2	0.2
2.5	0.5
1.8	0.3

χ= (2*0.2+2.5*0.5+1.8*0.3)/(2+2.5+1.8)=0.347

Однако для учета пропорциональности используется и другой подход, часто средние значения и другие статистики рассчитывают после приведения длин проб к одной длине и пересчета содержаний компонентов на эту длину. Этот способ получил название – композитирование (compositing) проб, а такие пробы называют композитными пробами, в этом случае можно говорить о средневзвешенных значениях проб с учетом предварительного композитирования или о средневзвешенном композитном значении изучаемого компонента. В этом случае, если мы хотим композитировать на среднюю длину пробы в 2 метра, то нужно будет пересчитать содержания компонента, как в примере, показанном в ниже располагающейся таблице.

2	0.2
2	0.5
2	(0.5*0.5+1.5*0.3)/2 = 0.35

3. Средняя гармоническая взвешенная величина.

4. Средняя геометрическая величина.

Средняя геометрическая величина рассчитывается по формуле:

χ_G = ⁿx_1*x_2*x₃....x_n = ⁿ Пx_i.

И в случае если рассчитывается средняя геометрическая взвешенная величина, то ее рассчитывают по следующей формуле:

χ_G = ^∑mx₁^m1_*x₂^m2_*x₃^m3....x_n^mn = ^∑m П(x_i)^mi,

где m_i – вес i-го варианта.

Практическое значение средних геометрических величин станет ясным при рассмотрении асимметричных распределений.

Положения распределения, делящие его на равные части.

В непрерывных распределениях случайной величины, особенно если результаты наших измерений подчиняются нормальному распределению, можно найти значения компонента, по которым распределение делится на произвольное количество равных частей, на четыре равные части, на десять равных частей или сто равных частей, такие величины называют квантили, квартили, децили и перцентили.

Квартили представляют собой значения компонента, которые делят площадь под кривой распределения на четыре равных части. Нижний и верхний квартили отсекают по 25% соответственно снизу и сверху распределения, а средним квартилем является медиана. Для расчета нижнего и верхнего квартиля используются следующие формулы.

Q₁=x_q1 + i*[(1/4∑f – Sf_q1-1)/Sf_q1]

Q₃= x_q3 + i*[(3/4∑f – Sf_q3-1)/Sf_q3]

где Q₁, Q₃ – нижний и верхний квартиль, x_{q1 ,} x_q3 - соответственно нижняя граница интервалов, содержащих нижний и верхний квартиль (эти интервалы определяются по накопленным частотам, первый по накопленной частоте, превышающей 25%, второй по накопленной частоте, превышающей 75%), i - величина интервала, Sf - частоты соответствующих интервалов или частей распределения.

Кроме квартилей могут рассчитываться - децили, которые представляют собой значения компонента, делящие распределение на 10 равных частей. Они вычисляются по той же схеме, что квартили:

D₁=x_d1+i*[(1/10∑f – Sf_d1-1)/Sf_d1]

D₂=x_d2+i*[(2/10∑f – Sf_d2-1)/Sf_d2]

и так далее.

Перцентили используются при необходимости очень подробного изучения структуры распределения и рассчитываются по аналогичным формулам, что и децили.

Лекция 6.

Мера разброса относительно среднего положения распределения.

Одна из самых важных характеристик распределения – это мера разброса отдельных значений относительно среднего. Известны восемь различных мер этой характеристики, четыре из них широко используются в геологических прикладных науках.

1. Первая мера разброса значений относительно среднего – это размах распределения R:

R = max – min.

2. Вторая мера это дисперсия. Дисперсия – это среднее значение квадратов отклонений всех возможных значений случайной величины от истинного среднего совокупности μ:

σ² = 1/n*∑(x_i – μ)²

Этой формулой рассчитывают истинную дисперсию совокупности, обозначаемую символом σ². Выборочная дисперсия обозначается символом - S². Если пункты наблюдения, в которых отбирались пробы для измерения полезного компонента, были распределены равномерно и случайным образом на исследуемой территории и пробы отбирались из совокупности с нормальным распределением, то выборочная дисперсия S² является лучшей оценкой истинной дисперсии совокупности - σ². Однако для расчета выборочной дисперсии используется несколько видоизмененная формула:

S²=1/n-1 * ∑ (x_i-χ)² , или

S²=1/n-1 *[∑ x_i² –1/n(∑ χ)²], или

S²=1/n*(n-1) *[n∑ x_i² – (∑ χ)²].

По этой формуле дисперсия определяется как среднее значение от суммы квадратов отклонений от выборочного среднего и появляется новая величина – (n-1), требующая пояснений. Так как при изучении залежей полезных ископаемых и других природных объектов, мы никогда не знаем истинного среднего совокупности μ, а для расчета дисперсии используем оценку истинного среднего - χ, то в этом случае мы занижаем оценку истинной дисперсии. Это связано с тем, что при суммировании квадратов отклонений от выборочного среднего мы находим минимальное значение из всех возможных. При симметричном распределении отклонения от среднего в одну и в другую сторону равны и если, не возводить отклонения в квадрат, то сумма их будет равна нулю. Но если истинное среднее не совпадает с оценочным средним, то симметрия нарушается и рассчитывается большая величина дисперсии. Что бы улучшить оценку дисперсии вместо n в формулу вводится n-1. Введение в формулы вместо количества данных в выборке - n, - n-1, n-2 и так далее – это общее правило в статистике, которое называется учетом степеней свободы, а количество данных с поправкой (n-1, n-2 и так далее) – называется числом степеней свободы. Это правило применяется, когда при расчетах в формулах вместо истинных значений (параметров), используются оценочные значения (статистики), то есть, если в какой-либо формуле, например, используются 2 оценки параметров, то от количества данных отнимают 2 и так далее.

3. Третья мера – стандартное отклонение. Для того чтобы получить параметр, который характеризует разброс данных относительно среднего значения и обладает той же размерностью, что и исходные данные можно воспользоваться третьей мерой разброса – стандартным отклонением или еще эту меру называют средне квадратичным отклонением. Она рассчитывается как квадратный корень из дисперсии и обозначается символом – σ, а стандартное отклонение выборки обозначается символом - S. Небольшое значение стандартного отклонения показывает, что результаты опробования залежи полезного ископаемого группируются около центрального значения и наоборот большое значение стандартного отклонения показывает, что результаты опробования рассеяны относительно среднего значения. Стандартное отклонение иллюстрирует изменчивость характеристик залежи, чем больше стандартное отклонение, тем меньше у нас шансов правильно оценить такие характеристики, как запасы полезных компонентов залежи. Очень полезное свойство нормального распределения заключается в том, что площадь под кривой распределения в пределах любого интервала может быть точно вычислена. Так более 2/3 результатов (68.27%) попадает в интервал равный двум стандартным отклонениям (плюс и минус стандартное отклонение от истинного среднего μ). Примерно 95% всех значений заключается в интервале от -2 до +2 стандартных отклонений от среднего μ и более 99% значений содержится в интервале от -3 до +3 стандартных отклонений от среднего μ. Это отражено на рисунке, расположенном ниже.

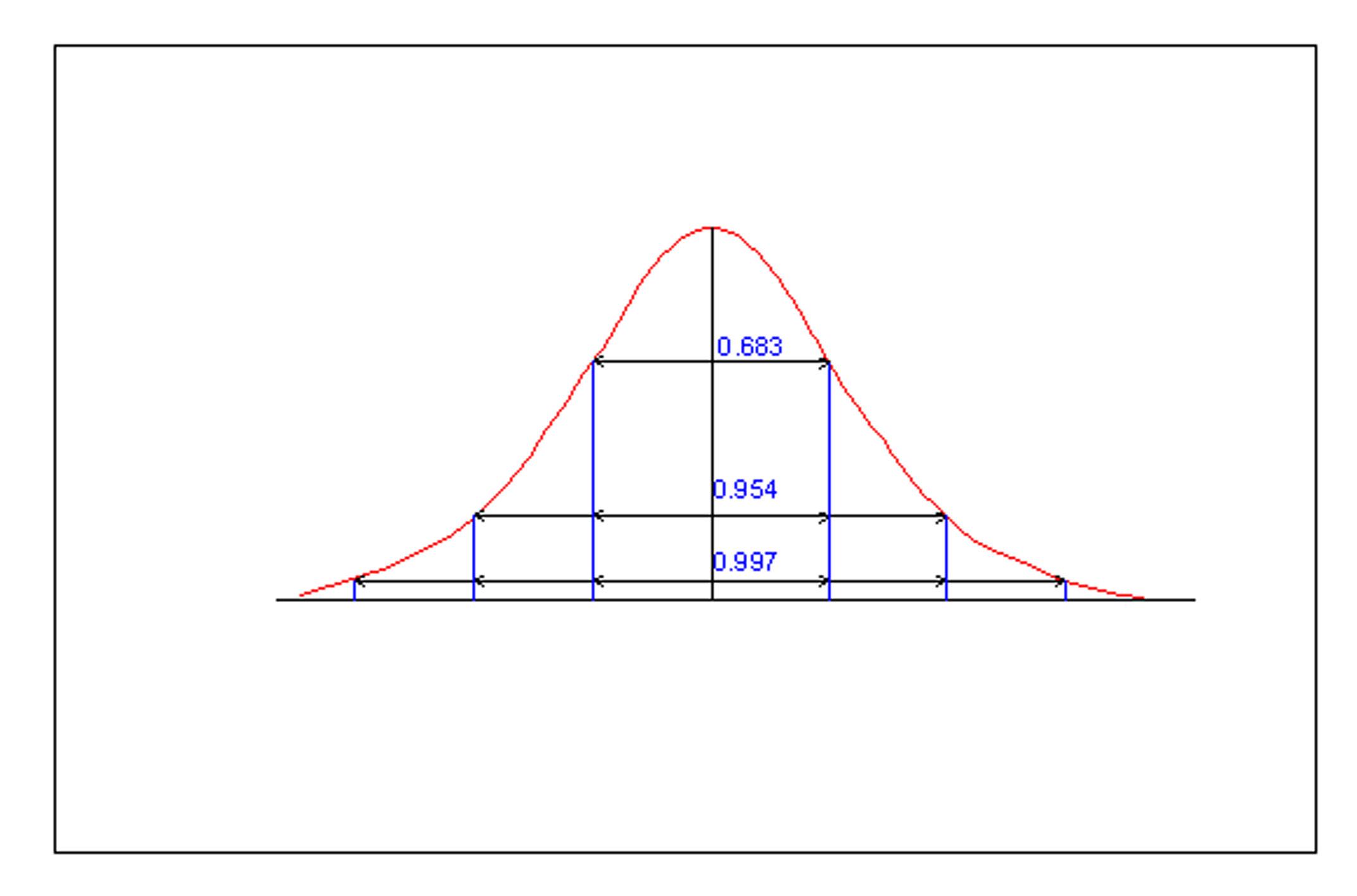
Рис. Площади стандартного нормального распределения, заключенные в пределах интервалов, кратных стандартному отклонению.

Это свойство нормального распределения называют правилом - 3-х σ. Из этого правила следует очень важный вывод о том, что если новое измерение какого либо свойства превышает величину, равную 3-м σ, то можно это значение отнести к аномальным значениям. То есть, если говорить формальным языком, то этот результат измерения с очень маленькой вероятностью относится к изучаемой совокупности. Это позволяет эффективно выявлять возможные аномальные значения среди постоянно изменяющихся показаний приборов.

4. Четвертая мера – это коэффициент вариации. Его часто используют при разведке и оценке месторождений полезных ископаемых. Коэффициент вариации определяется как отношение стандартного отклонения на выборочное среднее и умноженное на 100%. Важным свойством коэффициента вариации является его безразмерность, поэтому он так широко и используется в различных методических руководствах, регламентирующих проведение геологоразведочных работ:

V_S = (S/χ)*100.

Остальные меры разброса значений относительно среднего, такие как коэффициент осцилляции, среднее линейное отклонение, относительное линейное отклонение и геометрическая дисперсия используются реже.

5. Пятая мера - коэффициент осцилляции, он рассчитывается по формуле:

V_R= (R/χ)*100, где R = max – min.

6. Шестая мера – среднее линейное отклонение, рассчитывается по формуле:

d = (∑|x_i - χ|)/n.

7. Седьмая мера – это относительное линейное отклонение, рассчитывается по формуле:

V_d = (d/χ)*100.

8. Восьмая мера – геометрическая дисперсия. Она рассчитывается по следующей формуле:

S²_G = ^n-1√П2(x_i/χ_G).

Практическое значение геометрической дисперсии станет ясным при рассмотрении асимметричных распределений.

Характеристики асимметрии и формы кривой распределения.

Для характеристики асимметрии и формы кривой распределения случайной величины служат коэффициент асимметрии и эксцесс.

Коэффициент асимметрии при нормальном распределении равен 0. Он рассчитывается по следующим формулам:

A = L₃⁰/S³,

L₃⁰ = (1/n-1)*[∑(x_i-χ)³].

Для обозначения L₃⁰ была использована та же формула, что и для расчета дисперсии, только отклонение от выборочного среднего возводится не в квадрат, а в третью степень. В этом случае, если наше распределение не будет симметричным, то и коэффициент асимметрии A не будет равен 0, то есть мы будем иметь или положительную или отрицательную асимметрию, как показано на рисунке.

Рис . Асимметричные распределения.

Если мы хотим оценить форму кривой распределения, насколько наша вершина кривой распределения острая или сглаженная, то пользуются понятием эксцесса, который рассчитывают по формуле:

Э = L₄⁰/S⁴ - 3,

L₄⁰ = (1/n-1)*[∑(x_i-χ)⁴].

Эксцесс нормального распределения равен 0, кривая с более острой вершиной будет иметь положительный эксцесс, а более пологая кривая будет иметь отрицательный эксцесс, как отражено на рисунке. Положительный эксцесс свидетельствует о ненормальном однообразии изучаемой совокупности, а отрицательный эксцесс свидетельствует напротив как раз о ненормальном разнообразии изучаемой совокупности. В обиходном понимании эксцесс еще рассматривается как всплеск, например ненормального поведения, или всплеск энергии, что отражается на характере кривой распределения. Во всяком случае, оценить нормальность изучаемых совокупностей можно уже при расчете эксцесса и коэффициента асимметрии.

Рис. Положительный и отрицательный эксцесс.

Для определения параметров и статистик мы практически использовали одну и ту же формулу, в которой изменялся номер порядковой степени у суммы отклонений значений от арифметического среднего. Здесь мы сталкиваемся с понятием момента. Моментами k-го порядка называют среднюю величину из k-степеней отклонений вариантов x от некоторой постоянной величины C.

L_k = (x_i – C)

Это понятие широко используется в механике, в виде моментов инерции, различают начальные, условные и центральные моменты. Начальным моментом называют момент в котором С = 0, условным моментом называют, когда C равно произвольной величине и момент называют центральным, когда С = χ. В качестве характеристик случайной величины и используют первый начальный момент, когда

L₁ = x_i – 0;

второй центральный момент, когда

L₂ = ∑(x_i – χ)².

Соответственно, как было показано выше третий и четвертый центральные моменты были использованы для определения коэффициента асимметрии и эксцесса.

Стандартизация переменных и таблицы плотности вероятности нормального распределения.

Закономерность распределения случайной величины (или случайной ошибки измерения), если распределение этой величины описывается нормальным законом распределения, достаточно хорошо изучена. Плотность вероятности нормального распределения определяют по формуле

φ(x) = [(1/σ)√2π]*e^{-(xi – μ)( xi – μ)/(2σ*σ)} .

Часто вместо переменной x_i используют нормированную переменную u, получаемую, используя следующее преобразование

u = (x_i – μ)/σ.

Это очень полезное преобразование, называемое стандартизацией. В результате стандартизации среднее становится равным нулю, а стандартное отклонение равным 1. В результате такого преобразования все значения переменной измеряются в единицах стандартного отклонения от -3 до +3, со средним равным 0. В результате стандартизации переменные, первоначально измеренные в каких-либо единицах измерения, таких как кг, футы, см, проценты и другие переходят во внутреннюю систему координат с нулевым средним и становятся безразмерными, при этом сохранив соотношение между цифрами, как до преобразования. Стандартизация позволяет вместе анализировать переменные, измеренные в разных единицах измерения. После подстановки в формулу Гаусса мы получаем формулу плотности вероятности более простого вида

φ(x) = [1/ √2π]*e^-(u*u)/2.

Плотности вероятности стандартного нормального распределения известны и давно рассчитаны, изданы таблицы, которые можно найти в любом учебнике по статистике и теории вероятности, в которых площади под кривой распределения прямо выражаются через вероятности.

Лекция 7

Рассмотрим пример.

На эксплуатационном блоке полиметаллического месторождения были отобраны пробы и получены данные, содержащиеся в таблице.

Данные были получены следующим образом. При подготовке блока к эксплуатации было пробурено 96 вертикальных скважин по квадратной сети 3.5 метра на 3.5 метра. Каждая скважина была опробована по интервалам (длина интервала -1 метр). Большое число равномерно расположенных в блоке проб позволило определить среднее содержание металла в блоке с большой точностью. Блок был разделен на 24 участка, в каждом из которых, оказалось, по 12 проб (4 скважины на 1 участок, 1 скважина содержит по 3 пробы). Общее количество проб равно 288 (24*12 = 288).

Содержание (%)	Частота	Относительная частота (частость)
0 – 0.5	59	0.205
0.5 -1	112	0.389
1 -1.5	64	0.202
1.5 – 2	18	0.062
2 – 2.5	12	0.042
2.5 – 3	8	0.028
3 – 3.5	5	0.017
3.5 – 4	5	0.017
4 – 4.5	2	0.007
4.5 – 5	1	0.004
5 – 5.5	2	0.007
Всего:	288	1.00

На рисунке приведено распределение содержания металла в 288 пробах.

Как видно на рисунке распределение носит асимметричный характер и явно не подчиняется нормальному закону.

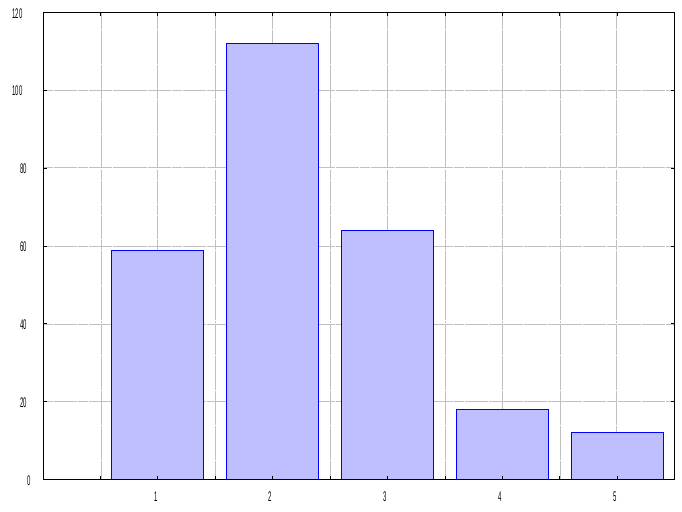
Рис. Гистограмма распределения полезного компонента в эксплуатационном блоке.

Затем было произведено 180 выборок из имеющихся анализов проб. В каждую выборку были случайным образом отобраны из каждого участка по одной пробе. Случайность отбора проб по участкам достигалась при помощи выбора свернутого листка с номером пробы из урны из общего количества свернутых листочков, равного количеству проб на участке. Для каждой выборки рассчитывалось среднее содержание металла, то есть в результате были получены 180 выборочных средних значений. Распределение выборочных средних значений по эксплуатационному блоку приведено в таблице и на рисунке.

Содержание (выборочное среднее)	Частота	Относительная частота (Частость)
0.7 – 0.8	3	0.017
0.8 – 0.9	13	0.072
0.9 – 1.0	30	0.167
1.0 – 1.1	40	0.222
1.1 – 1.2	41	0.228
1.2 – 1.3	31	0.172
1.3 – 1.4	16	0.089
1.4 – 1.5	5	0.028
1.5 – 1.6	1	0.005
Всего	180	1.0

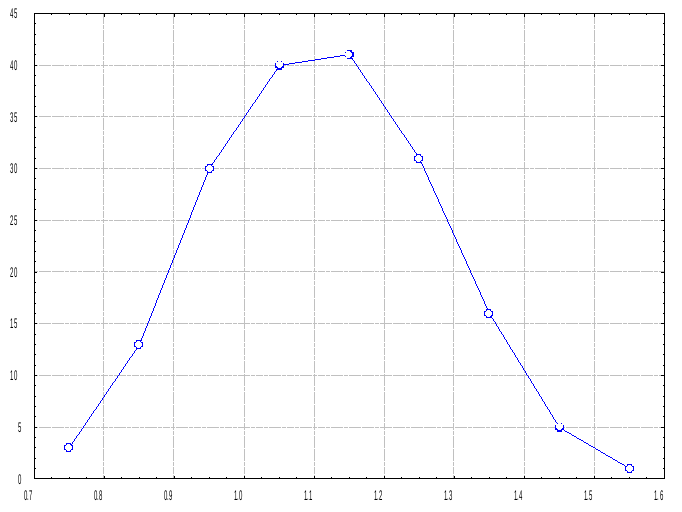
Рис. Распределение выборочного среднего значения по блоку.

Кривая распределения выборочного среднего значения похожа на колокол, причем среднеарифметическое всех выборочных средних значений равно 1.1, что соответствует среднему содержанию металла в блоке, которое как было уже указано выше, определено с большой точностью. Как видно из рисунка распределение выборочных средних значений соответствует или близко к нормальному распределению, хотя распределение просто полезного компонента имеет ярко выраженный асимметричный характер. Используя данные последней таблицы можно вычислить вероятность взятия пробы с некоторым содержанием или плотность вероятности, то есть вычислить вероятность взятия образца определенного класса. По данным второй таблицы вычисляем среднее и стандартное отклонение выборочных средних значений (χ = 1.11, а S = 0.159), а после для нижних границ по каждому интервалу вычисляем параметр u и получаем стандартизированные данные, у которых среднее арифметическое равно 0, а стандартное отклонение равно 1.

U₁ = (0.8 – 1.11)/0.159 = -1.95

Далее берем таблицы вероятности нормального распределения и для u₁ находим по таблице φ(x), в этом случае φ(x) = 0.026. Это также означает, что площадь части совокупности под кривой распределения, если смотреть по абсциссе, от минус бесконечности до значения u (u=-1.95), равна 0.026. Также вычисляем вероятности для класса, например для класса 0.8 – 0.9.

φ(0.8<x>0.9) = φ(u=-1.32) - φ(u=-1.95) = 0.093 – 0.026 = 0.067

То есть мы можем сказать, что с вероятностью 6.7% мы можем взять на месторождении пробу с содержанием от 0.8% до 0.9% данного металла.

Тот же самый результат мы получим, если расчеты будем делать не по таблице, а по формуле

φ(x) = [1/ √2π]*e^-(u*u)/2.

Если мы, используя формулу или таблицу вероятностей нормального распределения, рассчитаем вероятности для всех значений u, то увидим, что они близки к частостям последней таблицы по классам, из чего можно сделать вывод, что распределение наших эмпирических данных соответствует нормальному распределению.

Обычно мы не знаем, из какой совокупности мы берем выборку, но очень часто подозреваем, что изучаемая совокупность явно значительно отличается от нормальной совокупности. Эти подозрения обычно обусловлены сильно выраженными геологическими процессами, проявившимися на конкретном месторождении. Нужно отметить, все случайные величины, которые мы получаем в результате измерений, делятся на стохастические и детерминированные величины.

Стохастические случайные величины изучаемых признаков характерны для обычных спокойных, длительных во времени геологических и геохимических процессов. Обычно распределение стохастических величин подчиняется нормальному закону распределения.

Детерминированные величины возникают в результате определенных направленных процессов в земной коре, например приводящих к аномально высоким концентрациям химических элементов на локальных участках, которые потом нередко определяются геологами как промышленные скопления полезных компонентов. Теоретически детерминированные изменения природных объектов могут быть описаны средствами точных наук - физики, химии и математики, но практически тектонические и геохимические процессы в большей части очень сложны для понимания и описываются геологами на уровне гипотез. В большей части случаев стохастические, и детерминированные величины перемешаны между собой. Распределение этих перемешанных величин может подчиняться нормальному закону распределения, но больше всего распределения этих величин имеют ярко выраженный асимметричный характер.

Согласно классификации Пирсона можно выделить три типа данных, которые имеют три соответствующих типа распределений. К первому типу относятся данные, имеющие симметричное нормальное распределение, ко второму типу относятся данные, которые после математических преобразований будут иметь нормальное распределение и к третьему типу относятся данные, которые при любых преобразованиях не будут иметь нормальное распределение.