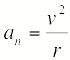1)Механическое движение. Элементы кинематики материальной точки: радиус-вектор, перемещение, скорость.

Механическим движением тела называется изменение его положения в пространстве относительно других тел с течением времени. Механическое движение тел изучает механика. Раздел механики, описывающий геометрические свойства движения без учета масс тел и действующих сил, называется кинематикой. Путь и перемещение. Линия, по которой движется точка тела, называется траекторией движения. Длина траектории называется пройденным путем. Вектор, соединяющий начальную и конечную точки траектории, называется перемещением. Движение тела, при котором все его точки в данный момент времени движутся одинаково, называется поступательным движением. Для описания поступательного движения тела достаточно выбрать одну точку и описать ее движение Движение, при котором траектории всех точек тела являются окружностями с центрами на одной прямой и все плоскости окружностей перпендикулярны этой прямой, называется вращательным движением

Материальная точка. Тело, размерами которого в данных условиях движения можно пренебречь, называют материальной точкой. Тело можно рассматривать как материальную точку, если его размеры малы по сравнению с расстоянием, которое оно проходит, или по сравнению с расстояниями от него до других тел. Космический корабль, пролетающий 8 км за 1 с, при наблюдении с поверхности Земли вполне можно рассматривать как материальную точку. Но космонавт, находящийся в космическом корабле, не может считать свой корабль материальной точкой. Когда траекторией движения материальной точки является прямая линия и направление движения не изменяется, модуль вектора перемещения равен пройденному пути. Если точка движется по криволинейной траектории, то модуль вектора перемещения меньше пройденного пути. Скорость. Для количественной характеристики процесса движения тела вводится понятие скорости движения. Мгновенной скоростью поступательного движения тела в момент времени t называется отношение очень малого перемещения к малому промежутку времени Δt , за который произошло это перемещение: Мгновенная скорость — векторная величина.

2) Ускорение точки. Нормальное и тангенциальное ускорения. Проекции ускорений на координатной оси.

Ускоре́ние (обычно обозначается , в теоретической механике ), производная скорости по времени — векторная величина, показывающая, насколько изменяется вектор скорости точки (тела) при её движении за единицу времени (т.е. ускорение учитывает не только изменение величины скорости, но и её направления)

При криволинейном движении скорость направлена по касательной к траектории. Поскольку направление скорости постоянно изменяется, то криволинейное движение - всегда движение с ускорением, в том числе, когда модуль скорости остается неизменным

В общем случае ускорение направлено под углом к скорости. Составляющая ускорения, направленная вдоль скорости, называется тангенциальным ускорением . Она характеризует изменение скорости по модулю.

Составляющая ускорения, направленная к центру кривизны траектории, т.е. перпендикулярно (нормально) скорости, называется нормальным ускорением . Она характеризует изменение скорости по направлению.

Здесь R - радиус кривизны траектории в данной точке. Тангенциальное и нормальное ускорение взаимноперпендикулярны, поэтому модуль полного ускорения

3)Кинематика вращательного движения. Угловая скорость и ускорение. Если в процессе движения абсолютно твердого тела (рис.2.1) его точки А и В остаются неподвижными, то и любая точка С тела, находящаяся на прямой АВ, также должна оставаться неподвижной. В противном случае расстояния АС и ВС должны были бы изменяться, что противоречило бы предположению об абсолютной твердости тела. Поэтому движение твердого тела, при котором две его точки Аи В остаются неподвижными, называют вращением тела вокруг неподвижной оси, а неподвижную прямую АВ называют осью вращения.

Рассмотрим произвольную точку М тела, не лежащую на оси вращения АВ. При вращении твердого тела расстояния М А и МВ и расстояние ρ точки М до оси вращения должны оставаться неизменными. Таким образом, все точки тела, вращающегося вокруг неподвижной оси, описывают окружности, центры которых лежат на оси вращения, а плоскости перпендикулярны этой оси. Движение абсолютно твердого тела, закрепленного в одной неподвижной точке, называют вращением тела вокруг неподвижной точки - центра вращения. Такое движение абсолютно твердого тела в каждый момент времени можно рассматривать как вращение вокруг некоторой оси, проходящей через центр вращения и называемой мгновенной осью вращения тела. Положение мгновенной оси относительно неподвижной системы отсчета и самого тела с течением времени может изменяться.

Углова́я ско́рость — векторная величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени: а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону. Углово́е ускоре́ние — псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела. При вращении тела вокруг неподвижной оси, угловое ускорение по модулю равно: Вектор углового ускорения α направлен вдоль оси вращения (в сторону при ускоренном вращении и противоположно  — при замедленном). При вращении вокруг неподвижной точки вектор углового ускорения определяется как первая производная от вектора угловой скорости ω по времени, то есть и направлен по касательной к годографу вектора в соответствующей его точке.